Условия оптимального распределения нагрузки между параллельно работающими блоками
Рассмотрим ТЭС (рис.1.14), на которой параллельно работает несколько блоков, каждый из которых состоит из парогенератора ПГ и турбины Т с генератором.
На рисунке n – число блоков, Bi(Pi) – расходная характеристика [т у.т./ч], P0 – общая нагрузка ТЭС. Необходимо определить такие мощности всех блоков Pi, при которых расход топлива на ТЭС будет минимальным. Составим математическую модель: вектор неизвестных целевая функция Ограничение определяется условием баланса мощности:
Составляем функцию Лагранжа:
условия экстремума которой
Множитель Лагранжа входит во все n условий, откуда Производная Оценим условия, при которых экстремум соответствует минимуму расхода топлива. Из математики известно, что при этом d2L > 0.
Таким образом, условие
обеспечивает минимум, если зависимости
Действительно, рассмотрим пример параллельной работы двух блоков с разными расходными характеристиками Bi(Pi) (рис.1.15). Полная нагрузка ТЭС P0 = 30 МВт. Рассмотрим 2 варианта распределения мощности по блокам: 1) Учитывая, что удельный расход для 1-го блока меньше, загрузим его по максимуму, приняв P1 = 20 МВт, P2 = 10 МВт. По характеристикам блоков определяем, что BS = 8 т у.т./ч. 2) Оценив при этом значения e, видим, что e1 ¹ e2; Равенство относительных приростов обеспечивается при P1 = 10 МВт и P2 = 20 МВт. По характеристикам блоков определяем, что в этом случае BS = 7 т у.т./ч. Условие равенства относительных приростов имеет четкий физический смысл.. Действительно, если имеем два блока с e1 ¹ e2 и e1 > e2, тогда первый блок можно разгрузить на DP. При этом получаем экономию Для сохранения баланса необходимо повысить P2 на ту же величину DP. Получается дополнительный расход топлива на втором блоке В результате получается реальная экономия топлива на ТЭС, равная
Рассмотрим случай, когда два блока однотипны и имеют одинаковые характеристики расхода топлива, но работают с разной мощностью. Характеристика относительного прироста (ХОП) показана на рис 1.16.
Поскольку
Разность приращений и определяет пережог
|


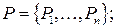
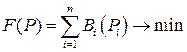 .
. .
.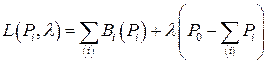 ;
; ,
,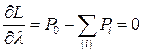 ;
; .
. , называемая относительным (удельным) приростом расхода топлива характеризует изменение расхода топлива при изменении мощности на 1 МВт в течении часа. Измеряется прирост в т у.т./МВт*ч.
, называемая относительным (удельным) приростом расхода топлива характеризует изменение расхода топлива при изменении мощности на 1 МВт в течении часа. Измеряется прирост в т у.т./МВт*ч.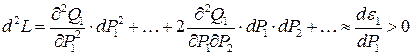 ;
;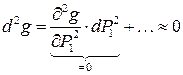 ;
;
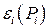 являются возрастающими.
являются возрастающими. При распределении нагрузки учитываются относительные приросты, а не удельные расходы, определяемые в т у.т. на 1 МВт*ч произведенной энергии.
При распределении нагрузки учитываются относительные приросты, а не удельные расходы, определяемые в т у.т. на 1 МВт*ч произведенной энергии.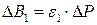 .
. .
.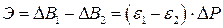 .
. В оптимальном режиме нагрузка каждого блока Ро. Оценим пережог топлива при работе блоков с нагрузкой Р1 и Р2.
В оптимальном режиме нагрузка каждого блока Ро. Оценим пережог топлива при работе блоков с нагрузкой Р1 и Р2.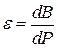 , то любое приращение расхода топлива
, то любое приращение расхода топлива пропорционально соответствующей площади.
пропорционально соответствующей площади.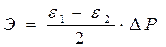 .
.


