Выбор оптимального аварийного резерва
Под расчетным аварийным резервом понимают разность между располагаемой мощностью включенного в работу генерирующего оборудования и спросом
Обе составляющие меняются под воздействием независимых случайных событий, причем Для математического анализа непрерывный случайные процесс представляется как дискретный. Величина дискретной ступени В этом случае можно рассмотреть два следующих дискретных ряда: ряд вероятностей аварийного снижения генерации в котором нижний индекс определяет величину аварийного выхода, и ряд вероятности снижения нагрузки относительно максимальной
Перемножим оба ряда:
Произведение будет состоять из суммы двух сомножителей, каждая из которых определяет вероятность сложного события, а сумма нижних индексов определяет соответствующий событию дефицит мощности. Например, слагаемое Таким образом, если в часы максимума нагрузки нет резерва(R=0), то по сумме нижних индексов можно определить вероятность любого дефицита в ke МВтпутем выбора из произведения рядов соответствующих слагаемых
Если в часы максимума нагрузки есть резерв, равный R=re, то
Ущерб у потребителей от недоотпуска электроэнергии за время T:
Введем понятие интегральной вероятности дефицита в e МВт, как суммы вероятностей рассматриваемого дефицита и всех больших по величине дефицитов в 2e, 3e и т.д.
В этом случае ущерб определяется как Определим целесообразность повышения резерва на величину e МВт до значения при этом снизится ущерб на величину
Увеличение резерва будет выгодно, когда т.е. при выполнении условия или Ниже на рис. 1.49 приводится блок-схема алгоритма выбора оптимального резерва. 1. Ввод исходной информации; 2. RДОП = 0; 3. У(0) = 0; 4. Определение ряда снижения нагрузок 5. Определение членов дискретного ряда 6. Расчет 7. Определение 8. Определение ущерба 9. Проверка условия 10. Печать RДОП; 11. Увеличение резерва 12.
|

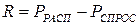 .
. – дискретно, пропорционально номинальной мощности аварийно отключаемых блоков, а
– дискретно, пропорционально номинальной мощности аварийно отключаемых блоков, а 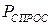 – непрерывно.
– непрерывно.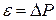 принимается равной мощности минимального блока системы.
принимается равной мощности минимального блока системы.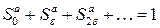 ,
, , где нижний индекс определяет отклонение нагрузки от максимальной.
, где нижний индекс определяет отклонение нагрузки от максимальной.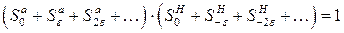 .
.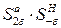 определяет вероятность аварийного выхода 2 e при снижении нагрузки на e, где2 e - e = e определяет дефицит при отсутствии резерва в часы наибольшей нагрузки.
определяет вероятность аварийного выхода 2 e при снижении нагрузки на e, где2 e - e = e определяет дефицит при отсутствии резерва в часы наибольшей нагрузки.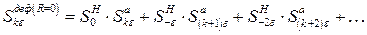
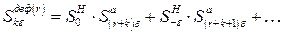
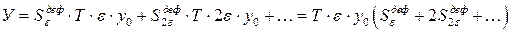
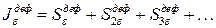 ,
,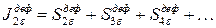 ,
,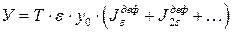 .
. . Это изменение резерва и состава блоков приведет к тому, что изменятся интегральные вероятности дефицитов, и
. Это изменение резерва и состава блоков приведет к тому, что изменятся интегральные вероятности дефицитов, и
 Так как
Так как 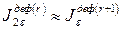 ,
,  , …, то они компенсируют друг друга и снижение ущерба составит
, …, то они компенсируют друг друга и снижение ущерба составит  .
.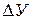 превысит затраты на увеличение резерва, равные
превысит затраты на увеличение резерва, равные  ,
, ,
,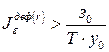 .
.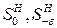 , …;
, …; , …;
, …;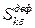 , k = 1,2…;
, k = 1,2…;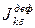 , k = 1,2…;
, k = 1,2…;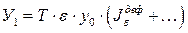 ;
;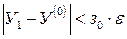 ;
; ;
;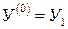 .
.


