ВАЛЫ И ОСИ
ВАЛЫ И ОСИ
Колёса передач установлены на специальных продолговатых деталях круглого сечения. Среди таких деталей различают оси и валы [7,11,38]. Ось – деталь, служащая для удержания колёс и центрирования их вращения. Вал – ось, передающая вращающий момент. Не следует путать понятия "ось колеса", это деталь и "ось вращения", это геометрическая линия центров вращения.
Форма вала определяется распределением изгибающих и крутящих моментов по его длине. Правильно спроектированный вал представляет собой балку равного сопротивления.
Валы и оси вращаются, а следовательно, испытывают знакопеременные нагрузки, напряжения и деформации. Поэтому поломки валов и осей имеют усталостный характер.
Причины поломок валов и осей прослеживаются на всех этапах их "жизни". 1. На стадии проектирования – неверный выбор формы, неверная оценка концентраторов напряжений. 2. На стадии изготовления – надрезы, забоины, вмятины от небрежного обращения. 3. На стадии эксплуатации – неверная регулировка подшипниковых узлов. Для работоспособности вала или оси необходимо обеспечить: è объёмную прочность (способность сопротивляться Mизг и Мкрут); è поверхностную прочность (особенно в местах соединения с другими деталями); è жёсткость на изгиб; è крутильную жёсткость (особенно для длинных валов). Все валы в обязательном порядке рассчитывают на объёмную прочность. Схемы нагружения валов и осей зависят от количества и места установки на них вращающихся деталей и направления действия сил. При сложном нагружении выбирают две ортогональные плоскости (например, фронтальную и горизонтальную) и рассматривают схему в каждой плоскости. Рассчитываются, конечно, не реальные конструкции, а упрощённые расчётные модели, представляющие собой балки на шарнирных опорах, балки с заделкой и даже статически неопределимые задачи [7]. При составлении расчётной схемы валы рассматривают как прямые брусья, лежащие на шарнирных опорах. При выборе типа опоры полагают, что деформации валов малы и, если подшипник допускает хотя бы небольшой наклон или перемещение цапфы, его считают шарнирно-неподвижной или шарнирно-подвижной опорой. Подшипники скольжения или качения, воспринимающие одновременно радиальные и осевые усилия, рассматривают как шарнирно-неподвижные опоры, а подшипники, воспринимающие только радиальные усилия, - как шарнирно-подвижные. Такие задачи хорошо известны студентам из курсов теоретической механики (статики) и сопротивления материалов. Расчёт вала на объёмную прочность выполняют в три этапа.
I. Предварительный расчёт валов Выполняется на стадии проработки Технического Задания, когда известны только вращающие моменты на всех валах машины. При этом считается, что вал испытывает только касательные напряжения кручения tкр = Мвр / Wp £ [ t ] кр, где Wp - полярный момент сопротивления сечения. Для круглого сечения: Wp = pd3/16, [ t ] кр= 15 ¸; 20 Н/мм2. Условие прочности по напряжениям кручения удобно решать относительно диаметра вала
Это – минимальный диаметр вала. На всех других участках вала он может быть только больше. Вычисленный минимальный диаметр вала округляется до ближайшего большего из нормального ряда. Этот диаметр является исходным для дальнейшего проектирования.
II. Уточнённый расчёт валов На данном этапе учитывает не только вращающий, но и изгибающие моменты. Выполняется на этапе эскизной компоновки, когда предварительно выбраны подшипники, известна длина всех участков вала, известно положение всех колёс на валу, рассчитаны силы, действующие на вал. Чертятся расчётные схемы вала в двух плоскостях. По известным силам в зубчатых передачах и расстояниям до опор строятся эпюры изгибающих моментов в горизонтальной и фронтальной плоскостях. Затем вычисляется суммарный изгибающий момент
Далее рассчитывается и строится эпюра эквивалентного "изгибающе-вращающего" момента
где α = 0,75 или 1 в зависимости от принятой энергетической теории прочности [5], принимаемый большинством авторов равным 1. Вычисляется эквивалентное напряжение от совместного действия изгиба и кручения s экв = Мэкв / Wp. Уравнение также решается относительно минимального диаметра вала
Или то же самое для сравнения с допускаемыми нормальными напряжениями:
Полученный в уточнённом расчёте минимальный диаметр вала принимается окончательно для дальнейшего проектирования.
III. Расчёт вала на выносливость Выполняется как проверочный на стадии рабочего проектирования, когда практически готов рабочий чертёж вала, т.е. известна его точная форма, размеры и все концентраторы напряжений: шпоночные пазы, кольцевые канавки, сквозные и глухие отверстия, посадки с натягом, галтели (плавные, скруглённые переходы диаметров). При расчёте полагается, что напряжения изгиба изменяются по симметричному циклу, а касательные напряжения кручения – по отнулевому пульсирующему циклу. Проверочный расчёт вала на выносливость по существу сводится к определению фактического коэффициента запаса прочности n, который сравнивается с допускаемым
Здесь ns и nt - коэффициенты запаса по нормальным и касательным напряжениям
где s -1 и τ-1 – пределы выносливости материала вала при изгибе и кручении с симметричным циклом; kσ и kτ – эффективные коэффициенты концентрации напряжений при изгибе и кручении, учитывающие галтели, шпоночные канавки, прессовые посадки и резьбу; εα и ετ – масштабные коэффициенты диаметра вала; s a и τa – амплитудные значения напряжений; s m и τm – средние напряжения цикла (s m = 0, τm = τa); ψσ и ψτ – коэффициенты влияния среднего напряжения цикла на усталостную прочность зависят от типа стали. Вычисление коэффициентов запаса прочности по напряжениям подробно излагалось в курсе "Сопротивление материалов", в разделе "Циклическое напряжённое состояние". Если коэффициент запаса оказывается меньше требуемого, то сопротивление усталости можно существенно повысить, применив поверхностное упрочнение: азотирование, поверхностную закалку токами высокой частоты, дробеструйный наклёп, обкатку роликами и т.д. При этом можно получить увеличение предела выносливости до 50% и более.
КОНТРОЛЬНЫЕ ВОПРОСЫ s Чем различаются валы и оси? s Какой динамический характер имеют напряжения изгиба в валах и осях? s Каковы причины поломок валов и осей? s В каком порядке выполняются этапы прочностного расчёта валов? s Какой диаметр определяется в проектировочном расчёте валов?
|

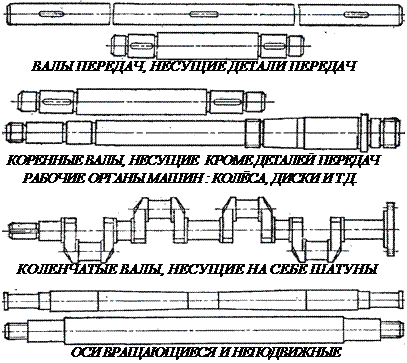 Формы валов и осей весьма многообразны от простейших цилиндров до сложных коленчатых конструкций. Известны конструкции гибких валов, которые предложил шведский инженер Карл де Лаваль ещё в 1889 г.
Формы валов и осей весьма многообразны от простейших цилиндров до сложных коленчатых конструкций. Известны конструкции гибких валов, которые предложил шведский инженер Карл де Лаваль ещё в 1889 г.
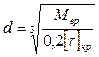 .
.









