Уравнение движения одиночного экипажа.
КОНСПЕКТ ЛЕКЦІЙ З ДИСЦИПЛІНИ «ПЕРЕТВОРЮВАЛЬНА ТЕХНІКА» ДЛЯ СПЕЦІАЛІСТІВ СПЕЦІАЛЬНОСТІ 7.090603 «Електротехнічні системи електроспоживання»
Укладачі: Микола Степанович Путілін Андрій Олександрович Бойко
Уравнение движения поезда. Уравнение движения одиночного экипажа.
Предположим, что к экипажу приложена сумма сил, причем равнодействующая этих сил F направлена по линии, проходящей через центр тяжести тела параллельно горизонтальной плоскости. В этом случае, согласно II закону Ньютона, экипаж начнет двигаться с постоянным ускорением а. Но в чистом виде II закон Ньютона в данном случае применять нельзя, т.к. экипаж имеет вращающиеся части. Кинетическая энергия экипажа, движущегося по горизонтальной плоскости
где J – момент инерции вращающихся частей; w – угловая частота вращения колес, имеющих радиус R. Выразим угловую частоту вращения колес через линейную скорость движения экипажа:
Для того, чтобы размерность обоих слагаемых выражения совпадала, необходимо, чтобы отношение
Отношение
То есть коэффициент инерции вращающихся частей показывает, насколько увеличивается кинетическая энергия экипажа (поезда) за счет наличия в нем вращающихся частей. Следует отметить, что полученное определение справедливо только для тех вращающихся частей, вращение которых зависит от поступательного движения. Так, коэффициент инерции вращающихся частей электровоза не учитывает инерционность вентиляторов принудительного охлаждения тяговых двигателей, а также инерционность других вспомогательных машин. В литературе можно встретить термин эквивалентная масса mэ – это фиктивная масса, которой должно обладать тело без вращающихся частей, но обладающее такой же кинетической энергией, что и тело массой m, но имеющее вращающиеся части: mэ = m × (1 + g). Кинетическая энергия экипажа в процессе движения под воздействием силы F будет изменяться. Это изменение равно работе, совершаемой равнодействующей сил на каком либо отрезке пути. Предположим, что экипаж переместился на расстояние ds. При этом скорость движения увеличится на dV, а кинетическая энергия – на dAк. Продифференцируем выражение для кинетической энергии по скорости:
Таким образом, dAк = m × (1 + g) × V × dV. Выразим величину приращения кинетической энергии через работу силы F и приравняем оба выражения: dAк = F × ds = m × (1 + g) × V × dV. Отсюда
Учитывая, что
можно записать
Полученные выражения являются двумя формами уравнения движения экипажа. Из выражений следует, что интегрировать уравнение движения возможно по скорости, пути и времени. На практике, для удобства, используют уравнение движения в удельных величинах. Для получения такой разновидности уравнения разделим правую и левую части на массу:
Здесь f – удельная равнодействующая сил, то есть сила, приходящаяся на 1 т массы поезда. Помимо физической системы единиц, существует еще и техническая (железнодорожная), которая сложилась исторически по мере развития науки о тяге поездов. В этой системе вместо массы фигурирует вес. Учитывая, что Q = m×g, можно записать
Обозначив
получим
Здесь z – коэффициент, соответствующий ускорению поезда в км/ч2 с учетом инерции вращающихся частей при действии на него единичной удельной ускоряющей силы. Обозначается греческой буквой "дзета".
|

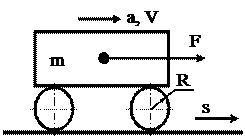 Для вывода уравнения движения рассмотрим энергетику движения простейшего экипажа массой m по горизонтальной плоскости.
Для вывода уравнения движения рассмотрим энергетику движения простейшего экипажа массой m по горизонтальной плоскости. ,
,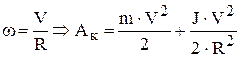 .
. имело размерность [кг]. Обозначим это отношение как некую фиктивную массу вращения mв. Тогда:
имело размерность [кг]. Обозначим это отношение как некую фиктивную массу вращения mв. Тогда: .
. принято называть коэффициентом инерции вращающихся частей и обозначать буквой g. С учетом вышесказанного
принято называть коэффициентом инерции вращающихся частей и обозначать буквой g. С учетом вышесказанного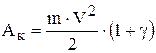 .
. .
. .
. ,
, .
. .
. ;
;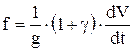 .
.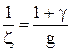 ,
, .
.


