Перераспределение сил взаимодействия колеса и рельса под действием вращающего момента.
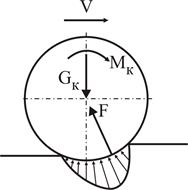
Предположим, что поверхность колеса и рельса состоит из микрочастиц, которые связаны между собой упругими связями и имеют возможность перемещаться по поверхности. При отсутствии вращающего момента частицы равномерно распределены по поверхности колеса и рельса. Под действием вращающего момента колесо начинает испытывать упругий подпор со стороны рельса, который схематично представлен равнодействующей силой F и условным возвышением уровня рельса в направлении движения. Вследствие смещения точки приложения силы реакции со стороны колеса происходит перераспределение напряжений в материале колеса и область, в которой давление выше предела упругости смещается по направлению вращения колеса.
Таким образом, создается эффект перемещения микрочастиц колеса по его поверхности при переходе частиц за пределы заштрихованной области. Перемещение происходит в направлении, противоположном движению центра вращения колеса. Предположим, что колесо повернулось на элементарный угол da. В случае недеформированного колеса перемещение его центра будет равно: dxa = R × da. Но, т.к. перемещение микрочастиц колеса по его поверхности, вызванное упругими деформациями, направлено навстречу перемещению центра колеса, то действительное перемещение центра колеса будет меньше на величину относительного перемещения микрочастиц по его поверхности: dx = dxa – du. Это явление называют упругим скольжением. В иностранной литературе оно носит название крипа (ползучести). Из полученного выражения следует, что в режиме тяги действительный путь, проходимый центром колеса меньше пути, подсчитанного по угловой скорости и геометрическому радиусу (dx < R × da) – колесо как бы проскальзывает относительно рельса. Если сделать аналогичные выкладки для режима торможения – получим обратный результат: путь, проходимый центром колеса больше пути, подсчитанного по угловой скорости.
|

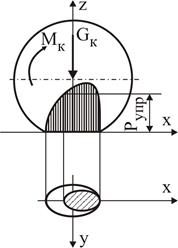 Вследствие значительных усилий от давления колеса на рельс в этой области частицы материала колеса не могут перемещаться относительно частиц материала рельса (сцепляются друг с другом). В пределах заштрихованной области наблюдается избыток частиц материала колеса. Вне заштрихованной области усилия от давления колеса меньше, частицы материала колеса имеют возможность перемещаться относительно частиц материала рельса и стремятся вновь равномерно распределиться по поверхности колеса.
Вследствие значительных усилий от давления колеса на рельс в этой области частицы материала колеса не могут перемещаться относительно частиц материала рельса (сцепляются друг с другом). В пределах заштрихованной области наблюдается избыток частиц материала колеса. Вне заштрихованной области усилия от давления колеса меньше, частицы материала колеса имеют возможность перемещаться относительно частиц материала рельса и стремятся вновь равномерно распределиться по поверхности колеса.


