Основные положения. Основная идея резонансных методов состоит в наблюдении резонансных кривых колебательного контура, в который введён образец исследуемого диэлектрика
Лабораторная работа
Основная идея резонансных методов состоит в наблюдении резонансных кривых колебательного контура, в который введён образец исследуемого диэлектрика. Изучение резонансных кривых до и после внесения диэлектрика позволяет по добротности контура и его резонансной частоте определить диэлектрическую проницаемость и тангенс угла диэлектрических потерь образца. При работе в СВЧ-диапазоне применяются объёмные резонаторы, например коаксиальный резонатор с торцевым зазором (рис. 1). Если диаметр центрального проводника
Измерение частотных характеристик коэффициента передачи
Извлечение параметров материала. Диэлектрические параметры исследуемых материалов извлекаются из измеренных ранее частотных зависимостей коэффициента передачи Положения максимумов на кривых Для пустого резонатора емкость зазора между центральным проводником и торцевым основанием определяется как
где
Отсюда можно найти Для резонатора с образцом ёмкость зазора будет определяться как:
(где
Используя предыдущие формулы, можно получить диэлектрическую проницаемость образца:
Добротности пустого резонатора
Тангенс угла диэлектрических потерь материала образца рассчитывается по формуле
где
|

 и ширина зазора h оказываются значительно меньше длины волны, то ёмкость можно считать сосредоточенной в зазоре между центральным проводником и торцевым основанием резонатора. На рис. 1:
и ширина зазора h оказываются значительно меньше длины волны, то ёмкость можно считать сосредоточенной в зазоре между центральным проводником и торцевым основанием резонатора. На рис. 1:  ,
, 
 . Блок-схема резонансного метода измерений представлена на рис. 2. Исследуемый образец устанавливается в торец коаксиального резонатора (ширина зазора регулируется по размеру образца).
. Блок-схема резонансного метода измерений представлена на рис. 2. Исследуемый образец устанавливается в торец коаксиального резонатора (ширина зазора регулируется по размеру образца). Рис. 2
Рис. 2
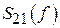 .
.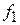 или резонатора с образцом
или резонатора с образцом  .
. ,
, и
и  ,
, и
и  .
. .
.
 – диэлектрическая проницаемость материала образца);
– диэлектрическая проницаемость материала образца); ,
,  .
. .
. и резонатора с образцом
и резонатора с образцом  будут определяться выражениями:
будут определяться выражениями: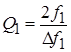 и
и  .
. ,
, ,
,  .
.


