Процесс ортогонализации системы векторов.
1. Сначала про проекцию одного вектора на ось, задаваемую другим вектором. Проекция вектора на ось – это не вектор, это - ЧИСЛО, но число со знаком (или нуль, если вектор перпендикулярен оси).
Например, пусть ось направлена вдоль вектора 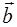 , и нам надо найти проекцию на эту ось некоторого вектора
, и нам надо найти проекцию на эту ось некоторого вектора  (см. картинку). Если угол между векторами равен
(см. картинку). Если угол между векторами равен 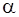 , то
, то 
 =
=  . Составляющая же вектора
. Составляющая же вектора  , направленная вдоль вектора
, направленная вдоль вектора 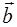 - это уже вектор, и равен он
- это уже вектор, и равен он  . Итого, эта составляющая равна
. Итого, эта составляющая равна 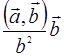 .
.
Вычтем из вектора  его составляющую вдоль
его составляющую вдоль 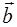 . Получится вектор
. Получится вектор  Докажите, что получившийся вектор
Докажите, что получившийся вектор  перпендикулярен вектору
перпендикулярен вектору 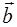 . (Подсказка: найдите их скалярное произведение. Равенство его нулю и есть признак перпендикулярности. Используйте тот факт, что
. (Подсказка: найдите их скалярное произведение. Равенство его нулю и есть признак перпендикулярности. Используйте тот факт, что  )
)
2. Пусть даны три линейно независимых вектора  в трехмерном пространстве. (Помните, как проверить, что они линейно независимы и потому образуют базис?). Надо провести процесс ортогонализации, начиная с какого-нибудь вектора. Предположим, с первого. То есть надо предъявить три новых, уже взаимно перпендикулярных вектора
в трехмерном пространстве. (Помните, как проверить, что они линейно независимы и потому образуют базис?). Надо провести процесс ортогонализации, начиная с какого-нибудь вектора. Предположим, с первого. То есть надо предъявить три новых, уже взаимно перпендикулярных вектора  , первый из которых и есть сам
, первый из которых и есть сам  :
:
 .
.
Второй вектор,  , найдем, вычтя из
, найдем, вычтя из  его составляющую вдоль
его составляющую вдоль  :
:
 .
.
Получили уже два взаимно перпендикулярных вектора -  и
и  . Идём дальше.
. Идём дальше.
Третий вектор,  , найдем, вычтя из
, найдем, вычтя из  его составляющие вдоль найденных векторов - и вдоль
его составляющие вдоль найденных векторов - и вдоль  , и вдоль
, и вдоль  :
:
 .
.
Докажите, что вектор  перпендикулярен и
перпендикулярен и  , и
, и  . (Используйте, что
. (Используйте, что  , они же взаимно перпендикулярны!)
, они же взаимно перпендикулярны!)

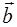 , и нам надо найти проекцию на эту ось некоторого вектора
, и нам надо найти проекцию на эту ось некоторого вектора  (см. картинку). Если угол между векторами равен
(см. картинку). Если угол между векторами равен 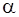 , то
, то 
 =
=  . Составляющая же вектора
. Составляющая же вектора  . Итого, эта составляющая равна
. Итого, эта составляющая равна 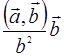 .
. Докажите, что получившийся вектор
Докажите, что получившийся вектор  перпендикулярен вектору
перпендикулярен вектору  )
) в трехмерном пространстве. (Помните, как проверить, что они линейно независимы и потому образуют базис?). Надо провести процесс ортогонализации, начиная с какого-нибудь вектора. Предположим, с первого. То есть надо предъявить три новых, уже взаимно перпендикулярных вектора
в трехмерном пространстве. (Помните, как проверить, что они линейно независимы и потому образуют базис?). Надо провести процесс ортогонализации, начиная с какого-нибудь вектора. Предположим, с первого. То есть надо предъявить три новых, уже взаимно перпендикулярных вектора  , первый из которых и есть сам
, первый из которых и есть сам  :
: .
. , найдем, вычтя из
, найдем, вычтя из  его составляющую вдоль
его составляющую вдоль  .
. и
и  , найдем, вычтя из
, найдем, вычтя из  его составляющие вдоль найденных векторов - и вдоль
его составляющие вдоль найденных векторов - и вдоль  .
. , они же взаимно перпендикулярны!)
, они же взаимно перпендикулярны!)


