СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Vacance (f): вакансия, вакантное место. Vacances (f, pl) (scolaires): каникулы. Vacataire: временный, внештатныйработник; почасовик. Validation (d'un diplôme): утверждение, признание (диплома) действительным.
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Теория систем линейных алгебраических уравнений является одним из основных разделов линейной алгебры. Нет такой отрасли науки и приложений, где в том или ином виде она не использовались бы. Хотя общая теория систем линейных алгебраических уравнений и была завершена к концу XIX века, исследования в этой области продолжаются до сих пор. Они стали более чем актуальными в связи с применением в исследованиях электронных вычислительных средств и необходимостью экстраполировать различные задачи со многими параметрами в физике, космонавтике, теории кодирования, некоторых разделах математики и т.д. Представляет большой практический интерес построение алгоритмов получения решений систем с минимальной допустимой погрешностью и минимальной вычислительной трудоемкостью. Таким образом, вполне вероятно, что новые практические и теоретические задачи выдвинут новые проблемы перед старейшим разделом математики – теорией систем линейных алгебраических уравнений.
Вопрос 1. Понятие системы n линейных уравнений с n неизвестными О. 1.1. Системой n уравнений с n неизвестными называется множество уравнений вида
где О.1.2. Уравнение вида
О. 1.3. Система уравнений вида
называется системой n линейных уравнений с n неизвестными, где Система линейных уравнений (1) называется квадратной, так как у нее число уравнений совпадает с числом неизвестных. О.1.4. Решением системы (1) называется такая совокупность чисел ( О.1.5. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет. О.1.6. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением. Т.1.1. Если система линейных уравнений (СЛУ) имеет более одного решения, то она имеет бесконечное множество решений.
Следовательно, неопределенная СЛУ имеет бесконечное множество решений. Решить СЛУ – это значит выяснить, совместна она или нет. Если СЛУ совместна, найти ее общее решение. О. 1.7. Две системы линейных уравнений называются равносильными или эквивалентными, если они имеют одно и тоже множество решений.
Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы, к которым относятся: 1. перестановка уравнений; 2. умножение обеих частей одного из уравнений на число, отличное от нуля; 3. умножение какого-либо уравнения на число и прибавление его к другому уравнению.
Если в результате элементарных преобразований системы появилось уравнение вида
которое называется тривиальным, то его можно вычеркнуть, так как оно не влияет на решение системы. Если в результате элементарных преобразований системы появилось уравнение вида
которое называется противоречивым, то такая СЛУ является несовместной, т.е. решений не имеет.
Вопрос 2. Матричный метод решения систем
Рассмотрим методы решения квадратных СЛУ. Пусть дана СЛУ (1). Введем матрицы:
Тогда СЛУ (1) можно записать в матричной форме: АХ = В. (2) Основная матрица системы (1), т.е. матрица А, является квадратной матрицей n-го порядка. Пусть
Отсюда получим решение матричного уравнения (2):
Отыскание решения системы (1) по формуле (3) называется матричным методом решения системы. Формула (3) дает единственное решение системы (1) в случае невырожденности матрицы А, т.е. при Замечание. Если основная матрица А системы (1) вырожденна, т.е. Пример 1. Решить СЛУ матричным методом: Решение
1. 2.
Ответ: (1, 1, 1)
Вопрос 3. Теорема Крамера Решение СЛУ (1) удобно записывать и вычислять с помощью определителей. Имеет место теорема: Т.3.1. (Теорема Крамера) Если определитель системы (1) nлинейных уравнений с nнеизвестными отличен от нуля, то система (1) совместна и имеет единственное решение, определяемое по формулам:
где Формулы (4) называются формулами Крамера. Замечание. Если основная матрица А системы (1) вырожденна, т.е. 1) хотя бы один из определителей 2) все определители Пример 2. 1. 2. 3. Замечание. Матричный метод и теорема Крамера могут быть использованы для решения только квадратных СЛУ, у которых число уравнений равно числу неизвестных. Пример 3. Решить систему из примера 1 по правилу Крамера. Решение 1. 2. 3. Ответ: (1, 1, 1)
Существенным недостатком решения СЛУ по формулам Крамера и матричным методом является их большая трудоемкость, связанная с вычислением определителей и нахождением обратных матриц. Поэтому эти методы представляют больше теоретический интерес. Вопрос 4. Понятие системы m линейных уравнений с n неизвестными. Теорема Кронекера-Капелли
В общем случае система mлинейных уравнений с nнеизвестными имеет вид:
Системе (5) можно сопоставить две матрицы: А =
Матрица А состоит из коэффициентов при неизвестных, а матрица Эти матрицы играют важную роль в вопросе разрешимости СЛУ. Исчерпывающий ответ на вопрос о разрешимости СЛУ (5) дает теорема Кронекера-Капелли. Т.4.1. ( т еорема Кронекера – Капелли, критерий совместности СЛУ) Система линейных уравнений (5)совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы, т. е. Пример 4. Исследовать на совместность систему Решение
О.4.1. Рангом совместной СЛУ называется ранг ее матрицы.
Правила практического разыскания всех решений совместной СЛУ вытекают из следующих теорем.
|



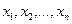 - неизвестные,
- неизвестные,  - свободные члены,
- свободные члены,  - функции, определяющие зависимость между неизвестными.
- функции, определяющие зависимость между неизвестными. , где
, где  - некоторые числа, называется линейным относительно неизвестных
- некоторые числа, называется линейным относительно неизвестных  (1)
(1) - коэффициенты системы (1),
- коэффициенты системы (1),  - свободные члены.
- свободные члены. ), при подстановке которых все уравнения системы обращаются в верные равенства.
), при подстановке которых все уравнения системы обращаются в верные равенства.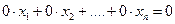 ,
,
 - матрица коэффициентов системы (основная матрицы);
- матрица коэффициентов системы (основная матрицы);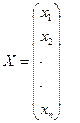 - столбец неизвестных;
- столбец неизвестных;  - столбец свободных членов.
- столбец свободных членов. , тогда существует обратная матрица
, тогда существует обратная матрица 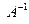 . Умножим обе части матричного равенства (2) на
. Умножим обе части матричного равенства (2) на 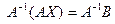 ,
,  ,
,  .
. . (3)
. (3)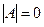 , то обратная матрица
, то обратная матрица 

 Þ СЛУ совместна и определена.
Þ СЛУ совместна и определена.



 =
= 
 , (4)
, (4) - определитель основной матрицы СЛУ (1);
- определитель основной матрицы СЛУ (1);  - определитель, полученный из
- определитель, полученный из  ).
). , то возможны два случая:
, то возможны два случая: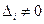 . В этом случае СЛУ (1)несовместна.
. В этом случае СЛУ (1)несовместна. . В этом случае о совместности СЛУ (1) ничего нельзя сказать.
. В этом случае о совместности СЛУ (1) ничего нельзя сказать. Þ
Þ 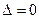 ,
,  - СЛУ несовместна.
- СЛУ несовместна. Þ
Þ  - СЛУ имеет множество решений.
- СЛУ имеет множество решений. Þ
Þ  ;
;  ;
;  .
.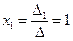 ,
,  ,
,  .
. . (5)
. (5) - основная матрица системы (5);
- основная матрица системы (5); - расширенная матрица системы (5).
- расширенная матрица системы (5). дополнена ещё столбцом свободных членов.
дополнена ещё столбцом свободных членов.
 .
. ~
~  Þ
Þ 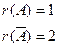 Þ
Þ  Þ система несовместна.
Þ система несовместна.


