Правило решения произвольной системы линейных уравнений
4. Придавая свободным неизвестным любые числовые значения, получают соответствующие значения главных неизвестных. Т.о. можно найти частные решения исходной системы. Пример 5. Решить систему Решение 1. Исследуем систему на совместность:
~ Вывод: СЛУ совместна и определена (имеет единственное решение). 2. Выберем первые три уравнения, из коэффициентов которых составим базисный минор:
3. Найдем решение по формулам Крамера:
Отсюда получим Ответ: (1, 2, 1).
Пример 6. Решить систему Решение 1. Исследуем систему на совместность:
~ Вывод: Так как 2. Берем первые два уравнения системы:
В базисный минор вошли коэффициенты при неизвестные
3. Найдем общее решение по формулам Крамера:
Отсюда получим Общее решение: ( 4. Найдем частное решение при Тогда Частное решение: (-1, 1, 0, 1). Одним из наиболее эффективных и универсальных методов решения СЛУ является метод Жордана-Гаусса, состоящий в последовательном исключении неизвестных. Вопрос 5. Метод Жордана – Гаусса.
Пусть дана произвольная СЛУ (5): Рассмотрим расширенную матрицу системы (1): Используя элементарные преобразования матриц, выполняемые над строками, приведем матрицу Будем считать, что элемент Разделив первую строку матрицы Для получения нулей в первом столбце (исключение неизвестного
где Разделив теперь элементы второй строки на
Продолжая процесс последовательного исключения неизвестных, получим равносильную матрицу вида 1. Если r = n, то матрица (6) имеет вид
В этом случае СЛУ (1) имеет единственное решение 2. Если r < n, то СЛУ (5) имеет множество решений, причем неизвестные
3. Если в результате преобразований матрицы Пример 7. Решить систему Решение
~ Ответ: (1, 2, 1). Пример 8. Решить систему Решение
~ ~ Пусть
Общее решение: (
Пример 9. Решить систему Решение
Вывод: система несовместна.
|

 . Если
. Если  , то система несовместна. Если
, то система несовместна. Если  , то система совместна, и необходимо найти какой-либо базисный минор порядка r (т.е. отличный от нуля минор, порядок которого равен рангу системы).
, то система совместна, и необходимо найти какой-либо базисный минор порядка r (т.е. отличный от нуля минор, порядок которого равен рангу системы).  неизвестных называют свободными и переносят в правые части уравнений.
неизвестных называют свободными и переносят в правые части уравнений.  .
. ~
~ 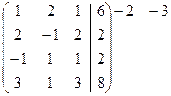 ~
~  ~
~  ~
~ Þ
Þ  Þ
Þ  - базисный минор.
- базисный минор. ,
,  ,
,  .
. ,
,  ,
,  .
. .
. ~
~  ~
~  ~
~ ~
~  .
. Þ
Þ 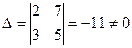 - базисный минор.
- базисный минор. ,
,  - число главных неизвестных,
- число главных неизвестных,  - число свободных неизвестных.
- число свободных неизвестных. и
и  . Таким образом,
. Таким образом,  и
и  - свободные неизвестные:
- свободные неизвестные: .
. ,
,  .
. ,
,  .
. ,
,  ,
,  ,
,  ).
). ,
,  .
. .
. .
. 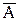 к специальному виду. При этом если в процессе преобразования появляются нулевые строки, то их отбрасывают.
к специальному виду. При этом если в процессе преобразования появляются нулевые строки, то их отбрасывают. (если
(если  , то можно начать с другого коэффициента, поменяв местами строки).
, то можно начать с другого коэффициента, поменяв местами строки). на
на  , получим матрицу вида
, получим матрицу вида  .
. ,
,  , …,
, …, 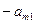 и прибавим полученные строки соответственно ко 2-й, 3-й, …, m-й строкам матрицы. В результате получим равносильную матрицу
и прибавим полученные строки соответственно ко 2-й, 3-й, …, m-й строкам матрицы. В результате получим равносильную матрицу ,
, и
и  - новые элементы матрицы.
- новые элементы матрицы. и произведя аналогичные преобразования (исключение неизвестного
и произведя аналогичные преобразования (исключение неизвестного  .
. . (6)
. (6) .
. .
. являются главными, а неизвестные
являются главными, а неизвестные  - свободными. В этом случае общее решение системы (5) имеет вид
- свободными. В этом случае общее решение системы (5) имеет вид .
. ~
~ ~
~  ~
~  Þ
Þ 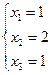 .
. ~
~  ~
~ Þ
Þ 
 Þ
Þ  ;
; Þ
Þ  .
. .
. ~
~  ~
~ 




