Задания для самостоятельной работы. 1.96.Определить энергию сферы радиуса R, равномерно заряженной зарядом q.
1.96. Определить энергию сферы радиуса R, равномерно заряженной зарядом q.
1.97. Сферическая оболочка, внутренний радиус которой R1, а внешний – R2, равномерно заряжена с объемной плотностью заряда r. Определить энергию электрического поля оболочки.
1.98. Три одинаковых точечных заряда q находятся в вершинах равностороннего треугольника со стороной а. Определить энергию взаимодействия системы.
1.99. Четыре точечных заряда расположены в вершинах квадрата со стороной а. Заряды, находящиеся на конце одной из диагоналей, одинаковы и равны q. Заряды в двух других вершинах также одинаковы и равны – q. Определить энергию взаимодействия системы.
1.100. Два одинаковых проводящих шара радиусами R заряжены зарядами q1 и q2 соответственно. Расстояние между центрами шаров l >> R. Определить полную энергию системы.
1.101. Точечный заряд q находится на расстоянии l от проводящей плоскости. Найти энергию взаимодействия заряда с плоскостью.
1.102. Две концентрические тонкие металлические оболочки радиусами R1 и R2 заряжены зарядами q1 и q2 соответственно. Определить собственные энергии оболочек и полную энергии системы.
1.103. Сферическую оболочку радиуса R1, равномерно заряженную зарядом q, расширили до радиуса R2. Найти работу, совершенную при этом электрическим полем.
1.104. В центре сферы радиуса R, равномерно заряженной по поверхности зарядом Q, находится точечный заряд q. Определить энергию взаимодействия заряда и сферы.
1.105. В центре сферической оболочки, равномерно заряженной по поверхности зарядом q, находится точечный заряд q0. Определить работу, совершаемую электрическим полем, при увеличении радиуса оболочки от R1 и R2. 1.106. Точечный заряд q находится в центре сферического проводящего незаряженного слоя с небольшим отверстием. Какую работу нужно совершить, чтобы переместить заряд из центра оболочки через отверстие в бесконечно удаленную точку. Внутренний радиус слоя равен a, внешний – b.
1.107. Плоский конденсатор, расстояние между обкладками которого равно d, в горизонтальном положении наполовину заполняют жидким диэлектриком с проницаемостью e. Затем конденсатор подключают к источнику напряжения U. Найти приращение давления жидкости в конденсаторе.
1.108. Неполярная молекула с поляризуемостью a находится на большом расстоянии l от полярной молекулы с дипольным моментом 1.109. Найти энергию взаимодействияэлектронного облака с ядром в атоме водорода. Заряд электрона распределен в атоме с объемной плотностью 1.110. Считая, что электронные облака обоих электронов в атоме гелия имеют одинаковый вид и характеризуются плотностью
1.111. Определить энергию сферического конденсатора, заряженного зарядом q. Радиусы обкладок R1 и R2 > R1.
1.112. Определить энергию, приходящуюся на единицу длины цилиндрического конденсатора, заряженного до напряжения U. Радиусы обкладок R1 и R2 > R1.
1.113. Точечный заряд q находится на расстоянии d от центра незаряженной проводящей заземленной сферы радиуса R < d. Определить энергию и силу взаимодействия заряда и сферы.
1.114. Сфера радиуса R заряжена с поверхностной плотностью заряда s = s0× cosj (j - широтный угол). Определить собственную энергию сферы.
ОТВЕТЫ
|

 . Определить силу взаимодействия молекул, если вектор
. Определить силу взаимодействия молекул, если вектор 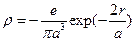 , где е – заряд электрона, а – боровский радиус атома.
, где е – заряд электрона, а – боровский радиус атома. , где е – заряд электрона и а – боровский радиус атома, определить энергию взаимодействия электронов.
, где е – заряд электрона и а – боровский радиус атома, определить энергию взаимодействия электронов.


