Примеры решения задач. Пример.Определить энергию магнитного поля, приходящуюся на единицу длины двухпроводной линии, по которой протекает ток J
Пример. Определить энергию магнитного поля, приходящуюся на единицу длины двухпроводной линии, по которой протекает ток J. Радиус первого проводника а, второго - b, расстояние между осями проводников d >> a, b, магнитная проницаемость материала проводников m. Найти индуктивность единицы длины линии. Индуктивность единицы длины линии может быть определена в соответствии с выражением (2.30) вычислением потока, пронизывающего плоскость контура единичной
Первый способ. Из рис. 2.7 видно, что полный поток Ф = Ф1 + Ф2 + Ф0, где Ф1 и Ф2 – потоки, пронизывающие сечения первого и второго проводников соответственно и Ф0 – поток, пронизывающий область между проводнимками. Используя результаты, полученные в примерах 2 п. 2.1.1 и 1 п. 2.2.1, индукцию магнитного поля в выделенных областях можно представить в виде:
Подчеркнем, что в выражениях для В 1 и В 2 r 1 и r 2 отсчитываются от осей соответствующих токов (для значения В 0 отсчет r не имеет значения). Т.к. векторы
Учитывая, что d >> a и b, получаем
Следовательно, Второй способ. Вычислим энергию магнитного поля единицы длины линии с помощью формулы (2.28), в которой
где А 1 = А 11 + А 21 и А 2 = А 22 + А 12, причем А 11 и А 22 - векторные потенциалы, создаваемые токами J и - J в области первого и второго проводников соответственно, А 21 – векторный потенциал, создаваемый током - J в области первого проводника, а А 12 – векторный потенциал, создаваемый током J в области второго проводника. Для указанных векторных потенциалов воспользуемся результатами, полученными в примере п. 2.2.1:
Здесь r 1 и r 2 отсчитываются от осей соответствующих токов, наличие постоянной С в выражениях для А 22 связано с тем, что потенциал отсчитывается от оси первого проводника. Тогда, полагая A 22 = 0 при r 2 = d, получаем
Учитывая, что a, b << d и поэтому пренебрегая изменением векторных потенциалов А 11 при r 1 > a и А 22 при r 2 > b в областях, занятых токами _ J и J соответственно, получаем:
Таким образом
Тогда энергия, приходящаяся на единицу длины линии, будет определяться как
Выполняя интегрирование, получаем
|

 длины, ограниченного осями токов (см. рис.2.7). При этом энергия, приходящаяся на единицу длины линии
длины, ограниченного осями токов (см. рис.2.7). При этом энергия, приходящаяся на единицу длины линии  (разумеется, L – индуктивность единицы длины линии). Возможен и другой способ расчета требуемых величин – непосредственное вычисление энергии единицы длины линии с последующим определением индуктивности.
(разумеется, L – индуктивность единицы длины линии). Возможен и другой способ расчета требуемых величин – непосредственное вычисление энергии единицы длины линии с последующим определением индуктивности. ,
,  ,
,  .
.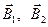 и
и  перпендикулярны плоскости, в которой лежат оси токов J 1 и J 2, то потоки, пронизывающие поверхность рассматриваемого контура единичной длины,
перпендикулярны плоскости, в которой лежат оси токов J 1 и J 2, то потоки, пронизывающие поверхность рассматриваемого контура единичной длины, ,
,  ,
,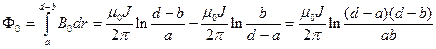 .
. и
и  . Тогда
. Тогда .
. и
и  .
.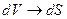 , т.е. выражение для энергии единицы длины линии принимает вид:
, т.е. выражение для энергии единицы длины линии принимает вид:
 ,
, , А 1 – векторный потенциал, создаваемый токами J и – J в области первого проводника, а А 2 – в области второго проводника. Здесь
, А 1 – векторный потенциал, создаваемый токами J и – J в области первого проводника, а А 2 – в области второго проводника. Здесь при r 1 £ a и
при r 1 £ a и  при r 1 ³ a;
при r 1 ³ a; при r 2 £ b и
при r 2 £ b и  при r 2 ³ b.
при r 2 ³ b.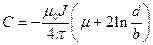 и
и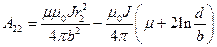 при r 2 £ b,
при r 2 £ b,  при r 2 ³ b.
при r 2 ³ b. и
и  .
. и
и  .
.



