Гипотезы прочности
Гипотезы прочности Всякий расчет на прочность предваряется определением напряженно-деформированного состояния. Для этого используют аналитические, вычислительные и экспериментальные методы. После определения НДС нередко возникает вопрос о дальнейших действиях. Традиционно отыскивают опасную точку, и нарушение прочности в этой одной точке связывают с тем, что при этом и вся конструкция достигает предельного состояния. Вообще говоря, это не всегда так, а во многих случаях совсем не так. Но, оставаясь в рамках традиции, опасной точкой называют такую, в которой эквивалентное напряжение, выбранное по той или иной гипотезе (теории) прочности[1], максимально. Цель расчета на прочность найти коэффициент запаса прочности и сопоставить его с допускаемым запасом
равен запасу для данного, не одноосного напряженного состояния. Равенство запасов прочности означает, что эти разные (не одноосное, полученное в точке, и эквивалентное) напряженные состояния равнопрочны в определенном смысле и этот смысл устанавливается гипотезами прочности. Условие равнопрочности разных (неподобных[2]) напряженных состояний составляет предмет гипотез прочности и позволяет эквивалентное напряжение выразить через главные напряжения данного, не одноосного, напряженного состояния и тогда На настоящее время существует около сотни гипотез прочности. Это признак сложности явления и недостаточной его изученности. Практическое применение имеют всего несколько гипотез. Первые пять гипотез так, по номерам, и именуются. Первая гипотеза прочности предложена Галилеем и формулируется следующим образом: два неподобных напряженных состояний равнопрочны, если у них равны наибольшие нормальные напряжения. Отсюда вытекает, что
Эта гипотеза хорошо описывает хрупкое разрушение, путем отрыва, и применяется до сих пор. Вторая гипотеза предложена Мариоттом и утверждает, что критерием равнопрочности служит наибольшая линейная деформация. Отсюда эквивалентное напряжение равно
Эта гипотеза, как и первая, описывает хрупкое разрушение. Полученные выражения для эквивалентных напряжений изобразим графически для плоского напряженного состояния. На рис. 1.4 показаны области допустимых состояний по первой и второй гипотезам прочности в плоскости двух главных напряжений. Линии
Рис. 1.4. Области допустимых состояний по I – ой (квадраты) и II – ой (ромбы) теориям прочности.
Третья гипотеза прочности предложена Кулоном и Треска и утверждает, что критерием равнопрочности служит наибольшее касательное напряжение. Отсюда следует
Эта гипотеза описывает наступление пластического течения или же разрушение путем среза. Четвертая гипотеза прочности предложена Губером и Мизесом и утверждает, что неподобные напряженные состояния равнопрочны, если у них равны удельные энергии изменения формы в точке. Отсюда получаем Эта гипотеза, как и третья, описывает наступление пластического течения или разрушения путем среза. Области допустимых состояний графически показаны на рис. 1.5.
Рис. 1.5. Области допустимых состояний по III – ей (шестиугольник) и IV – ой (эллипс) теориям прочности
Далее рассмотрим гипотезу прочности, предложенную Мором (можно назвать её пятой), которая утверждает, что разрушение наступает, когда круг напряжений данного напряженного состояния (круг Мора) коснется предельной огибающей. Эта огибающая представляет собой механическую характеристику материала и должна находиться из опыта. Промежуточное главное напряжение
Здесь Графическое отображение теории Мора показано на рис. 1.6. Диаметр круга Мора при одноосном растяжении (отмечен на рис. как 1) дает напряжение растяжения. Если это напряжение увеличить, диаметр возрастет и когда круг (отмечен как 2) коснется предельной огибающей, наступит разрушение. Это разрушение произойдет по площадке, нормаль к которой проходит через точку касания. На площадке разрушения действуют и нормальные Форма предельной кривой такова, что при всестороннем растяжении При достаточно больших сжимающих напряжений (
Рис. 1.6. Предельная огибающая Мора (линия параболического типа)
Эту гипотезу трактуют и по другому. Разумно предположить, что предельное касательное напряжение зависит от нормального на этой же площадке. Тогда разрушение произойдет, когда касательное напряжение достигнет предельного, т.е.
Слева, по определению, эквивалентное касательное напряжение для эквивалентного напряженного состояния в виде чистого сдвига. В этом варианте, как и в первом, Указания на то, какой вид разрушения описывает гипотеза прочности, помогает выбору гипотезы для расчета коэффициентов запаса. В качестве полезного примера использования гипотез прочности найдем связь между пределами текучести при растяжении и чистом сдвиге. При наступлении пластического течения при растяжении напряжение равно пределу текучести По четвертой (энергетической) гипотезе прочности Находит применение гипотеза прочности Г.С. Писаренко и А.А. Лебедева, записываемая следующим образом
При k = 0 эта гипотеза совпадает с первой, при k = 1 с четвертой (
Суммируя изложенное ясно, что предельное состояние любого напряженного состояния достигается при выполнении критериального условия вида Эти гипотезы определяют наступление предельного состояние в точке[3], т.е. в локальной области тела. Дальнейшее развитие (распространение) области предельного состояния материала по объему тела нуждается в специальном изучении. Достижение предельного состояния в одной точке не обязано совпадать с достижением предельного состояния всего тела (потери его несущей способности). Гипотезы, описывающие хрупкое разрушение (первая, вторая) по сути, описывают зарождение трещины. Дальнейший её рост определяется положениями механики разрушения. В силу опасности хрупкого разрушения можно отождествлять наступление предельного состояния в точке с предельным состоянием всего тела. Гипотезы, описывающие появление пластического течения в опасной точке (при этом эквивалентное напряжение, по третьей или четвертой гипотезе, равно пределу текучести) только это и констатируют. Дальнейшее распространение пластической области (зоны) по телу приводит к уменьшению жесткости и несущей способности тела. Предельное состояние всего тела будет достигнуто при достаточно больших размерах пластических зон (типа шейки или пластического шарнира[4]). Эти гипотезы описывают также и разрушение путем среза, когда эквивалентное напряжение достигает предела прочности при растяжении (в этом случае приближенно полагается, что формулы теории упругости годны и на момент разрушения). Обратим внимание на эффекты, связанные с разной прочностью при растяжении и сжатии. Рис. 1.4 показывает, что увеличение пределов прочности на сжатие
[2] Напряженные состояния подобны, если соблюдается условие [3] Это опасная точка, т.е. та точка, в которой эквивалентное напряжение достигает максимума среди всех прочих точек тела. [4] В переводной литературе этот вариант потери несущей способности носит название «пластической нестабильности» или «пластического коллапса».
|


 , который принят в данной области техники, т.е. должно быть
, который принят в данной области техники, т.е. должно быть  . Механические свойства, оценивающие прочность материала находят при одноосном напряженном состоянии (при растяжении – это предел текучести
. Механические свойства, оценивающие прочность материала находят при одноосном напряженном состоянии (при растяжении – это предел текучести  или предел прочности
или предел прочности  ). Поэтому предельное напряжение (
). Поэтому предельное напряжение ( либо
либо  ). Становится неясным, на что же делить предельное напряжение в таком случае для получения запаса прочности. Для разрешения возникшей проблемы мысленно вводят одноосное напряженное состояние, называемое эквивалентным. В нем действует эквивалентное напряжение. Если эквивалентное напряжение известно, то для него можно подсчитать запас прочности (поскольку оно одноосное). Термин эквивалентное означает, что запас прочности, подсчитанный для эквивалентного напряженного состояния
). Становится неясным, на что же делить предельное напряжение в таком случае для получения запаса прочности. Для разрешения возникшей проблемы мысленно вводят одноосное напряженное состояние, называемое эквивалентным. В нем действует эквивалентное напряжение. Если эквивалентное напряжение известно, то для него можно подсчитать запас прочности (поскольку оно одноосное). Термин эквивалентное означает, что запас прочности, подсчитанный для эквивалентного напряженного состояния
 .
. .
. .
. , ограничивающие эти области, это линии постоянного предельного эквивалентного напряжения.
, ограничивающие эти области, это линии постоянного предельного эквивалентного напряжения.
 .
. .
.
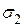 не принимается во внимание. Теория предельных состояний Мора допускает различие сопротивлений материала сжатию и растяжению. Для ограниченной области напряженных состояний (при
не принимается во внимание. Теория предельных состояний Мора допускает различие сопротивлений материала сжатию и растяжению. Для ограниченной области напряженных состояний (при  не больше предельного при растяжении и
не больше предельного при растяжении и  не меньше предельного при сжатии)
не меньше предельного при сжатии) .
.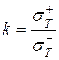 или
или  . Индексы «плюс» и «минус» означают растяжение и сжатие.
. Индексы «плюс» и «минус» означают растяжение и сжатие. и касательные
и касательные  напряжения. Отсюда следует, что эта гипотеза прочности отражает смешанное разрушение (по тем площадкам, по которым действует некая комбинация нормальных и касательных напряжений).
напряжения. Отсюда следует, что эта гипотеза прочности отражает смешанное разрушение (по тем площадкам, по которым действует некая комбинация нормальных и касательных напряжений). (здесь круги Мора превращаются в точку на правом конце предельной огибающей) гипотеза Мора совпадает с первой теорией (самая правая точка на оси абсцисс). Причем точка пересечения предельной кривой с осью абсцисс не выявляется одноосным напряженным состоянием, поскольку соответствующий круг напряжений (обозначенный цифрой 2) не пролезает в узкую часть допустимой области. В эту узкую часть можно влезть, создав растяжение по двум другим главным направлениям (напряженное состояние с тремя кругами). Правая точка предельной кривой отражает сопротивление отрыву при равномерном всестороннем растяжении напряжениями р.
(здесь круги Мора превращаются в точку на правом конце предельной огибающей) гипотеза Мора совпадает с первой теорией (самая правая точка на оси абсцисс). Причем точка пересечения предельной кривой с осью абсцисс не выявляется одноосным напряженным состоянием, поскольку соответствующий круг напряжений (обозначенный цифрой 2) не пролезает в узкую часть допустимой области. В эту узкую часть можно влезть, создав растяжение по двум другим главным направлениям (напряженное состояние с тремя кругами). Правая точка предельной кривой отражает сопротивление отрыву при равномерном всестороннем растяжении напряжениями р. ) теория Мора начинает совпадать с третьей. Одновременно видно, что сопротивление материала всестороннему сжатию (в отличие от всестороннего растяжения) практически не ограничена.
) теория Мора начинает совпадать с третьей. Одновременно видно, что сопротивление материала всестороннему сжатию (в отличие от всестороннего растяжения) практически не ограничена.
 . Здесь
. Здесь  разрушающие напряжения на той площадке, вдоль которой произойдет разрушение,
разрушающие напряжения на той площадке, вдоль которой произойдет разрушение, 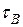 предел прочности при чистом сдвиге, а число
предел прочности при чистом сдвиге, а число  играет роль коэффициента трения (внутреннего). Видно, что сжимающие нормальные напряжения приводят к увеличению сопротивления разрушению, а растягивающие, наоборот, способствуют разрушению. Угол
играет роль коэффициента трения (внутреннего). Видно, что сжимающие нормальные напряжения приводят к увеличению сопротивления разрушению, а растягивающие, наоборот, способствуют разрушению. Угол  между направлением первого главного напряжения и нормалью к площадке разрушения находится из соотношения
между направлением первого главного напряжения и нормалью к площадке разрушения находится из соотношения  . Критериальное соотношение можно переписать через главные напряжения (плоское напряженное состояние)
. Критериальное соотношение можно переписать через главные напряжения (плоское напряженное состояние) .
. не должны сильно удаляться от
не должны сильно удаляться от  .
. , оно же есть и эквивалентное напряжение по определению. При чистом сдвиге
, оно же есть и эквивалентное напряжение по определению. При чистом сдвиге  ,
, 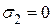 . По третьей гипотезе прочности эквивалентное напряжение равно
. По третьей гипотезе прочности эквивалентное напряжение равно  . При наступлении текучести
. При наступлении текучести  . Эквивалентные напряжения должны быть равны, следовательно,
. Эквивалентные напряжения должны быть равны, следовательно,  или предел текучести при сдвиге
или предел текучести при сдвиге  .
. . Это эквивалентное напряжение равно напряжению в эквивалентном состоянии, а оно равно пределу текучести
. Это эквивалентное напряжение равно напряжению в эквивалентном состоянии, а оно равно пределу текучести  или
или  . Эксперимент в этой задаче лучше соответствует четвертой гипотезе прочности.
. Эксперимент в этой задаче лучше соответствует четвертой гипотезе прочности. .
. - интенсивность напряжений). Укажем также на критерий В.П. Сдобырева, объединяющий критерии хрупкого и вязкого разрушения, эквивалентное напряжение для которого имеет вид
- интенсивность напряжений). Укажем также на критерий В.П. Сдобырева, объединяющий критерии хрупкого и вязкого разрушения, эквивалентное напряжение для которого имеет вид .
. , где ni – постоянные материала, определяемые экспериментально. При этом добавим, что функцию F следует выбирать исходя из физических соображений, а не абстрактных математических.
, где ni – постоянные материала, определяемые экспериментально. При этом добавим, что функцию F следует выбирать исходя из физических соображений, а не абстрактных математических. приводит к увеличению области допустимых сжимающих напряжений. Видно также, что области с напряжениями разных знаков более опасны, чем области с напряжениями одинаковых знаков. Эта же тенденция отмечается и согласно третьей и четвертой теорий прочности (рис. 1.5). Наибольшее расхождение между точками эллипса и шестигранника (в первом и третьем квадрантах) составляет 16%. В этих теориях пределы прочности на растяжение и сжатие принимаются одинаковыми.
приводит к увеличению области допустимых сжимающих напряжений. Видно также, что области с напряжениями разных знаков более опасны, чем области с напряжениями одинаковых знаков. Эта же тенденция отмечается и согласно третьей и четвертой теорий прочности (рис. 1.5). Наибольшее расхождение между точками эллипса и шестигранника (в первом и третьем квадрантах) составляет 16%. В этих теориях пределы прочности на растяжение и сжатие принимаются одинаковыми. . Если штрихованное напряженное состояние предельное, то эти дроби равны запасу прочности данного напряженного состояния.
. Если штрихованное напряженное состояние предельное, то эти дроби равны запасу прочности данного напряженного состояния.


