Механические состояния материала
Механические состояния материала Привычное представление о механическом поведении материала дает диаграмма деформирования (связь напряжения с соответствующей деформацией), которая получается экспериментально при одноосном напряженном состоянии. При сложном (двухосном, трехосном) напряженном состоянии диаграмма деформирования настолько сильно может отличаться от диаграммы одноосного растяжения, что возникает впечатление другого материала. Проиллюстрируем это на трехосном (объемном) напряженном состоянии вида: растяжение
Рис. 1.7. Пример объемного напряженного состояния
Рассмотрим деформацию по первому главному направлению для данного сложного напряженного состояния При k = 0 – одноосное растяжение, при k = В этом примере важно обратить внимание, что обсуждаемый эффект вызван непропорциональным нагружением (коэффициент k не зависит от напряжения
Рис. 1.8. Диаграммы деформирования при трехосном напряженном состоянии (показанном на рис 1.7) в направлении первого главного напряжения
Известны опыты Кармана с мрамором, который в обычном состоянии хрупкий. Но если приложить к образцу боковое давление и создать тем самым отрицательное среднее напряжение (рис. 1.9), то мрамор становится пластичным (круги Мора уходят далеко налево, максимальные касательные напряжения достигают предела текучести, а растягивающих напряжений попросту нет).
Рис. 1.9. Нагружение цилиндрического образца при всестороннем сжатии
Соответствующие экспериментальные диаграммы деформирования показаны на рис. 1.10. Диаграммы деформирования построены в координатах: по ординатам удвоенное максимальное касательное напряжение, а по абсциссе деформация в осевом направлении. Диаграмма при одноосном сжатии (
Рис. 1.10. Диаграммы деформирования мрамора в опытах Кармана. Числа у кривых – третье главное напряжение (боковое)
Эффект скорости нагружения схематически отражен на диаграмме Людвига (1929). На схеме представлено несколько диаграмм растяжения для разных скоростей нагружения (рис. 1.11). Эти диаграммы сверху ограничивает сопротивление отрыву, слабо зависящее от скорости нагружения. При больших скоростях нагружения диаграммы крутые, пластичность мала, разрушение хрупкое. При малых скоростях диаграммы пологие, предел текучести мал, пластичность велика. В дальнейшем Н.Н. Давиденков ввел сопротивление вязкому отрыву, которое на его схеме ограничивает диаграммы справа (линия 1 на рис. 1.12).
Рис. 1.11. Диаграмма механического состояния Людвика
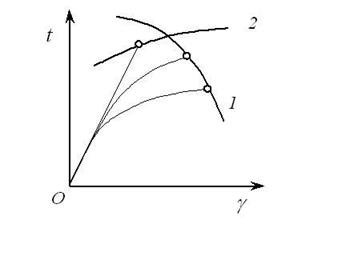
Схема Н.Н. Давиденкова (1936) поясняет влияние напряженного состояния на вид разрушения. Диаграммы разрушения (разные при разных напряженных состояниях) заканчиваются на линиях вязкого (1) и хрупкого (2) отрыва (рис. 1.12). Положение этих линий (которые отражают свойства материала) может смещаться в зависимости от условий нагружения. По ординатам отложены истинные наибольшие касательные напряжения
Рис. 1.12. Диаграмма механического состояния Давиденкова
А.И. Иоффе (1924) схематически объяснил наличие критической температуры хрупкости (порог хладноломкости). Сопротивление отрыву (ориентировочно равно истинному сопротивлению разрыву
Рис. 1.13. Схема Иоффе, поясняющая критическую температуру хрупкости
Критическая температура хрупкости смещается в сторону более высоких температур (приводя к расширению температурной области хрупких разрушений) при уменьшении радиусов кривизны в зонах концентрации напряжений, при увеличении размеров тела, при увеличении скорости нагружения. Переход от вязкого разрушения к хрупкому не всегда резок, как это следует из схемы Иоффе. Практически всегда переходная область размыта как это видно из обычной картины экспериментальных точек (рис. 1.14).
Рис. 1.14. Зависимость ударной вязкости образцов Шарпи (KCV) от температуры[2]
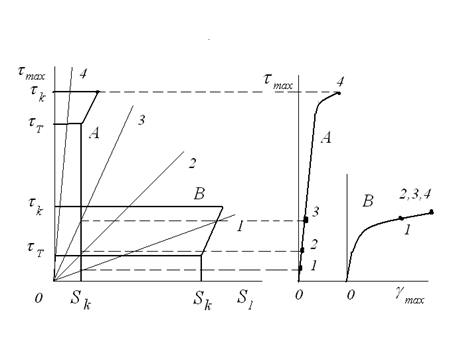
Размытость переходной области привела к появлению разных формулировок моментов хрупко-вязкого перехода. В наше время существуют несколько критериев для определения критической температуры хрупкости. Каждому критерию соответствует своя критическая температура. Поэтому выбор критерия основан на тенденциях данной области техники. В основном критерии основаны на сериальных испытаниях образцов на ударную вязкость, которые показывают заметное снижение этой характеристики с уменьшением температуры испытания. Критическую температуру выбирают при некотором характерном значении ударной вязкости. Заметим, что критическая температура не зависит от действующего в конструкции напряжения. Ударная вязкость не входит в расчетные уравнения, но она отражает любые нарушения технологии при производстве металла, и поэтому испытания на ударную вязкость необходимый этап на заводе-изготовителе при сдаче металла заказчику. В частности, увеличение диаметра зерна с мелкозернистого уровня на крупнозернистый приводит к существенному уменьшению ударной вязкости, при том, что обычные статические характеристики сохраняются практически неизменными. Проиллюстрируем охрупчивание материала в виде повышения критической температуры в процессе эксплуатации некоторой конструкции на конкретном примере. Критическая температура хрупкости стали 09Г2С листа для коксовой камеры в исходном состоянии равна минус 65 º С. После длительной эксплуатации при температуре стенки камеры 450 º С критическая температура хрупкости стали повысилась до плюс 2 º С (определенной тем же методом). К этому привело длительное термическое воздействие среды на материал камеры в процессе её эксплуатации. В энергетике принято определять две критические температуры хрупкости - первую Приведенные схемы показывают, что один и тот же материал в зависимости от вида напряженного состояния, скорости нагружения или температуры при разрушении может находиться как в хрупком (упругом), так и в вязком (пластическом) состоянии. Рассмотрим деталь в виде заклепки. Она соединяет (прижимает) два листа, препятствуя скольжению одного листа по другому. В сечении заклепки на уровне стыка листов возникает деформация сдвига, которая заканчивается разрушением путем среза. Это разрушение происходит от максимальных касательных напряжений, достигающих сопротивления материала срезу Наглядное представление о механическом состоянии материала можно получить из диаграммы механического состояния Я.Б. Фридмана (1941). Она состоит из двух графиков (рис. 1.15). Левый график строят в координатах
Рис. 1.15. Диаграмма механического состояния Фридмана
Линия напряженного состояния на левом графике может пересечь линию отрыва, тогда будет хрупкое разрушение отрывом (например, при растяжении) и точка их пересечения (точка 1) на правом графике покажет конец диаграммы деформации (практически линейной). Если линия напряженного состояния пересекает линию вязкого отрыва (линия 2), то эта точка пересечения укажет (на правом графике точка 2) конец диаграммы деформирования. Диаграмма изогнута перед точкой вязкого отрыва, что свидетельствует о наличии пластической деформации перед разрушением. Наконец, если линия (3) напряженного состояния пересекает уровень предела текучести и затем достигает сопротивления срезу, то диаграмма деформирования будет самой длинной, пластичность максимальна, разрушение произойдет путем среза (точка 3 справа). Видно, что разрушение, как ножницами, отрезает обобщенную диаграмму деформации. Поэтому прочность образца (ординаты конечной точки диаграммы деформации) и его пластичность (абсцисса конечной точки диаграммы) оказываются зависящими от напряженного состояния, равно как и вид разрушения (хрупкий отрыв, вязкий отрыв, срез). Разные материалы имеют разное соотношение между сопротивлениями отрыву и срезу. Соответственно меняется и вид диаграммы механического состояния. На рис. 1.16 показаны диаграммы для двух разных материалов А и В. Линии 1,2,3,4 из начала координат на левом графике соответствуют растяжению, кручению, сжатию и вдавливанию. В зависимости от того, где эти линии пересекают сопротивление отрыву, срезу и начала течения на правом графике диаграммы соответствующие точки (на том же конечном уровне напряжений) отрезают диаграмму деформирования.
Рис. 1.16. Диаграммы механического состояния Я.Б. Фридмана для двух разных материалов. Точки на правом графике – концы диаграмм деформирования для соответствующих видов нагружения 1,2,3,4
Материал А более хрупок, материал В более пластичен. Для материала А пластическое течение появляется только в условиях преобладающих касательных напряжений при вдавливания, а при растяжение, кручении и обычном сжатии разрушение хрупкое с разными разрушающими напряжениями. В материале В диаграмма деформирования практически не меняется при кручении, сжатии и вдавливании и только немного уменьшается пластичность при растяжении, Отметим немаловажную роль масштабного фактора, который указывает на падение прочности с увеличением абсолютных размеров образца. Ориентировочное соотношение таково: Все здесь изложенное указывает, что в реальной конструкции детали могут вести себя совершенно не так, как демонстрируют стандартные испытания на растяжение. Очевидно также, что при проектировании и при постановке экспериментов следует учитывать различие механического поведения конструкции и стандартного образца, которое тем больше, чем больше разница между их диаграммами деформирования (естественно, с сохранением идентичности параметров на координатных осях). Диаграмма В обобщенной диаграмме деформирования напряжения и деформации должны быть истинными, которые находят, обрабатывая обычную диаграмму растяжения. Удачным обстоятельством оказывается то, что истинное напряжение обычной диаграммы растяжения Можно поступить немного по другому. Вычислить абсциссу точки Можно также аппроксимировать обобщенную диаграмму истинных напряжений (только до предела прочности) степенной зависимостью вида
Здесь Приближенные методы аппроксимации обобщенной диаграммы вполне достаточны для практических целей, в частности, для введения её в качестве исходных данных при расчетах прочности в коммерческих программах. Несущая способность детали может быть исчерпана при достижении деформацией предельного значения, которое зависит от вида напряженного состояния. Это видно, например, на правой части диаграммы Фридмана, на которой разрушение отрезает обобщенную диаграмму деформации при данном виде напряженного состояния. Поэтому следует вести расчет не только по напряжениям, но и по предельной деформации, определяемой экспериментально. Это требует специального эксперимента на образцах и установках, способных создавать разные виды напряженного состояния. Сказанное можно проиллюстрировать на результатах опыта с построением обобщенных диаграмм при разных напряженных состояниях в координатах «октаэдрическое касательное напряжение – логарифмический октаэдрический сдвиг» (рис. 1.17). Испытанию подвергались стальные трубки при пропорциональном нагружении с разным сочетанием внутреннего давления и осевой растягивающей силы. Одинаковые точки соответствуют данному напряженному состоянию. Видно хорошее соответствие экспериментальных точек с обобщенной кривой (кривая одна, но на рисунке сдвинута для случаев разрыва поперек и вдоль трубы). Разрушение на диаграммах отмечено символом R. Каждому виду напряженного состояния отвечает свой момент разрушения (число точек R равно числу разных напряженных состояний в этом эксперименте) и, следовательно, своя разрушающая (предельная) деформация.
Рис. 1.17. Обобщенная диаграмма с экспериментальными точками и отметкой момента разрушения
Можно использовать обычные испытательные машины на растяжение. С этой целью следует изготовить серию образцов с надрезами разной формы, в которых можно воспроизвести разные напряженные состояния[4]. Рассчитать (численно) напряженно-деформированное состояние в области надреза и соотнести полученную максимальную деформацию с внешней силой. Рассчитать в точке максимальной деформации параметр Лодэ, количественно отражающий вид напряженного состояния
[2] Обозначения ударной вязкости по ГОСТ 9454-78 – образцы Менаже KCU, Шарпи KCV, Дроздовского KCT. Последняя буква в обозначении указывает форму надреза (Т – трещина). [3] Более независима от вида напряженного состояния диаграмма в координатах «истинное октаэдрическое касательное напряжение – истинный октаэдрический сдвиг». [4] Подобный эксперимент описан в работе: Захаров М.Н. Известия ВУЗов. Нефть и газ. 2000. № 3.
|

 , два других главных напряжения одинаковы и равны
, два других главных напряжения одинаковы и равны  (рис. 1.7).
(рис. 1.7).
 . Введем одноосное эквивалентное напряженное состояние
. Введем одноосное эквивалентное напряженное состояние 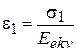 . Эквивалентность состоит в том, что в разных напряженных состояниях деформации
. Эквивалентность состоит в том, что в разных напряженных состояниях деформации 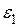 и напряжения
и напряжения 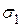 равны. Эквивалентный модуль упругости равен
равны. Эквивалентный модуль упругости равен 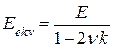 . Следовательно, наклон линии упругого нагружения зависит от напряженного состояния. В пластической области в эквивалентном напряженном состоянии имеем ту же пластическую деформацию (в направлении
. Следовательно, наклон линии упругого нагружения зависит от напряженного состояния. В пластической области в эквивалентном напряженном состоянии имеем ту же пластическую деформацию (в направлении 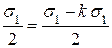 или
или  .
.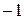 модуль меньше и диаграмма ниже в два раза, при
модуль меньше и диаграмма ниже в два раза, при 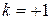 пластических деформаций вообще не возникает. Вид разрушения также меняется. Отрицательные коэффициенты k приводят к вязкому разрушению, положительные к хрупкому (рис. 1.8).
пластических деформаций вообще не возникает. Вид разрушения также меняется. Отрицательные коэффициенты k приводят к вязкому разрушению, положительные к хрупкому (рис. 1.8).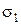 ).
).

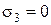 ) совсем маленькая и практически прямая. С увеличением бокового давления возрастает прочность и, что важно, пластичность. Таким способом Карману удалось отштамповать мраморную медаль с барельефом австро-венгерского императора Франца-Иосифа к его юбилею.
) совсем маленькая и практически прямая. С увеличением бокового давления возрастает прочность и, что важно, пластичность. Таким способом Карману удалось отштамповать мраморную медаль с барельефом австро-венгерского императора Франца-Иосифа к его юбилею.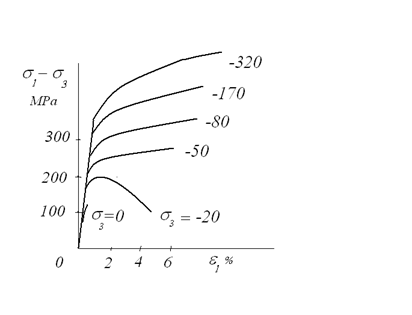
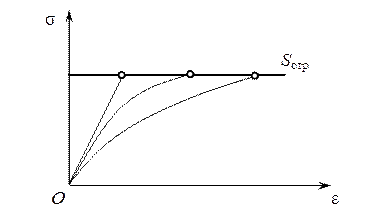
 , вдоль абсцисс истинный сдвиг
, вдоль абсцисс истинный сдвиг  . Здесь обозначено: S истинные напряжения, e истинные (логарифмические) деформации[1],
. Здесь обозначено: S истинные напряжения, e истинные (логарифмические) деформации[1],  .
.
 ) практически постоянно с ростом температуры, в то время, как предел текучести
) практически постоянно с ростом температуры, в то время, как предел текучести  падает (рис. 1.13). Температура точки пересечения этих двух зависимостей называется критической, поскольку она разделяет температурную область вязкого разрушения от хрупкого. Справа область вязкого разрушения, поскольку с ростом напряжения (при фиксированной температуре) сначала происходит пластическое течение, а потом разрушение. Слева область хрупкого разрушения, поскольку напряжение достигает сопротивления отрыва, не достигнув начала пластического течения.
падает (рис. 1.13). Температура точки пересечения этих двух зависимостей называется критической, поскольку она разделяет температурную область вязкого разрушения от хрупкого. Справа область вязкого разрушения, поскольку с ростом напряжения (при фиксированной температуре) сначала происходит пластическое течение, а потом разрушение. Слева область хрупкого разрушения, поскольку напряжение достигает сопротивления отрыва, не достигнув начала пластического течения.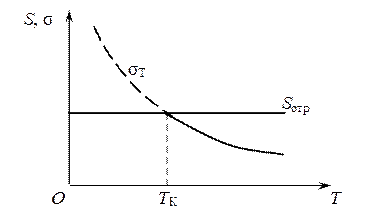

 и вторую
и вторую 
 . При
. При 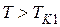 разрушение вязкое, при
разрушение вязкое, при  имеем область температур квазихрупкого разрушения, иначе, переходного состояния материала (разрушающее напряжение образца с трещиной выше предела текучести, но ниже предела прочности), при
имеем область температур квазихрупкого разрушения, иначе, переходного состояния материала (разрушающее напряжение образца с трещиной выше предела текучести, но ниже предела прочности), при  разрушение хрупкое. Температуру
разрушение хрупкое. Температуру  . Если заклепку растягивать вдоль её оси, то при достаточно низкой температуре произойдет хрупкое разрушение, без образования шейки, путем отрыва, от максимальных растягивающих напряжений
. Если заклепку растягивать вдоль её оси, то при достаточно низкой температуре произойдет хрупкое разрушение, без образования шейки, путем отрыва, от максимальных растягивающих напряжений  . Если растягивать заклепку при достаточно высокой температуре, то произойдет вязкое (пластическое) разрушение с образованием шейки. При этом напряжение равно истинному сопротивлению разрыву
. Если растягивать заклепку при достаточно высокой температуре, то произойдет вязкое (пластическое) разрушение с образованием шейки. При этом напряжение равно истинному сопротивлению разрыву 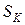 , а истинная пластическая деформация при разрыве
, а истинная пластическая деформация при разрыве  найдется из условия постоянства объема в пределах шейки
найдется из условия постоянства объема в пределах шейки 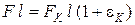 , или
, или 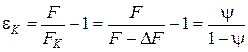 . Полная деформация равна сумме
. Полная деформация равна сумме  . Сопротивление материала срезу
. Сопротивление материала срезу 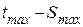 , правый в
, правый в  . На левом, вид напряженного состояния отражен тангенсом угла наклона луча из начала координат
. На левом, вид напряженного состояния отражен тангенсом угла наклона луча из начала координат  . Этот тангенс в частности равен 0,5 при растяжении (линия 1), единице при кручении (линия 2), больше единицы при сжатии (линия 3). Сразу заметим, что для простоты на оси ординат истинное касательное напряжение t можно заменить обычным
. Этот тангенс в частности равен 0,5 при растяжении (линия 1), единице при кручении (линия 2), больше единицы при сжатии (линия 3). Сразу заметим, что для простоты на оси ординат истинное касательное напряжение t можно заменить обычным  , а на оси абсцисс истинное напряжение
, а на оси абсцисс истинное напряжение  величиной
величиной 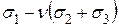 согласно второй. Область упругих состояний ограничена справа сопротивлением материала отрыву
согласно второй. Область упругих состояний ограничена справа сопротивлением материала отрыву  , сверху пределом текучести
, сверху пределом текучести  . Область пластических состояний справа ограничена сопротивлением вязкому отрыву, а сверху сопротивлением срезу
. Область пластических состояний справа ограничена сопротивлением вязкому отрыву, а сверху сопротивлением срезу  . Правый график представляет собой обобщенную диаграмму деформирования «
. Правый график представляет собой обобщенную диаграмму деформирования «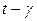 » (одинаковую для любых напряженных состояний при пропорциональном нагружении).
» (одинаковую для любых напряженных состояний при пропорциональном нагружении).
 где эмпирический показатель
где эмпирический показатель  . Здесь
. Здесь 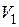 ; прочность
; прочность  большего объема
большего объема 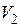 будет меньше, согласно приведенной зависимости.
будет меньше, согласно приведенной зависимости. в правой части диаграммы механического состояния Я.Б.Фридмана, как и диаграмма в координатах «интенсивность напряжений
в правой части диаграммы механического состояния Я.Б.Фридмана, как и диаграмма в координатах «интенсивность напряжений 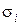 - интенсивность деформаций
- интенсивность деформаций 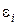 », как иногда считается[3], не зависит от вида напряженного состояния (поэтому её называют обобщённой), поскольку каждая из величин на соответствующих координатных осях пропорциональна одна другой.
», как иногда считается[3], не зависит от вида напряженного состояния (поэтому её называют обобщённой), поскольку каждая из величин на соответствующих координатных осях пропорциональна одна другой. равно интенсивности напряжений
равно интенсивности напряжений  , истинный предел прочности
, истинный предел прочности  , тангенс угла наклона касательной к истинной диаграмме в точке
, тангенс угла наклона касательной к истинной диаграмме в точке  равен
равен  . Начиная с этой точки, диаграмма практически прямая вплоть до напряжения
. Начиная с этой точки, диаграмма практически прямая вплоть до напряжения  (полученной из условия несжимаемости элементов объема в шейке). Далее из этой точки провести касательную к обычной диаграмме растяжения (В.И. Феодосьев). При этом обобщенная диаграмма состоит из начального участка обычной диаграммы (в условных координатах) и её продолжения в виде касательной до точки с координатами (
(полученной из условия несжимаемости элементов объема в шейке). Далее из этой точки провести касательную к обычной диаграмме растяжения (В.И. Феодосьев). При этом обобщенная диаграмма состоит из начального участка обычной диаграммы (в условных координатах) и её продолжения в виде касательной до точки с координатами ( ).
). при
при  и
и 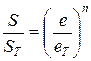 при
при  .
. ,
,  - показатель упрочнения (примерно равен истинной деформации на пределе прочности
- показатель упрочнения (примерно равен истинной деформации на пределе прочности 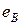 ),
),  ,
,  - расчетный предел текучести,
- расчетный предел текучести,  . Это выражение получено как ордината точки пересечения линейной и параболической частей диаграммы.
. Это выражение получено как ордината точки пересечения линейной и параболической частей диаграммы.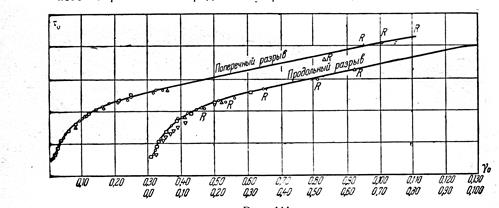
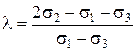 . Далее провести эксперимент до разрушения образцов, с замером разрушающей силы. По этой силе найти деформацию на момент разрыва (предельная пластичность), причем параметр Лодэ для этого образца известен. Таким образом, можно построить график зависимости предельной пластичности от параметра Лодэ. Это позволит наряду с расчетом по предельному напряжению (в качестве которого может выступать истинное сопротивление разрыву) можно вести расчет и по предельной пластичности в опасной точке детали..
. Далее провести эксперимент до разрушения образцов, с замером разрушающей силы. По этой силе найти деформацию на момент разрыва (предельная пластичность), причем параметр Лодэ для этого образца известен. Таким образом, можно построить график зависимости предельной пластичности от параметра Лодэ. Это позволит наряду с расчетом по предельному напряжению (в качестве которого может выступать истинное сопротивление разрыву) можно вести расчет и по предельной пластичности в опасной точке детали..
 , откуда
, откуда  , поскольку по определению сужение
, поскольку по определению сужение  .
. 


