Задача №4-5.
Решить задачу линейного программирования двумя способами (графическим и симплекс-методом). Для изготовления двух видов продукции используется три вида сырья. При производстве единицы продукции первого вида затрачивается А1 кг сырья первого вида, А2 кг сырья второго вида и А3 кг сырья третьего вида. При производстве единицы продукции второго вида затрачивается Б1 кг сырья первого вида, Б2 кг сырья второго вида и Б3 кг сырья третьего вида. Запасы сырья первого вида составляют Запасы1 кг, второго – Запасы2 кг, третьего – Запасы3 кг. Прибыль от реализации единицы продукции первого вида составляет С1 ден. ед., прибыль от реализации единицы продукции второго вида составляет С2 ден. ед. Определить оптимальный план выпуска продукции(количество выпускаемой продукции округлить до целого числа), чтобы прибыль от реализации была максимальной.
А1=9, А2=6, А3=5, В1=3, В2=12, В3=8, Запасы1=230, Запасы2=210, Запасы3=250, C1=18, C2=20.
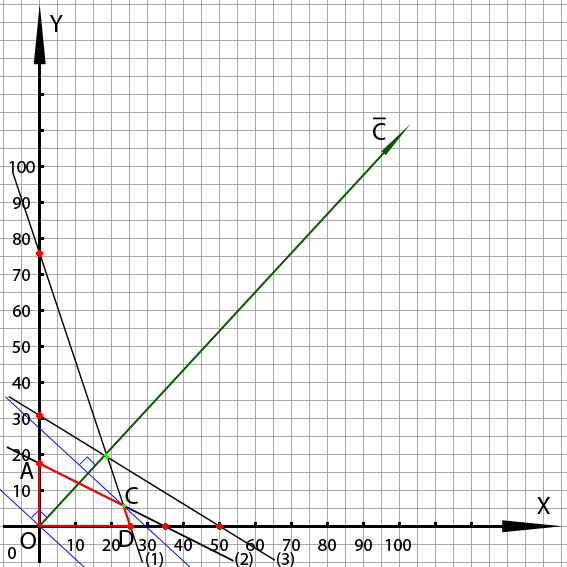
ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ Пусть количество выпускаемой первой продукции – x1, а количество второй – x2, тогда прибыль от продажи всей продукции: F=18x1 + 20x2 → max при условиях: 9x1 + 3x2 ≤ 230; 6x1 + 12x2 ≤ 210; 5x1 + 8x2 ≤ 250; x1 ≥ 0; x2 ≥ 0.
Неравенства заменяем на равенства, x2 заменяем на y. Строим линии ограничений. 1) 9x + 3y1 = 230 y1 = 76,7 - 3x
2) 6x + 12y2 = 210 y2 = 17,5 - 0,5x
3) 5x + 8y3 = 250 y3 = 31,25 - 0,625x
4) x = 0 y = 0 Область допустимых значений - выпуклый многоугольник OACD. Строится направляющий вектор C. Строится перпендикуляр к вектору С через начало координат. Точка С является точкой оптимума. Находим координаты точки оптимума. Приравниваем уравнения 1 и 2. 76,7 - 3x = 17,5 - 0,5x x = 23,68 подставляем x в уравнение: y = 76,7 - 3x y = 5,66
Координаты точки С (23,68; 5,66). Находим значение целевой функции точки оптимума. F(C) = 18*23,68 + 20*5,66 = 426,24 + 113,2 = 539,44 Округлённые результаты (округление в меньшую сторону): F(C) = 18*23 + 20*5 = 514 Ответ: необходимо выпускать 23 единицы первого вида продукции, 5 единиц второго вида продукции, при этом прибыль будет максимальной, и будет равна 514 денежных единиц.
РЕШЕНИЕ СИМПЛЕКС-МЕТОДОМ
Пусть количество выпускаемой первой продукции - x1, а количество второй - x2, тогда прибыль от продажи всей продукции F=18x1 + 20x2 → max при условиях: 9x1 + 3x2 ≤ 230; 6x1 + 12x2 ≤ 210; 5x1 + 8x2 ≤ 250; x1 ≥ 0; x2 ≥ 0. Неравенства заменяем на равенства, вводим искусственные переменные. 9x1 + 3x2 + x3= 230 6x1 + 12x2 + x4= 210 5x1 + 8x2 + x5= 250 Строится исходная симплекс-таблица.
Первая итерация. Ищем генеральный столбец: max (18, 20) = 20 => второй столбец генеральный. Ищем генеральную строку: min Генеральный элемент находится на пересечении второго столбца и второй строки = 12 => заменим x4 на x2. Все элементы генеральной строки(включая свободные члены) делятся на генеральный элемент.
Преобразование строки "Оценки коэффициентов целевой функции": 18 – 20 – 1*20 = 0 0 – 0*20 = 0 0 – 0 – 0*20 = 0 F = 18*0 + 20*17,5 = 350 Базисное решение неоптимально, т.к. имеется положительное значение в строке "Оценки коэффициентов целевой функции". Вторая итерация. Ищем генеральный столбец: max (8, Ищем генеральную строку: min Генеральный элемент находится на пересечении первого столбца и второй строки = 7,5 => заменим x3 на x1. Все элементы генеральной строки(включая свободные члены) делятся на генеральный элемент.
Преобразование строки "Оценки коэффициентов целевой функции": 8 – 1*8 = 0 0 – 0*8 = 0 0
0 – 0*8 = 0 F = 23,67*18+5,665*20 = 426,06 + 113,3 = 539,36 Округлённые результаты (округление в меньшую сторону): F(C) = 23*18 + 5*20 = 514 Ответ: необходимо выпускать 23 единицы первой продукции, 5 единиц второй продукции, при этом прибыль будет максимальной, и будет равна 514 денежных единиц.
|

 =
=  = 17,5 => вторая строка генеральная.
= 17,5 => вторая строка генеральная.

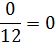

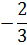
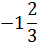
 *3 = 7,5
3 – 1*3 = 1
1 – 0*3 = 1
0 –
*3 = 7,5
3 – 1*3 = 1
1 – 0*3 = 1
0 –  *3 =
*3 =  = –0,25
0 – 0*3 = 0
= –0,25
0 – 0*3 = 0
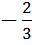 1 – 0*8 = 1
1 – 0*8 = 1
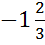
 ) = 8 => первый столбец генеральный.
) = 8 => первый столбец генеральный. =
=  = 23,67 => вторая строка генеральная.
= 23,67 => вторая строка генеральная.






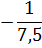

 *0,5 =
*0,5 = 
 *0,5 =
*0,5 =  +
+  =
=  =
= 0,1
0 – 0*0,5 = 0
=
= 0,1
0 – 0*0,5 = 0
 *1 =
*1 =  *1 =
*1 =  =
= 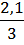 = = –0,7
1 – 0*1 = 1
= = –0,7
1 – 0*1 = 1
 =
= 
 *8 =
*8 =  =
=  = –1,6
= –1,6


