Рост трещины при циклическом нагружении
[1] Она же критическая диаграмма разрушения. Рост трещины при циклическом нагружении
Циклическое нагружение элементов конструкций, как известно, сопровождается повреждением металла от усталости. Усталость приводит сначала к зарождению трещины, обычно в зоне концентрации напряжений или в зоне изначального повреждения поверхности детали. На этот процесс требуется определенное число циклов, которое в стандартных испытаниях на усталость не фиксируется. Факт появления трещины можно установить, только задавшись каким то допуском на ее размер, поэтому число циклов до зарождения трещины можно определить только условно. Затем, зародившаяся трещина растет до полного разрушения. Полное число циклов, состоящее из суммы циклов на зарождение трещины и её распространение, определяет поцикловую долговечность детали. Стадия распространения трещины может занимать значительную долю общей долговечности в зависимости от условий нагружения. Эта доля тем больше, чем более неоднородно внешнее воздействие на деталь, чем более агрессивна окружающая среда. Можно также учитывать, что длительность периода развития трещины зависит от отношения начального коэффициента интенсивности напряжений к критическому. Соответственно этому известный интерес представляет оценка долговечности по числу циклов переменного нагружения на стадии роста трещины (т.е. определение числа циклов при увеличении длины трещины от начального значения l o до критического l c). С теоретической точки зрения изучение параметров, ответственных за процесс роста трещины и входящих в расчетные уравнения, позволяет глубже вникнуть в механическую природу процессов, происходящих в окрестности растущей трещины. С практической точки зрения оценка долговечности важна для приложений, например, при расчете ресурса изделий. Переменность напряжений даже при деформировании в упругой области сопровождается нагревом образца. Наличие трещины локализует область диссипации энергии, сопровождающееся повышением температуры у вершины. Если отвод теплоты затруднен, то это следует принимать во внимание. Для оценки скорости роста усталостных трещин сначала использовали эмпирические формулы, в которые не входили параметры механики разрушения. Введение в число параметров, влияющих на распространение трещины, коэффициента интенсивности напряжений позволило судить об общих закономерностях роста трещины при повторном (циклическом) нагружении. И это естественно, так как рост трещины усталости происходит на фоне упругих деформаций, когда справедливы критерии линейной механики разрушения. С учетом этого было получено довольно много различных зависимостей для скорости роста трещин [17]. Все эти зависимости практически следуют из формулы Париса, которая основана на том, что все явления в кончике трещины, а также поцикловая скорость
Здесь С и n - эмпирические коэффициенты, D К = Кmax – Кmin Многочисленные эксперименты хорошо подтверждают эту формулу, причем показатель степени n для разных материалов располагается в интервале от 2 до 8 (чаще всего n = 2 - 4). Чем больше показатель степени n, тем более хрупкое состояние материала наблюдается при испытании. Обратим внимание на размерность коэффициента С, которая имеет вид м/(МПам0,5)n. Из-за этой неудобной размерности величина С не имеет самостоятельно значения и связана с показателем n соотношением вида Среди многих механических факторов, влияющих на скорость роста усталостных трещин, наибольшая роль принадлежит коэффициенту асимметрии цикла. Известно, что при постоянном D К величина dl/dN растет с ростом R, причем тем в большей степени, чем в более хрупком состоянии находится материал (и чем меньше D К). На рис. 5.14 показано, экспериментально полученное на ферритно-перлитных сталях с содержанием углерода 0,1- 0,2%, падение показателя n и рост коэффициента С с ростом коэффициента асимметрии цикла (на этом рисунке коэффициент С обозначен А). Кроме того, согласно рис. 5.15, видно увеличение скорости роста трещины, при фиксированном размахе коэффициента интенсивности напряжений, с ростом коэффициента асимметрии R).
Рис. 5.14. Изменение характеристик циклической трещиностойкости в формуле Париса с ростом коэффициента асимметрии цикла (В.Н. Минаев)
Рис. 5.15. Увеличение скорости роста трещины с увеличением коэффициента асимметрии цикла для заданного размаха коэффициента интенсивности напряжений
Для учета эффектов, связанных с коэффициентом асимметрии цикла, возможно следующее обобщение формулы Париса:
(С, m – эмпирические величины). При f (R) = 1 - R выражение (5.6.2) переходит в исходную формулу (5.6.1).
Рис. 5.16. Варианты корректирующих функций f (R): (1)
Наилучшее приближение к результатам эксперимента на изгиб алюминиевого сплава дает выражение f (R) = 1-0,5 R -0,5 R2.
Более удобной следует считать модификацию записи формулы Париса в следующем виде:
Удобство состоит в более ясной размерности эмпирических коэффициентов. Формула Париса справедлива для самого протяженного, среднего (линейного в логарифмических шкалах) участка полной диаграммы усталостного разрушения, которая в большинстве случаев имеет S-образный вид (рис. 5.17). Характеристика трещиностойкости Пороговый размах коэффициента интенсивности напряжений
Рис. 5.17. Диаграмма усталостного роста трещины (схема). 1,3 – области низких и высоких скоростей роста трещины; 2 – область справедливости формулы Париса
Рис. 5.18. Зависимость длины трещины от числа циклов
Для описания полной диаграммы усталостного разрушения можно предложить зависимость Яремы-Микитишина [17]
Здесь С 0, q - эмпирические величины, Kth - пороговый коэффициент интенсивности напряжений1, Кfс - вязкость разрушения при доломе (полном разрушении). Как видно из рис. 5.17 на диаграмме усталостного роста трещины можно выделить три участка (области). Первая область припороговая, скорость трещины затухает, приближаясь к скорости линейного участка. Во второй области типично линейное нарастание скорости в логарифмических координатах (степенная в обычных). При расчете долговечности во многих случаях ориентируются только на формулу Париса. Третья область ускоренного нарастания скорости, завершается полным разрушением образца (или детали). На изломе в околопороговой области (первая область на рис. 5.17) наблюдается микросдвиг, в области Париса (вторая область) микроотрыв, в третьей области смешанный механизм разрушения – микросдвиг и микроотрыв, в сочетании с областями статического дорыва. На зависимости длины трещины от числа циклов (рис. 5.18) область Париса ограничена точками, соответствующими При анализе аварийных ситуаций может помочь вид излома, на поверхности которого при циклическом нагружении образуются бороздки, расположенные поперек направления роста трещины. Считают, что, начиная со второй половины диапазона Париса (т.е. после Увеличение частоты нагружения снижает скорость роста трещины. Предполагается, что если Кmax £ Kth, то трещина не растет. Поскольку в процессе циклического нагружения возможно изменение механических свойств материала (даже вдалеке от вершины трещины), то вообще Кfc < КIc (например, Формула (5.6.4) записана для пульсирующего цикла, при коэффициенте асимметрии цикла R = Кmin / Кmax = 0. Кроме того, получила распространение зависимость Формана
Эта формула описывает второй и третий участки диаграммы усталостного разрушения. Обобщение этой формулы позволяет описать всю диаграмму роста трещины (формула В.Н. Минаева)
Здесь
Таблица 5.1 Эмпирические параметры для формулы (5.6.6)
Общий эффект коэффициента асимметрии цикла на деформацию диаграммы усталостного роста трещины схематично можно отразить с помощью сдвигов крайних её точек, как показано на рис. 5.19.
Рис. 5.19. Сдвиги диаграммы циклической трещиностойкости в зависимости от коэффициентов асимметрии цикла
Заметим, что при R £ 0 кинетика распространения трещины слабо зависит от R, что дало повод игнорировать полуцикл сжатия и принимать при этом D К = К mах. Подстановка в эту формулу вместо
позволяет описать рост короткой трещины в зоне концентрации напряжений. В ней характерна высокая скорость роста трещины, которая уменьшается по мере выхода трещины из зоны концентрации и переходит в кривую для больших трещин. Анализ медленного докритического роста трещины позволил Г.П. Черепанову установить следующую зависимость [24]:
где коэффициент Отметим, что на полуцикле снятия нагрузки, перед вершиной трещины возникают остаточные напряжения (из-за пластической деформации). Поэтому трещина при снятии нагрузки не полностью закрывается и не сразу раскрывается при возрастании напряжения на следующем цикле. Для учета этого эффекта В. Элбер предложил модель, согласно которой размах напряжений за цикл
Причем по Элберу коэффициент раскрытия можно взять в виде Все эти формулы применяют как для обычной (многоцикловой) усталости, так и для малоцикловой усталости. Разумеется, это удобно, но в то же время необходимо проявлять осторожность при обращении с эмпирическими коэффициентами. Дело в том, что механизм усталостного явления различен при малоцикловой и многоцикловой усталости. Эти различия могут даже привести к разрыву кривой Веллера (зависимость smах цикла от N) в области ограниченной выносливости. При этом в одном случае трещина идет по телу зерна, в другом - по его границе. Отсюда также видно, что характеристики усталостной прочности должны зависеть от структуры материала. Поэтому возможна зависимость эмпирических коэффициентов от уровня максимальных напряжений цикла. Вместе с тем, имеются экспериментальные данные, что в условиях малоцикловой усталости можно использовать зависимость
где C и m эмпирические постоянные (естественно, не совпадающие аналогичными из формулы Париса). Эта формула на основании (4.6.5) может быть переписана в виде
которая в определенном смысле удобнее предыдущей. Графики, построенные по этим формулам в логарифмическом масштабе, дают прямые линии. Заметим, что жесткое и податливое нагружения при этих испытаниях дают не совпадающие результаты. Циклическое нагружение тела с трещиной при повышенных температурах приводит к увеличению скорости трещины в связи с ползучестью материала. С течением времени, которое ориентировочно равно Например, эксперимент на листовых образцах из алюминиевого сплава АК4-1Т при температуре 4480 К показал коэффициент пропорциональности
Задача 1. Определить число циклов до разрушения в широкой пластине с центральной трещиной. Начальная длина трещины 8 мм. Максимальное напряжение цикла
|

 её распространения, зависят от коэффициента интенсивности напряжений. Эта формула записывается в следующем виде:
её распространения, зависят от коэффициента интенсивности напряжений. Эта формула записывается в следующем виде: (5.6.1)
(5.6.1) - перепад (размах) коэффициента интенсивности напряжений за один цикл нагружения, N - число циклов,
- перепад (размах) коэффициента интенсивности напряжений за один цикл нагружения, N - число циклов,  .
. . Впоследствии формула (5.6.1) заменена на более подходящую, а именно (5.6.3).
. Впоследствии формула (5.6.1) заменена на более подходящую, а именно (5.6.3).

 , (5.6.2)
, (5.6.2) На рис. 5.16 показаны некоторые варианты корректирующих функций f (R).
На рис. 5.16 показаны некоторые варианты корректирующих функций f (R).
 , (2)
, (2)  , (3)
, (3)  , (4)
, (4)  ; точки – данные эксперимента
; точки – данные эксперимента ,
,  (5.6.3)
(5.6.3) определяется при скорости роста трещины равной
определяется при скорости роста трещины равной  м/цикл. Середина области, описываемой формулой Париса, находится при
м/цикл. Середина области, описываемой формулой Париса, находится при  .
. определяют при скорости 10-10 м/цикл. В итоге имеем, по крайней мере, четыре характеристики циклической трещиностойкости
определяют при скорости 10-10 м/цикл. В итоге имеем, по крайней мере, четыре характеристики циклической трещиностойкости 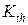 ,
,  ,
,  и
и 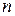 . Поскольку коэффициент асимметрии цикла R известен, то соответственно известны и размахи
. Поскольку коэффициент асимметрии цикла R известен, то соответственно известны и размахи  ,
, 

 Наблюдающиеся отклонения диаграммы от этой формы обычно связаны с непростыми условиями нагружения (активные среды и др.).
Наблюдающиеся отклонения диаграммы от этой формы обычно связаны с непростыми условиями нагружения (активные среды и др.). (5.6.4)
(5.6.4) и
и  , а точка
, а точка  ). Однако в случае недоступности экспериментального определения этих характеристик допустимо считать, что К fс = К Iс (или К с для данной толщины).
). Однако в случае недоступности экспериментального определения этих характеристик допустимо считать, что К fс = К Iс (или К с для данной толщины). (5.6.5)
(5.6.5) . (5.6.6)
. (5.6.6)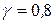 для малоуглеродистых ферритно-перлитных сталей,
для малоуглеродистых ферритно-перлитных сталей,  , а другие эмпирические величины здесь также зависят от коэффициента асимметрии цикла, что видно из табл. 5.1.
, а другие эмпирические величины здесь также зависят от коэффициента асимметрии цикла, что видно из табл. 5.1.






 предела трещиностойкости из (5.1.8), например, при
предела трещиностойкости из (5.1.8), например, при  = q =2,
= q =2,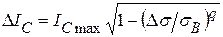 ,
, (5.6.7)
(5.6.7) . В случае, когда K min < 0, в выражении (5.6.7) принимается K min = 0. Эта формула также описывает второй и третий участки диаграммы роста трещины.
. В случае, когда K min < 0, в выражении (5.6.7) принимается K min = 0. Эта формула также описывает второй и третий участки диаграммы роста трещины. выражен через напряжения, при котором трещина начинает раскрываться. Вводится эффективный размах коэффициента интенсивности напряжений в виде (при
выражен через напряжения, при котором трещина начинает раскрываться. Вводится эффективный размах коэффициента интенсивности напряжений в виде (при  )
) , где коэффициент раскрытия
, где коэффициент раскрытия  . Соответственно, формула для скорости роста трещины принимает вид
. Соответственно, формула для скорости роста трещины принимает вид . (5.6.8)
. (5.6.8) .
.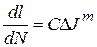
 ,
, (f - частота), к обычной скорости от усталости добавляется поцикловая скорость от ползучести
(f - частота), к обычной скорости от усталости добавляется поцикловая скорость от ползучести  . В первом приближении можно считать, что скорость роста трещины от ползучести v прямо пропорциональна коэффициенту интенсивности напряжений
. В первом приближении можно считать, что скорость роста трещины от ползучести v прямо пропорциональна коэффициенту интенсивности напряжений  . Коэффициент пропорциональности должен быть найден из эксперимента.
. Коэффициент пропорциональности должен быть найден из эксперимента. при толщине образца 2 мм и
при толщине образца 2 мм и 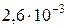 при толщине 1 мм. Из этих данных видно, что увеличение толщины приводит к увеличению скорости трещины.
при толщине 1 мм. Из этих данных видно, что увеличение толщины приводит к увеличению скорости трещины. МПа, коэффициент асимметрии цикла
МПа, коэффициент асимметрии цикла  . Известны константы формулы Париса
. Известны константы формулы Париса  м/МПаm, m = 2. Вязкость разрушения
м/МПаm, m = 2. Вязкость разрушения  .
.


