Предел трещиностойкости как аналог предела прочности
Известен общепринятый факт, что в сложных металлических (особенно сварных) конструкциях несплошности и трещиноподобные дефекты присутствуют, даже после ряда неразрушающих дефектоскопических контролей с соответствующим ремонтом после каждого контроля (см., например, [19]). Поэтому следует признать актуальным и ответственным этап расчета конструкции (определение ее несущей способности) по критериям трещиностойкости на основе статистически достоверного присутствия трещин. Это лежит в основе, так называемого, расчета по допускаемой (и периодически контролируемой) дефектности с подтверждением возможности дальнейшей эксплуатации изделия после дефектоскопического контроля.
Состояние при квазихрупком или вязком разрушении требует иного критериального соотношения, нежели уравнение Ирвина
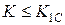 (5.2.1)
(5.2.1)
Существуют несколько критериев разрушения, относящихся к так называемой нелинейной механике разрушения. Можно перечислить наиболее известные – раскрытие в вершине трещины, инвариантный J -интеграл, двухкритериальный подход R6. Однако все они исходят из определенной модели явления разрушения, неизбежно сопряженной с теми или иными ограничениями. И этим ограничениям подвержены также и механические характеристики трещиностойкости, с которыми производятся сравнения расчетных величин для установления факта разрушения.
На наш взгляд гораздо проще, естественнее и нагляднее, а, в конечном счете, и надежнее, ввести в обращение характеристику трещиностойкости (предел трещиностойкости 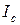 ) по аналогии с пределом прочности (временным сопротивлением) гладкого образца
) по аналогии с пределом прочности (временным сопротивлением) гладкого образца  . Введем понятие - предел трещиностойкости
. Введем понятие - предел трещиностойкости 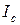 это предел прочности образца с трещиной, представленный коэффициентом интенсивности напряжений.
это предел прочности образца с трещиной, представленный коэффициентом интенсивности напряжений.
Отсюда следует основная идея экспериментального определения предела трещиностойкости. Испытанию подлежит образец с предварительно созданной трещиной. При растяжении (или изгибе) образец с трещиной данной длины доводят до полного разрушения, при этом измеряют только две величины – максимальную силу, выдерживаемую образцом 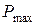 и начальную длину трещины l по излому образца. Возможно использование и критической длины трещины, также определяемой по излому (большей, чем начальная на величину докритического подрастания трещины). Достаточного основания для предпочтения одного варианта другому на настоящее время нет. Никаких дополнительных измерений и приспособлений не требуется. Эти величины -
и начальную длину трещины l по излому образца. Возможно использование и критической длины трещины, также определяемой по излому (большей, чем начальная на величину докритического подрастания трещины). Достаточного основания для предпочтения одного варианта другому на настоящее время нет. Никаких дополнительных измерений и приспособлений не требуется. Эти величины - 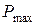 и l – подставляют в формулу для коэффициента интенсивности напряжений K (которая, естественно, известна для данного образца и схемы нагружения) и получают предельный коэффициент интенсивности напряжений, при котором образец ломается.
и l – подставляют в формулу для коэффициента интенсивности напряжений K (которая, естественно, известна для данного образца и схемы нагружения) и получают предельный коэффициент интенсивности напряжений, при котором образец ломается.
Теперь вспомним, что при определении предела прочности совершенно упускается из виду наличие предшествующей, и сопутствующей растяжению, большой пластической деформации. Предел прочности не отражает присутствия пластической деформации образца на момент действия максимальной силы 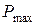 и этой деформацией не интересуются при записи критериального уравнения вида
и этой деформацией не интересуются при записи критериального уравнения вида
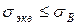 . (5.2.2)
. (5.2.2)
Совершенно аналогично и с пределом трещиностойкости 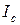 - точно также по
- точно также по 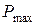 (и длине трещины) определяется коэффициент интенсивности напряжений, не обращая внимания на сопутствующую пластическую деформацию образца на момент достижения
(и длине трещины) определяется коэффициент интенсивности напряжений, не обращая внимания на сопутствующую пластическую деформацию образца на момент достижения 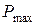 , и этому коэффициенту интенсивности напряжений присваивается название предела трещиностойкости
, и этому коэффициенту интенсивности напряжений присваивается название предела трещиностойкости 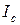 (аналогично, как напряжению при
(аналогично, как напряжению при 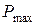 присваивается название временного сопротивления или предела прочности). Тогда расчетное уравнение приобретает вид
присваивается название временного сопротивления или предела прочности). Тогда расчетное уравнение приобретает вид
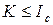 . (5.2.3)
. (5.2.3)
Видно, что это критериальное уравнение схоже по внешнему виду с уравнением (5.2.1), но правая сторона содержит другую механическую характеристику. Уравнение (5.2.3) схоже также и с уравнением (5.2.2): левые стороны в обоих уравнениях одинаковы с точки зрения их вычисления - на основе уравнений теории упругости, а правые схожи тем, что они представляют собой параметры левой части, полученные из эксперимента на момент максимальной несущей способности образцов (независимо от степени пластической деформации).
Для большей наглядности на рис. 5.2 приведены диаграммы деформирования образцов без трещин при определении 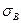 (верхний ряд) и диаграммы деформирования образцов с трещинами при определении
(верхний ряд) и диаграммы деформирования образцов с трещинами при определении 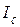 (нижний ряд) [21]. В одном случае по значению
(нижний ряд) [21]. В одном случае по значению 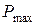 найдено
найдено 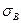 , а в другом по значению
, а в другом по значению 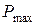 найдено
найдено 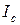 . Видна полная аналогия между характеристиками
. Видна полная аналогия между характеристиками 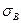 и
и 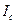 по принципу их получения.
по принципу их получения.
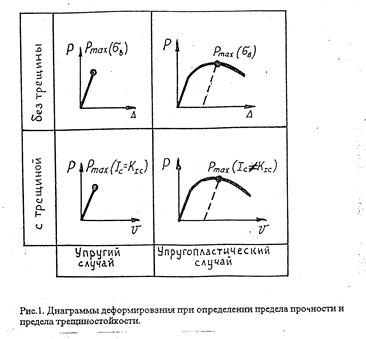
Рис. 5.2. Диаграммы деформирования и предельные характеристики для образцов с трещинами и без них
Теперь важно заметить следующее – поскольку 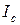 определяется на образцах с трещиной, то длину трещины можно и нужно делать разной. И в этом имеем отличие от предела прочности – если
определяется на образцах с трещиной, то длину трещины можно и нужно делать разной. И в этом имеем отличие от предела прочности – если  есть число, то при определении
есть число, то при определении 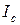 на серии однотипных образцов, но с трещинами разной длины, получаем
на серии однотипных образцов, но с трещинами разной длины, получаем 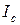 в виде функции длины трещины (поскольку ясно, что
в виде функции длины трещины (поскольку ясно, что 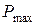 будет разной при трещинах разной длины). Поэтому
будет разной при трещинах разной длины). Поэтому 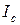 следует определять для некоторого набора длин трещин. Тогда
следует определять для некоторого набора длин трещин. Тогда 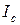 есть не одно число, а набор чисел, т.е. функция. Но, конечно, если указывать конкретную длину трещины, то и величина
есть не одно число, а набор чисел, т.е. функция. Но, конечно, если указывать конкретную длину трещины, то и величина 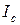 (для этой длины) будет числом. Поэтому значение предела трещиностойкости
(для этой длины) будет числом. Поэтому значение предела трещиностойкости 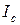 без указания длины трещины утрачивает полезный смысл. Кроме того, поскольку каждой длине трещины соответствует своя сила
без указания длины трещины утрачивает полезный смысл. Кроме того, поскольку каждой длине трещины соответствует своя сила 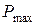 , то, соответственно, каждой длине трещины соответствует и свое разрушающее брутто-напряжение. Поэтому предел трещиностойкости
, то, соответственно, каждой длине трещины соответствует и свое разрушающее брутто-напряжение. Поэтому предел трещиностойкости 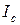 можно представлять не только в виде функции длины трещины (
можно представлять не только в виде функции длины трещины (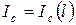 ), но и в функции разрушающего параметра нагрузки
), но и в функции разрушающего параметра нагрузки  (
(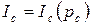 ) или в функции разрушающего номинального напряжения (
) или в функции разрушающего номинального напряжения (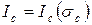 ).
).
Забегая вперед, укажем, что если испытывается не образец, а элемент конструкции, то в качестве параметра нагружения может выступать давление, момент или просто число, пропорционально которому одновременно изменяются приложенные к элементу усилия. В этом принципиальное отличие уравнений вида (5.2.1) и (5.2.2) от уравнения (5.2.3), в котором характеристика материала есть не число, а функция.
В то же время ясно, что в случае хрупкого разрушения 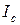 окажется равным
окажется равным 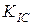 , поскольку пластическая зона пренебрежимо мала. Подстановка
, поскольку пластическая зона пренебрежимо мала. Подстановка 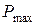 в формулу для коэффициента интенсивности напряжений дает в этом случае величину
в формулу для коэффициента интенсивности напряжений дает в этом случае величину 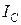 , равную
, равную 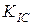 . Получается, что
. Получается, что 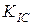 есть частное значение
есть частное значение 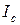 . Но
. Но 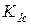 есть фундаментальная характеристика материала – постоянная материала – нахождение которой связано с ограничениями на объем пластической зоны перед вершиной трещины (и с необходимостью специальной оснастки для эксперимента). В то же время,
есть фундаментальная характеристика материала – постоянная материала – нахождение которой связано с ограничениями на объем пластической зоны перед вершиной трещины (и с необходимостью специальной оснастки для эксперимента). В то же время, 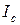 - переменная величина, справедливая при любых размерах и форме пластической зоны. Следовательно, характеристика
- переменная величина, справедливая при любых размерах и форме пластической зоны. Следовательно, характеристика 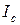 годна для описания не только квазихрупкого разрушения, но и вязкого, причем при трещинах любой длины, включая очень короткие и даже вариант без трещины. В последнем случае уравнение (5.2.3) вырождается в уравнение (5.2.2).
годна для описания не только квазихрупкого разрушения, но и вязкого, причем при трещинах любой длины, включая очень короткие и даже вариант без трещины. В последнем случае уравнение (5.2.3) вырождается в уравнение (5.2.2).
Таким образом, расчет по 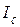 (уравнение (5.2.3)) универсален, он справедлив при любых видах разрушения, при ясной методике экспериментального определения характеристики трещиностойкости
(уравнение (5.2.3)) универсален, он справедлив при любых видах разрушения, при ясной методике экспериментального определения характеристики трещиностойкости 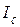 , не сопровождаемой ограничениями на пластическое течение в нетто-сечении образца.
, не сопровождаемой ограничениями на пластическое течение в нетто-сечении образца.
Поясним вопрос об использовании в расчетном уравнении (5.2.3) механической характеристики в виде функции. Уравнение (5.1.3) можно записать либо так
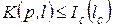 , (5.2.4)
, (5.2.4)
либо так
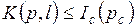 , (5.2.5)
, (5.2.5)
где p – параметр нагрузки (это, как уже указывалось, может быть действующее в растянутом образце брутто-напряжение, при разрушении оно равно 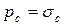 ; либо приложенная к образцу сила или изгибающий момент, либо внутреннее давление, если образец представляет собой отрезок трубы). Например, если в брутто-сечении действуют неравномерные (в направлении оси х) напряжения, то они могут быть записаны в виде
; либо приложенная к образцу сила или изгибающий момент, либо внутреннее давление, если образец представляет собой отрезок трубы). Например, если в брутто-сечении действуют неравномерные (в направлении оси х) напряжения, то они могут быть записаны в виде 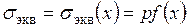 ; т.е. не надо думать, что опасное состояние определяется только местным напряжением в какой-то одной точке. Нет, это состояние может глобально определяться силой, моментом и пр., что отражено параметром нагрузки.
; т.е. не надо думать, что опасное состояние определяется только местным напряжением в какой-то одной точке. Нет, это состояние может глобально определяться силой, моментом и пр., что отражено параметром нагрузки.
Проводя эксперимент по определению 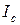 на серии образцов с разными длинами трещин (рис. 5.3), вначале получаем пары чисел
на серии образцов с разными длинами трещин (рис. 5.3), вначале получаем пары чисел 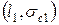 ,
, 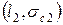 ,
, 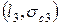 , …,. Откладывая эти разрушающие напряжения в зависимости от длины трещины, получаем диаграмму остаточной прочности[1] в координатах
, …,. Откладывая эти разрушающие напряжения в зависимости от длины трещины, получаем диаграмму остаточной прочности[1] в координатах 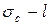 (с правой стороны на рис. 5.3). Такие диаграммы часто имеют самостоятельное значение и интерес и широко используются, например, в авиации. Для наших целей эти пары экспериментальных точек
(с правой стороны на рис. 5.3). Такие диаграммы часто имеют самостоятельное значение и интерес и широко используются, например, в авиации. Для наших целей эти пары экспериментальных точек 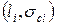 можно использовать для расчета коэффициента интенсивности напряжений
можно использовать для расчета коэффициента интенсивности напряжений 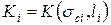 и по определению эти предельные (т.е. в момент разрушения) коэффициенты интенсивности напряжений и есть набор пределов трещиностойкости
и по определению эти предельные (т.е. в момент разрушения) коэффициенты интенсивности напряжений и есть набор пределов трещиностойкости 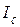 для образцов с разными длинами трещин
для образцов с разными длинами трещин 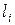 .
.
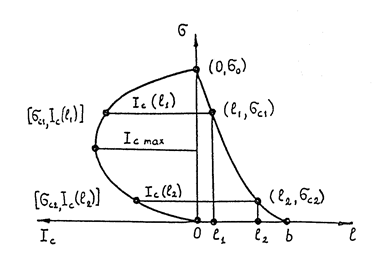
Рис. 5.3. Схема диаграмм остаточной прочности (справа) и трещиностойкости (слева)
Предел трещиностойкости удобно изобразить графически на плоскости с координатами 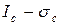 . Это и наглядно, и позволяет проводить графоаналитический расчет на прочность. На рис. 5.3 схематически справа от оси ординат отложены экспериментальные точки остаточной прочности
. Это и наглядно, и позволяет проводить графоаналитический расчет на прочность. На рис. 5.3 схематически справа от оси ординат отложены экспериментальные точки остаточной прочности 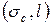 . Каждой длине трещины образца соответствует свое разрушающее напряжение
. Каждой длине трещины образца соответствует свое разрушающее напряжение 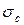 . Подстановка этих двух экспериментальных величин в формулу для коэффициента интенсивности напряжений данного образца дает точки с координатами
. Подстановка этих двух экспериментальных величин в формулу для коэффициента интенсивности напряжений данного образца дает точки с координатами 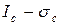 , которые отложены слева от оси ординат. Каждой точке с координатами
, которые отложены слева от оси ординат. Каждой точке с координатами 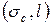 справа соответствует точка с координатами
справа соответствует точка с координатами 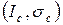 слева. Если через экспериментальные точки справа провести линию, то это будет диаграмма остаточной прочности, т.е. график
слева. Если через экспериментальные точки справа провести линию, то это будет диаграмма остаточной прочности, т.е. график 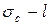 . Если через точки слева провести линию, то это будет диаграмма трещиностойкости, т.е. график
. Если через точки слева провести линию, то это будет диаграмма трещиностойкости, т.е. график 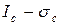 .
.
Получилось, что диаграмма трещиностойкости построена с помощью пределов трещиностойкости, и каждая ордината на этой диаграмме есть предел трещиностойкости для соответствующего разрушающего напряжения 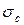 , а, следовательно, и для соответствующей длины трещины l c. Именно поэтому, желательно исходные экспериментальные данные представлять в виде сдвоенного графика с одной осью координат
, а, следовательно, и для соответствующей длины трещины l c. Именно поэтому, желательно исходные экспериментальные данные представлять в виде сдвоенного графика с одной осью координат 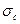 (общей для обоих графиков) и с разными осями
(общей для обоих графиков) и с разными осями 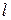 и
и 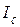 , направленными в разные стороны.
, направленными в разные стороны.
Полученная экспериментально диаграмма трещиностойкости в координатах 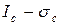 (или
(или 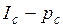 ) может служить как для оценки материала (при условии, что она получена на образцах стандартной геометрии), так и для расчетов прочности деталей, схожих по геометрии и схеме нагружения с образцом.
) может служить как для оценки материала (при условии, что она получена на образцах стандартной геометрии), так и для расчетов прочности деталей, схожих по геометрии и схеме нагружения с образцом.
Диаграмма трещиностойкости ограничивает область допустимых состояний, которые оцениваются коэффициентами интенсивности напряжений. Допустимые состояния представлены точками с координатами 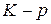 внутри диаграммы (слева на рис. 5.3). Чем больше эта область (особенно в диапазоне малых трещин), тем более трещиностойкий материал и другие параметры, подлежащие сопоставлению. Границу области допустимых состояний (диаграмму трещиностойкости) можно аппроксимировать уравнением
внутри диаграммы (слева на рис. 5.3). Чем больше эта область (особенно в диапазоне малых трещин), тем более трещиностойкий материал и другие параметры, подлежащие сопоставлению. Границу области допустимых состояний (диаграмму трещиностойкости) можно аппроксимировать уравнением
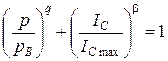 . (5.2.6)
. (5.2.6)
Здесь 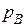 - параметр нагрузки при разрушении без трещины,
- параметр нагрузки при разрушении без трещины, 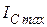 - максимум функции
- максимум функции 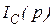 или
или 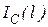 ,
, 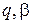 - эмпирические числа.
- эмпирические числа.
Из этого уравнения вытекает более привычная запись критериального уравнения
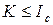 , (5.2.7)
, (5.2.7)
где 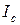 - предел трещиностойкости, аналитическое выражение которого, полученное из уравнения (5.2.6), выглядит так
- предел трещиностойкости, аналитическое выражение которого, полученное из уравнения (5.2.6), выглядит так
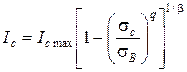 . (5.2.8)
. (5.2.8)
Из уравнения (5.2.6) можно также получить уравнение диаграммы остаточной прочности (для разрушающего параметра нагрузки в функции длины трещины) при 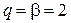
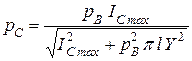 . (5.2.9)
. (5.2.9)
и предел трещиностойкости 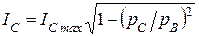 , где на основании экспериментов вместо квадрата под корнем предпочтительнее поставить четвертую степень. Здесь
, где на основании экспериментов вместо квадрата под корнем предпочтительнее поставить четвертую степень. Здесь 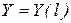 - геометрический фактор (К - тарировка) в выражении
- геометрический фактор (К - тарировка) в выражении 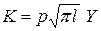 .
.
Если принять 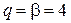 , то
, то
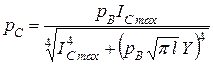 . (5.2.10)
. (5.2.10)
Если 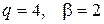 , то
, то
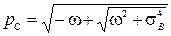 ,
, 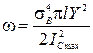 . (5.2.11)
. (5.2.11)
Немногочисленные пока эксперименты для тонкостенных конструкций дают 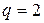 , а для массивных -
, а для массивных - 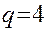 ; при этом
; при этом 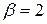 .
.
Эксперименты на трех марках сталей (рис. 5.3) дали лучшее соответствие с уравнением (5.2.8) при 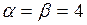 [20]. В таком случае из уравнения (5.2.8) запишем аппроксимирующее выражение для предела трещиностойкости
[20]. В таком случае из уравнения (5.2.8) запишем аппроксимирующее выражение для предела трещиностойкости
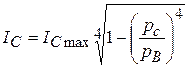 . (5.2.12)
. (5.2.12)
На рис. 5.4 по оси ординат предел трещиностойкости дан в безразмерном виде 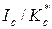 (где
(где 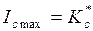 по ГОСТ 25.506-85), а по оси абсцисс разрушающее брутто-напряжение
по ГОСТ 25.506-85), а по оси абсцисс разрушающее брутто-напряжение 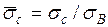 .
.
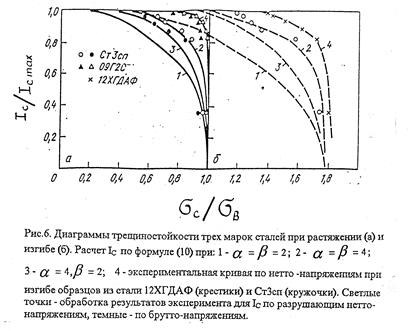
Рис. 5.4. Диаграммы трещиностойкости трех марок стали при растяжении (а) и изгибе (б). Расчет I C по формуле (5.1.8) при: 1 - 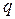 =
= 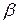 =2; 2 -
=2; 2 - 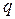 =
= 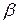 =4; 3 -
=4; 3 - 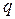 =4,
=4, 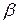 =2; 4 – экспериментальная кривая по нетто-напряжениям при изгибе образцов из стали 12ХГДАФ (крестики) и Ст3сп (кружочки). Светлые точки – обработка результатов экспериментов для I C по разрушающим нетто-напряжениям, темные – по брутто-напряжениям
=2; 4 – экспериментальная кривая по нетто-напряжениям при изгибе образцов из стали 12ХГДАФ (крестики) и Ст3сп (кружочки). Светлые точки – обработка результатов экспериментов для I C по разрушающим нетто-напряжениям, темные – по брутто-напряжениям
Приведем в безразмерном виде графики зависимости предела трещиностойкости от разрушающего напряжения (диаграмм трещиностойкости) при разных показателях степени 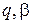 (рис. 5.5). Их взаимное визуальное сопоставление позволяет рекомендовать вариант
(рис. 5.5). Их взаимное визуальное сопоставление позволяет рекомендовать вариант 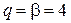 . В этом варианте промежуточная область между критериями
. В этом варианте промежуточная область между критериями 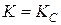 и
и 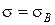 минимальна. Минимальность имеется в виду с точки зрения минимальности диапазона длин трещин, в котором оба записанных критерия не действительны.
минимальна. Минимальность имеется в виду с точки зрения минимальности диапазона длин трещин, в котором оба записанных критерия не действительны.
Рис. 5.5. Диаграммы трещиностойкости: сплошная линия 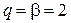 , точечная
, точечная 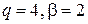 , штриховая
, штриховая 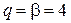
Заметим здесь же, что при отсутствии специальных экспериментов, величину 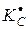 , определяемой согласно ГОСТ 25.506-85, можно принять равной
, определяемой согласно ГОСТ 25.506-85, можно принять равной 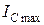 , хотя и определяется при фиксированной длине трещины
, хотя и определяется при фиксированной длине трещины 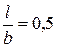 .
.
Покажем на примере растянутого плоского образца с центральной трещиной, как с изменением длины трещины меняется разрушающий коэффициент интенсивности напряжений (рис. 5.6). При малой длине трещины (в сравнении с шириной образца) и при большой длине трещины имеем вязкое разрушение, падение разрушающих напряжений (в сравнении с теми, что следуют из критерия Ирвина) и, соответственно, уменьшаются разрушающие коэффициенты интенсивности напряжений, названные теперь пределами трещиностойкости. Для средних длин трещин имеем хрупкое разрушение.
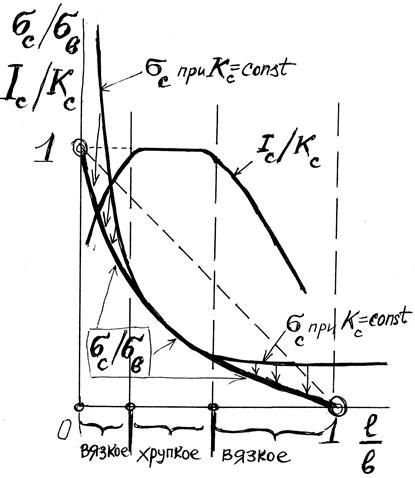
Рис. 5.6. Диапазоны хрупких и вязких состояний при растяжении плоского образца с трещиной
Это область длин трещин, принятая в нормативных документах как наиболее вероятная для обеспечения хрупкого состояния образца с целью определения вязкости разрушения. В этой области длин трещин разрушающие коэффициенты интенсивности напряжений (т.е. пределы трещиностойкости) наибольшие. Отсюда видна ориентировочная оценка – при малых длинах трещин или при малых перемычках между концом трещины и свободной стороной пластины, в случае вязкого состояния, можно ограничиться расчетом по пределу прочности.
[1] Она же критическая диаграмма разрушения.

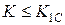 (5.2.1)
(5.2.1)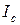 ) по аналогии с пределом прочности (временным сопротивлением) гладкого образца
) по аналогии с пределом прочности (временным сопротивлением) гладкого образца  . Введем понятие - предел трещиностойкости
. Введем понятие - предел трещиностойкости 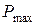 и начальную длину трещины l по излому образца. Возможно использование и критической длины трещины, также определяемой по излому (большей, чем начальная на величину докритического подрастания трещины). Достаточного основания для предпочтения одного варианта другому на настоящее время нет. Никаких дополнительных измерений и приспособлений не требуется. Эти величины -
и начальную длину трещины l по излому образца. Возможно использование и критической длины трещины, также определяемой по излому (большей, чем начальная на величину докритического подрастания трещины). Достаточного основания для предпочтения одного варианта другому на настоящее время нет. Никаких дополнительных измерений и приспособлений не требуется. Эти величины - 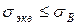 . (5.2.2)
. (5.2.2)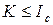 . (5.2.3)
. (5.2.3)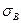 (верхний ряд) и диаграммы деформирования образцов с трещинами при определении
(верхний ряд) и диаграммы деформирования образцов с трещинами при определении 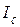 (нижний ряд) [21]. В одном случае по значению
(нижний ряд) [21]. В одном случае по значению 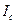 по принципу их получения.
по принципу их получения.
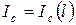 ), но и в функции разрушающего параметра нагрузки
), но и в функции разрушающего параметра нагрузки  (
(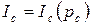 ) или в функции разрушающего номинального напряжения (
) или в функции разрушающего номинального напряжения (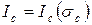 ).
).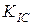 , поскольку пластическая зона пренебрежимо мала. Подстановка
, поскольку пластическая зона пренебрежимо мала. Подстановка 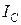 , равную
, равную 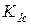 есть фундаментальная характеристика материала – постоянная материала – нахождение которой связано с ограничениями на объем пластической зоны перед вершиной трещины (и с необходимостью специальной оснастки для эксперимента). В то же время,
есть фундаментальная характеристика материала – постоянная материала – нахождение которой связано с ограничениями на объем пластической зоны перед вершиной трещины (и с необходимостью специальной оснастки для эксперимента). В то же время, 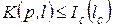 , (5.2.4)
, (5.2.4)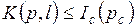 , (5.2.5)
, (5.2.5)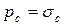 ; либо приложенная к образцу сила или изгибающий момент, либо внутреннее давление, если образец представляет собой отрезок трубы). Например, если в брутто-сечении действуют неравномерные (в направлении оси х) напряжения, то они могут быть записаны в виде
; либо приложенная к образцу сила или изгибающий момент, либо внутреннее давление, если образец представляет собой отрезок трубы). Например, если в брутто-сечении действуют неравномерные (в направлении оси х) напряжения, то они могут быть записаны в виде 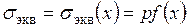 ; т.е. не надо думать, что опасное состояние определяется только местным напряжением в какой-то одной точке. Нет, это состояние может глобально определяться силой, моментом и пр., что отражено параметром нагрузки.
; т.е. не надо думать, что опасное состояние определяется только местным напряжением в какой-то одной точке. Нет, это состояние может глобально определяться силой, моментом и пр., что отражено параметром нагрузки.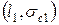 ,
, 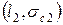 ,
, 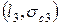 , …,. Откладывая эти разрушающие напряжения в зависимости от длины трещины, получаем диаграмму остаточной прочности[1] в координатах
, …,. Откладывая эти разрушающие напряжения в зависимости от длины трещины, получаем диаграмму остаточной прочности[1] в координатах 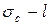 (с правой стороны на рис. 5.3). Такие диаграммы часто имеют самостоятельное значение и интерес и широко используются, например, в авиации. Для наших целей эти пары экспериментальных точек
(с правой стороны на рис. 5.3). Такие диаграммы часто имеют самостоятельное значение и интерес и широко используются, например, в авиации. Для наших целей эти пары экспериментальных точек 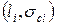 можно использовать для расчета коэффициента интенсивности напряжений
можно использовать для расчета коэффициента интенсивности напряжений 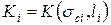 и по определению эти предельные (т.е. в момент разрушения) коэффициенты интенсивности напряжений и есть набор пределов трещиностойкости
и по определению эти предельные (т.е. в момент разрушения) коэффициенты интенсивности напряжений и есть набор пределов трещиностойкости 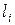 .
.
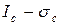 . Это и наглядно, и позволяет проводить графоаналитический расчет на прочность. На рис. 5.3 схематически справа от оси ординат отложены экспериментальные точки остаточной прочности
. Это и наглядно, и позволяет проводить графоаналитический расчет на прочность. На рис. 5.3 схематически справа от оси ординат отложены экспериментальные точки остаточной прочности 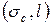 . Каждой длине трещины образца соответствует свое разрушающее напряжение
. Каждой длине трещины образца соответствует свое разрушающее напряжение 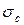 . Подстановка этих двух экспериментальных величин в формулу для коэффициента интенсивности напряжений данного образца дает точки с координатами
. Подстановка этих двух экспериментальных величин в формулу для коэффициента интенсивности напряжений данного образца дает точки с координатами 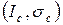 слева. Если через экспериментальные точки справа провести линию, то это будет диаграмма остаточной прочности, т.е. график
слева. Если через экспериментальные точки справа провести линию, то это будет диаграмма остаточной прочности, т.е. график 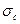 (общей для обоих графиков) и с разными осями
(общей для обоих графиков) и с разными осями 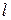 и
и 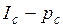 ) может служить как для оценки материала (при условии, что она получена на образцах стандартной геометрии), так и для расчетов прочности деталей, схожих по геометрии и схеме нагружения с образцом.
) может служить как для оценки материала (при условии, что она получена на образцах стандартной геометрии), так и для расчетов прочности деталей, схожих по геометрии и схеме нагружения с образцом.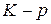 внутри диаграммы (слева на рис. 5.3). Чем больше эта область (особенно в диапазоне малых трещин), тем более трещиностойкий материал и другие параметры, подлежащие сопоставлению. Границу области допустимых состояний (диаграмму трещиностойкости) можно аппроксимировать уравнением
внутри диаграммы (слева на рис. 5.3). Чем больше эта область (особенно в диапазоне малых трещин), тем более трещиностойкий материал и другие параметры, подлежащие сопоставлению. Границу области допустимых состояний (диаграмму трещиностойкости) можно аппроксимировать уравнением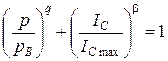 . (5.2.6)
. (5.2.6)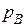 - параметр нагрузки при разрушении без трещины,
- параметр нагрузки при разрушении без трещины, 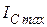 - максимум функции
- максимум функции 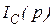 или
или 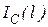 ,
, 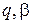 - эмпирические числа.
- эмпирические числа.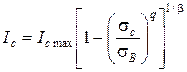 . (5.2.8)
. (5.2.8)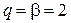
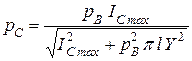 . (5.2.9)
. (5.2.9)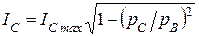 , где на основании экспериментов вместо квадрата под корнем предпочтительнее поставить четвертую степень. Здесь
, где на основании экспериментов вместо квадрата под корнем предпочтительнее поставить четвертую степень. Здесь 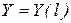 - геометрический фактор (К - тарировка) в выражении
- геометрический фактор (К - тарировка) в выражении 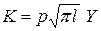 .
.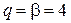 , то
, то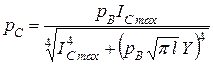 . (5.2.10)
. (5.2.10)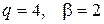 , то
, то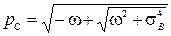 ,
, 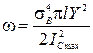 . (5.2.11)
. (5.2.11)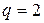 , а для массивных -
, а для массивных - 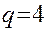 ; при этом
; при этом 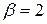 .
.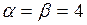 [20]. В таком случае из уравнения (5.2.8) запишем аппроксимирующее выражение для предела трещиностойкости
[20]. В таком случае из уравнения (5.2.8) запишем аппроксимирующее выражение для предела трещиностойкости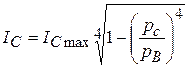 . (5.2.12)
. (5.2.12)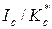 (где
(где 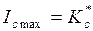 по ГОСТ 25.506-85), а по оси абсцисс разрушающее брутто-напряжение
по ГОСТ 25.506-85), а по оси абсцисс разрушающее брутто-напряжение 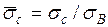 .
.
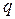 =
= 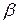 =2; 2 -
=2; 2 - 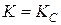 и
и 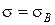 минимальна. Минимальность имеется в виду с точки зрения минимальности диапазона длин трещин, в котором оба записанных критерия не действительны.
минимальна. Минимальность имеется в виду с точки зрения минимальности диапазона длин трещин, в котором оба записанных критерия не действительны.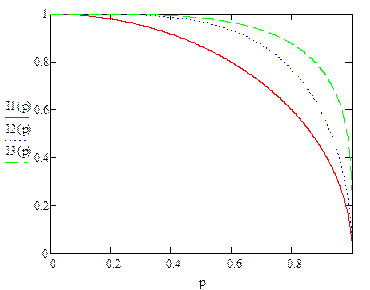
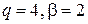 , штриховая
, штриховая 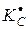 , определяемой согласно ГОСТ 25.506-85, можно принять равной
, определяемой согласно ГОСТ 25.506-85, можно принять равной 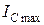 , хотя и определяется при фиксированной длине трещины
, хотя и определяется при фиксированной длине трещины 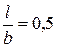 .
.



