Двухпараметрические критерии разрушения
Введите в форму фамилию и имя вновь прибывшего читателя (читателя, которого нет в списках таблицы Читатели). Закройте форму. Откройте таблицу Читатели и оцените результат. Введите все недостающие данные по этому читателю. Оценка несущей способности металлических конструкций с трещинами Двухпараметрические критерии разрушения Двухпараметрический критерий разрушения объединяет одним уравнением два разных критерия. Суть двухпараметрических критериев можно проследить на следующем схематическом примере. Рассмотрим следующие два критерия. Обычный в сопротивлении материалов критерий недопущения пластических деформаций при растяжении детали без трещины
Рис. 5.1. Критическая диаграмма разрушения (а) и диаграмма трещиностойкости (в)
гиперболы на рис. 5.1, а коэффициент интенсивности напряжений один и тот же и равен константе На основании линейной теории упругости Диаграмма на рис. 5.1, в получила название диаграммы трещиностойкости (failure assessment diagram - FAD). Таким образом, два критерия наступления предельных состояний отражены одной линией на диаграмме трещиностойкости. Далее будет рассмотрен двухпараметрический критерий, основанный на понятии предела трещиностойкости (ultimate crack resistance), как экспериментальной характеристики, получаемой в виде коэффициента интенсивности напряжений по максимальной силе, выдерживаемой образцами с разными длинами трещин.
[1] Обычно коэффициент интенсивности напряжений рассчитывают по брутто-напряжению
|

 . Критерий недопущения в детали неуправляемого роста трещины
. Критерий недопущения в детали неуправляемого роста трещины  (если она есть). В последнем уравнении (при знаке равенства) разрушающее напряжение стремится к бесконечности при уменьшении длины трещины. Это противоречит опыту. Поэтому, на основании первого критерия, отрежем гиперболу второго критерия на уровне предела текучести (рис. 5.1, а). На этом рисунке построена критическая диаграмма разрушения на плоскости «предельное напряжение
(если она есть). В последнем уравнении (при знаке равенства) разрушающее напряжение стремится к бесконечности при уменьшении длины трещины. Это противоречит опыту. Поэтому, на основании первого критерия, отрежем гиперболу второго критерия на уровне предела текучести (рис. 5.1, а). На этом рисунке построена критическая диаграмма разрушения на плоскости «предельное напряжение  - полудлина трещины
- полудлина трещины  ». Для каждой точки
». Для каждой точки
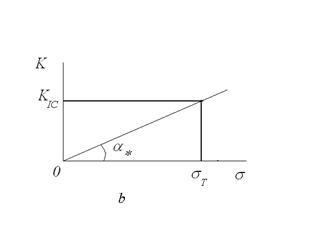
 . Эту константу отложим на графике (рис. 5.1, в) в координатах «коэффициент интенсивности напряжений К – действующее напряжение
. Эту константу отложим на графике (рис. 5.1, в) в координатах «коэффициент интенсивности напряжений К – действующее напряжение  .
.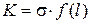 , и функция
, и функция  представляет собой угловой коэффициент прямой из начала координат, т.е.
представляет собой угловой коэффициент прямой из начала координат, т.е.  . Если трещины нет, то
. Если трещины нет, то  . Увеличение длины трещины приводит к увеличению угла наклона луча из начала координат
. Увеличение длины трещины приводит к увеличению угла наклона луча из начала координат  . Точка пересечения этого луча с линиями
. Точка пересечения этого луча с линиями  и
и  отражает наступление предельного состояния по тому или иному критерию. Линия
отражает наступление предельного состояния по тому или иному критерию. Линия  разделяет области разных предельных состояний. Рис. 5.1, а показывает, что предельное напряжение при длине больше
разделяет области разных предельных состояний. Рис. 5.1, а показывает, что предельное напряжение при длине больше  будет разрушающим по критерию Ирвина, а при длине трещины меньше
будет разрушающим по критерию Ирвина, а при длине трещины меньше 


