Вероятность безотказной работы
Среди возможных принципов определения прочностной надежности и ресурса (долговечности) конструкции, наряду с детерминистическими, существуют вероятностные методы. Это определяется тем, что многие величины (нагрузки, размеры и т.п.), участвующие в расчетах случайные. Поэтому их можно описать статистическими методами. Прочностную надежность можно количественно определить в виде вероятности безотказной работы Р. Вероятность отказа Q соответствует противоположному событию, поэтому  . Желательно, чтобы вероятность безотказной работы была близка к единице. Она и равна единице, когда деталь или конструкция только что изготовлены. Но в эксплуатации, с течением времени, из-за многих, скрытых от нас факторов, возможность нарушения прочности нарастает, и вероятность безотказной работы падает. При этом вероятность отказа со временем t увеличивается так, что в каждый момент времени
. Желательно, чтобы вероятность безотказной работы была близка к единице. Она и равна единице, когда деталь или конструкция только что изготовлены. Но в эксплуатации, с течением времени, из-за многих, скрытых от нас факторов, возможность нарушения прочности нарастает, и вероятность безотказной работы падает. При этом вероятность отказа со временем t увеличивается так, что в каждый момент времени  . Прочность конструкции (детали) с определенной вероятностью сохраняется при условии, что
. Прочность конструкции (детали) с определенной вероятностью сохраняется при условии, что
 , (1)
, (1)
где  - нижний предел вероятности безотказной работы, это допускаемая вероятность, аналогично допускаемому напряжению в сопротивлении материалов. Часто вместо
- нижний предел вероятности безотказной работы, это допускаемая вероятность, аналогично допускаемому напряжению в сопротивлении материалов. Часто вместо  вводят обозначение
вводят обозначение  . Когда через какое-то время вероятность безотказной работы опустится до величины
. Когда через какое-то время вероятность безотказной работы опустится до величины  , то это время и есть ресурс (гамма-процентный ресурс[1]). Эксплуатация конструкции должна быть прекращена (или произведен ремонт для восстановления работоспособного состояния). Гамма-процентный ресурс Т находят как корень уравнения
, то это время и есть ресурс (гамма-процентный ресурс[1]). Эксплуатация конструкции должна быть прекращена (или произведен ремонт для восстановления работоспособного состояния). Гамма-процентный ресурс Т находят как корень уравнения 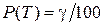 .
.
Как любая случайная величина напряжение  и прочность R характеризуются плотностью распределения их вероятности
и прочность R характеризуются плотностью распределения их вероятности  и
и  . Площадь (заштрихована на рис. 5.37) под кривыми плотностей в области их перекрытия равна вероятности отказа, при котором
. Площадь (заштрихована на рис. 5.37) под кривыми плотностей в области их перекрытия равна вероятности отказа, при котором  . В области
. В области
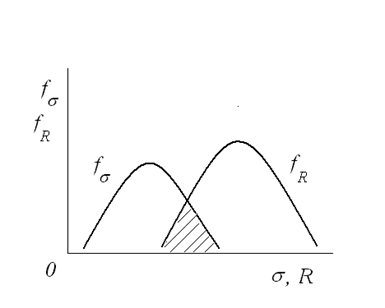
Рис. 5.37. Перекрытие плотности вероятности напряжений и прочности
перекрытия вероятность попадания некоторого напряжения  в интервал
в интервал  равна
равна  . Вероятность того, что прочность выше напряжения
. Вероятность того, что прочность выше напряжения  равна
равна  . Вероятность того, что одновременно напряжение
. Вероятность того, что одновременно напряжение  находится в интервале
находится в интервале  и прочность выше
и прочность выше  равна
равна 
 . Если это соблюдается для всех напряжений
. Если это соблюдается для всех напряжений  , то это и будет вероятность безотказной работы, т.е.
, то это и будет вероятность безотказной работы, т.е.
 (2)
(2)
Получим отсюда вероятность отказа, учитывая, что 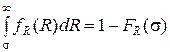
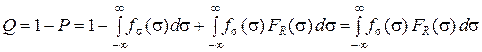 (3)
(3)
Аналогично можно получить вероятность безотказной работы, полагая, что напряжение меньше прочности. Тогда
 (4)
(4)
Отсюда найдем вероятность отказа
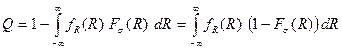 (5)
(5)
Здесь  и
и 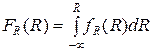 - функции распределения вероятности напряжений и прочности. Записанные формулы предполагают бесконечные «хвосты» у распределений. Если области распределения плотности напряжений и прочности ограничены, то это следует учесть в пределах интегрирования.
- функции распределения вероятности напряжений и прочности. Записанные формулы предполагают бесконечные «хвосты» у распределений. Если области распределения плотности напряжений и прочности ограничены, то это следует учесть в пределах интегрирования.
Задача 1. Дано постоянное распределение напряжений на интервале 80-140 МПа и прочности на интервале 100-200 МПа. Найти Р.
Решение. Площадь под графиком плотности вероятности равна единице. Отсюда  1/МПа и
1/МПа и  1/МПа. По формуле (2) находим вероятность безотказной работы
1/МПа. По формуле (2) находим вероятность безотказной работы
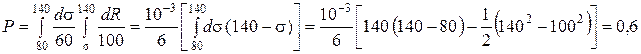
Итак, при таких распределениях надежность конструкции составляет 60%. Обратим внимание на пределы интегрирования – напряжений нет выше 140 МПа, а распределение прочности начинается со 100 МПа.
Найдем для этой же задачи вероятность отказа по площади перехлеста графиков плотностей (заштрихована на рис. 5.38). Эта площадь равна вероятности того, что прочность меньше 40 МПа.
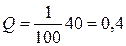 . Результат согласуется с полученной вероятностью Р.
. Результат согласуется с полученной вероятностью Р.
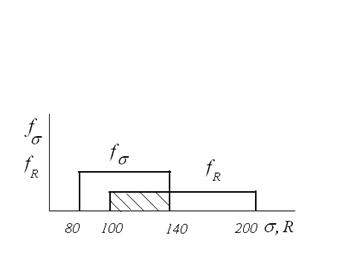
Рис. 5.38. Постоянное распределение напряжений и прочности
Формулу (2) можно преобразовать следующим образом. Входящий в неё внутренний интеграл обозначим символом  , причем
, причем 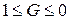 . Остальную часть под интегралом обозначим
. Остальную часть под интегралом обозначим 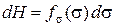 . Тогда
. Тогда  , причем
, причем  . В итоге вероятность безотказной работы примет вид
. В итоге вероятность безотказной работы примет вид
 . (6)
. (6)
Получили, что вероятность безотказной работы равна площади под графиком функции G от H. Эту формулу удобно использовать в случае экспериментальных точек.
Задача 2. Экспериментально замеренные напряжения расположим в виде возрастающей последовательности 134, 145, 162, 175, 184, 198, 218, 238, 256, 274, 290, 310 МПа. Экспериментально замеренная прочность 210, 224, 243, 262, 286, 322, 348, 362 МПа. Определить вероятность безотказной работы.
Решение. Воспользуемся графическим способом на основе формулы (6). Сначала построим функции распределения по экспериментальным точкам. Для напряжений 12 точек. Поскольку функция распределения изменяется от нуля до единицы, то эти 12 напряжений возрастают от нуля до единицы шагами равными 1/12 = 0,08. Координаты точек функции распределения напряжений таковы

|
|
|
|
|
|
|
|
|
|
|
|
|

| 0,08
| 0,16
| 0,25
| 0,33
| 0,41
| 0,5
| 0,58
| 0,66
| 0,75
| 0,83
| 0,91
|
|
По этим точкам можно построить график функции распределения и через точки провести аппроксимирующую линию с тем, чтобы в дальнейшем её использовать для определения значений функции распределения.
Аналогично находим координаты точек функции распределения прочности шагами 1/8 = 0,125.

|
|
|
|
|
|
|
|
|
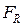
| 0,125
| 0,25
| 0,375
| 0,5
| 0,625
| 0,75
| 0,825
|
|
Теперь находим функции  и
и  .
.

|
|
|
|
|
|
|
|
|
|

|
| 0,24
| 0,55
| 0,71
| 0,81
| 0,92
|
|
|
|

|
|
| 0,875
| 0,565
| 0,444
| 0,347
| 0,289
| 0,188
|
|
По полученным координатам строим график  , показанный на рис. 5.39. Площадь под этим графиком дает вероятность безотказной работы, которая после подсчета оказывается равной Р = 0,76.
, показанный на рис. 5.39. Площадь под этим графиком дает вероятность безотказной работы, которая после подсчета оказывается равной Р = 0,76.
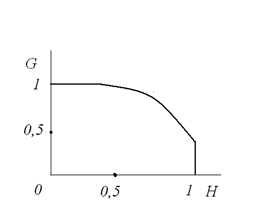
Рис. 5.39. График вспомогательной функции для подсчета вероятности безотказной работы по экспериментальным данным
При нормальном распределении напряжений с плотностью вероятности  и прочности с плотностью
и прочности с плотностью  можно использовать их композицию. Это сумма Z двух случайных величин, которая тоже будет случайной величиной с нормальным распределением, с плотностью вероятности
можно использовать их композицию. Это сумма Z двух случайных величин, которая тоже будет случайной величиной с нормальным распределением, с плотностью вероятности  , с параметрами
, с параметрами 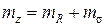 - математическое ожидание и
- математическое ожидание и 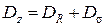 - дисперсия. Для оценки прочности композиция имеет вид
- дисперсия. Для оценки прочности композиция имеет вид  . Тогда
. Тогда  . Плотность вероятности величины Z показана на рис. 5.40, из которого видно, что вероятность безотказной работы равна площади под графиком
. Плотность вероятности величины Z показана на рис. 5.40, из которого видно, что вероятность безотказной работы равна площади под графиком  справа от оси ординат. Вероятность безотказной работы
справа от оси ординат. Вероятность безотказной работы
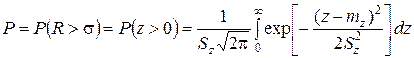 .
.
Произведем замену переменной  ,
,  . На нижнем пределе при
. На нижнем пределе при  (
( ) имеем
) имеем 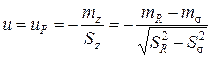 . Здесь
. Здесь  - квантиль, соответствующая вероятности безотказной работы Р. Итак, вероятность безотказной работы станет
- квантиль, соответствующая вероятности безотказной работы Р. Итак, вероятность безотказной работы станет
 . (7)
. (7)
где  - табулированная функция[2],
- табулированная функция[2],  . Можно учесть, что
. Можно учесть, что 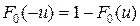 . Если
. Если  , то
, то  . Выражение
. Выражение
 (8)
(8)
называется уравнением связи и служит для определения Р из уравнения
 .
.
Задача 3. Определить вероятность безотказной работы детали, для которой известно 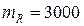 Н,
Н,  Н,
Н,  Н,
Н,  Н.
Н.
Решение. Параметры нормального распределения функции  будут
будут  Н,
Н,  Н. Находим квантиль
Н. Находим квантиль
 . Из таблиц
. Из таблиц  . Итак Р = 0,99.
. Итак Р = 0,99.
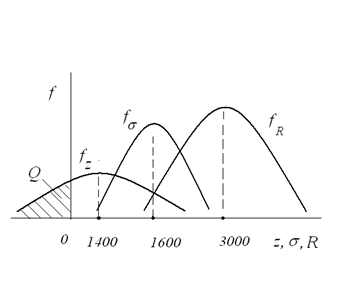
Рис. 5.40. Распределение напряжений, прочности и композиции; заштрихованная площадь Q – вероятность отказа (разрушения)
Задача 4. Даны нормальные распределения: напряжения N (m σ, S σ) = N (246, 28), остаточные напряжения N (-70, 10), прочность N (350,?). Найти среднеквадратичное отклонение прочности S R, обеспечивающее вероятность безотказной работы 0,999.
Решение. Для рабочих и остаточных напряжений используем композицию  МПа,
МПа,  МПа. Из таблиц находим квантиль
МПа. Из таблиц находим квантиль  , поскольку
, поскольку  . Составляем уравнение связи
. Составляем уравнение связи  . Решая это уравнение, находим
. Решая это уравнение, находим  МПа. При таком среднеквадратичном отклонении будет Р = 0,999.
МПа. При таком среднеквадратичном отклонении будет Р = 0,999.
Если функция зависит от нескольких случайных аргументов  , то и функция тоже случайная. Её параметры можно получить методом линеаризации. Для этого функцию представляют в виде ряда Тейлора и первые два члена ряда дают математическое ожидание и дисперсию
, то и функция тоже случайная. Её параметры можно получить методом линеаризации. Для этого функцию представляют в виде ряда Тейлора и первые два члена ряда дают математическое ожидание и дисперсию  ,
,  (здесь все аргументы в производных представлены их математическими ожиданиями). Вообще случайная функция
(здесь все аргументы в производных представлены их математическими ожиданиями). Вообще случайная функция  не следует нормальному закону распределения. Но поскольку получены два параметра распределения, то можно считать, что распределение функции
не следует нормальному закону распределения. Но поскольку получены два параметра распределения, то можно считать, что распределение функции  не очень отличается от нормального. Это позволяет использовать уравнение связи (8).
не очень отличается от нормального. Это позволяет использовать уравнение связи (8).
Задача 5. Коэффициент запаса прочности равен отношению несущей способности к действующей нагрузке  . Имеем случайную функцию двух случайных аргументов. Дано
. Имеем случайную функцию двух случайных аргументов. Дано 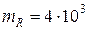 Н,
Н,  Н, коэффициенты вариации
Н, коэффициенты вариации 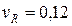 ,
,  . Определить статистические характеристики запаса прочности.
. Определить статистические характеристики запаса прочности.
Решение. Математическое ожидание запаса прочности  . Дисперсия
. Дисперсия  или
или
 . Коэффициент вариации запаса прочности равен
. Коэффициент вариации запаса прочности равен  , почти 20% это многовато.
, почти 20% это многовато.
Задача 6. В трубопроводе обнаружена несквозная поверхностная трещина, расположенная вдоль образующей. Длина трещины на поверхности много больше её глубины. Будем исходить из того, что все параметры задачи имеют нормальное распределение. Исходные данные для расчета: трубная сталь 17Г2С, вязкость разрушения – среднее  МПам0,5, среднеквадратичное отклонение
МПам0,5, среднеквадратичное отклонение  МПам0,5. Давление в трубе
МПам0,5. Давление в трубе  МПа,
МПа,  МПа. Размеры: диаметр трубы
МПа. Размеры: диаметр трубы  м,
м,  м, толщина стенки
м, толщина стенки  м,
м,  м, глубина трещины
м, глубина трещины  м,
м, 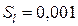 м. Определить вероятность разрушения из-за наличия трещины
м. Определить вероятность разрушения из-за наличия трещины
Решение. Предполагая хрупкое разрушение используем критерий Ирвина  или, составляя композицию, надежность найдем из условия
или, составляя композицию, надежность найдем из условия  . Формулу для коэффициента интенсивности напряжений получим из такого предположения. Мысленно разрежем трубу вдоль образующей напротив трещины и разогнём её до плоскости, касательной к трубе. Получим полосу длиной
. Формулу для коэффициента интенсивности напряжений получим из такого предположения. Мысленно разрежем трубу вдоль образующей напротив трещины и разогнём её до плоскости, касательной к трубе. Получим полосу длиной  , большой ширины, с краевой трещиной глубиной l и растянутой окружным напряжением равным
, большой ширины, с краевой трещиной глубиной l и растянутой окружным напряжением равным
 . В этом случае коэффициент интенсивности напряжений
. В этом случае коэффициент интенсивности напряжений  . Это функция от нескольких случайных аргументов. Среднее значение
. Это функция от нескольких случайных аргументов. Среднее значение  МПам0,5.
МПам0,5.
Дисперсия  или
или
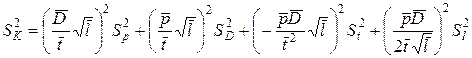 или
или
 МПа2м. Отсюда
МПа2м. Отсюда  МПам0,5.
МПам0,5.
Теперь можно составить уравнение связи
 .
.
С помощью таблиц  . Таким образом, вероятность неразрушения трубы с трещиной равна 0, 976.
. Таким образом, вероятность неразрушения трубы с трещиной равна 0, 976.
.
[1] Это не всегда календарное время, а скорее наработка изделия, выражаемая пробегом, кубометрами и т.п.
[2] Она носит разные названия – интеграл ошибок, функция Лапласа; надо следить за нижним пределом этого интеграла, иногда он равен нулю.

 . Желательно, чтобы вероятность безотказной работы была близка к единице. Она и равна единице, когда деталь или конструкция только что изготовлены. Но в эксплуатации, с течением времени, из-за многих, скрытых от нас факторов, возможность нарушения прочности нарастает, и вероятность безотказной работы падает. При этом вероятность отказа со временем t увеличивается так, что в каждый момент времени
. Желательно, чтобы вероятность безотказной работы была близка к единице. Она и равна единице, когда деталь или конструкция только что изготовлены. Но в эксплуатации, с течением времени, из-за многих, скрытых от нас факторов, возможность нарушения прочности нарастает, и вероятность безотказной работы падает. При этом вероятность отказа со временем t увеличивается так, что в каждый момент времени  . Прочность конструкции (детали) с определенной вероятностью сохраняется при условии, что
. Прочность конструкции (детали) с определенной вероятностью сохраняется при условии, что , (1)
, (1) - нижний предел вероятности безотказной работы, это допускаемая вероятность, аналогично допускаемому напряжению в сопротивлении материалов. Часто вместо
- нижний предел вероятности безотказной работы, это допускаемая вероятность, аналогично допускаемому напряжению в сопротивлении материалов. Часто вместо  . Когда через какое-то время вероятность безотказной работы опустится до величины
. Когда через какое-то время вероятность безотказной работы опустится до величины  , то это время и есть ресурс (гамма-процентный ресурс[1]). Эксплуатация конструкции должна быть прекращена (или произведен ремонт для восстановления работоспособного состояния). Гамма-процентный ресурс Т находят как корень уравнения
, то это время и есть ресурс (гамма-процентный ресурс[1]). Эксплуатация конструкции должна быть прекращена (или произведен ремонт для восстановления работоспособного состояния). Гамма-процентный ресурс Т находят как корень уравнения 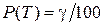 .
. и прочность R характеризуются плотностью распределения их вероятности
и прочность R характеризуются плотностью распределения их вероятности  и
и  . Площадь (заштрихована на рис. 5.37) под кривыми плотностей в области их перекрытия равна вероятности отказа, при котором
. Площадь (заштрихована на рис. 5.37) под кривыми плотностей в области их перекрытия равна вероятности отказа, при котором  . В области
. В области
 в интервал
в интервал  равна
равна  . Вероятность того, что прочность выше напряжения
. Вероятность того, что прочность выше напряжения  . Вероятность того, что одновременно напряжение
. Вероятность того, что одновременно напряжение  (2)
(2)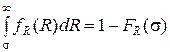
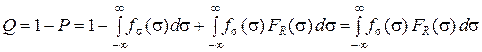 (3)
(3) (4)
(4)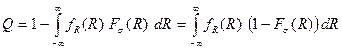 (5)
(5) и
и 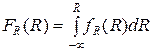 - функции распределения вероятности напряжений и прочности. Записанные формулы предполагают бесконечные «хвосты» у распределений. Если области распределения плотности напряжений и прочности ограничены, то это следует учесть в пределах интегрирования.
- функции распределения вероятности напряжений и прочности. Записанные формулы предполагают бесконечные «хвосты» у распределений. Если области распределения плотности напряжений и прочности ограничены, то это следует учесть в пределах интегрирования. 1/МПа и
1/МПа и  1/МПа. По формуле (2) находим вероятность безотказной работы
1/МПа. По формуле (2) находим вероятность безотказной работы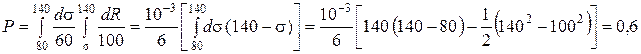
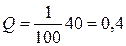 . Результат согласуется с полученной вероятностью Р.
. Результат согласуется с полученной вероятностью Р.
 , причем
, причем 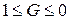 . Остальную часть под интегралом обозначим
. Остальную часть под интегралом обозначим 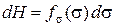 . Тогда
. Тогда  , причем
, причем  . В итоге вероятность безотказной работы примет вид
. В итоге вероятность безотказной работы примет вид . (6)
. (6)

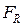
 и
и 

 , показанный на рис. 5.39. Площадь под этим графиком дает вероятность безотказной работы, которая после подсчета оказывается равной Р = 0,76.
, показанный на рис. 5.39. Площадь под этим графиком дает вероятность безотказной работы, которая после подсчета оказывается равной Р = 0,76.
 и прочности с плотностью
и прочности с плотностью  можно использовать их композицию. Это сумма Z двух случайных величин, которая тоже будет случайной величиной с нормальным распределением, с плотностью вероятности
можно использовать их композицию. Это сумма Z двух случайных величин, которая тоже будет случайной величиной с нормальным распределением, с плотностью вероятности  , с параметрами
, с параметрами 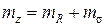 - математическое ожидание и
- математическое ожидание и 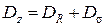 - дисперсия. Для оценки прочности композиция имеет вид
- дисперсия. Для оценки прочности композиция имеет вид  . Тогда
. Тогда  . Плотность вероятности величины Z показана на рис. 5.40, из которого видно, что вероятность безотказной работы равна площади под графиком
. Плотность вероятности величины Z показана на рис. 5.40, из которого видно, что вероятность безотказной работы равна площади под графиком 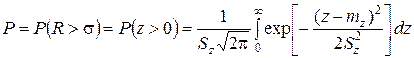 .
. ,
,  . На нижнем пределе при
. На нижнем пределе при  (
( ) имеем
) имеем 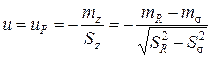 . Здесь
. Здесь  - квантиль, соответствующая вероятности безотказной работы Р. Итак, вероятность безотказной работы станет
- квантиль, соответствующая вероятности безотказной работы Р. Итак, вероятность безотказной работы станет . (7)
. (7) - табулированная функция[2],
- табулированная функция[2],  . Можно учесть, что
. Можно учесть, что 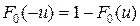 . Если
. Если  , то
, то  . Выражение
. Выражение (8)
(8) .
.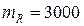 Н,
Н,  Н,
Н,  Н,
Н,  Н.
Н. Н,
Н,  Н. Находим квантиль
Н. Находим квантиль . Из таблиц
. Из таблиц  . Итак Р = 0,99.
. Итак Р = 0,99.
 МПа,
МПа,  МПа. Из таблиц находим квантиль
МПа. Из таблиц находим квантиль  , поскольку
, поскольку  . Составляем уравнение связи
. Составляем уравнение связи  . Решая это уравнение, находим
. Решая это уравнение, находим  МПа. При таком среднеквадратичном отклонении будет Р = 0,999.
МПа. При таком среднеквадратичном отклонении будет Р = 0,999. , то и функция тоже случайная. Её параметры можно получить методом линеаризации. Для этого функцию представляют в виде ряда Тейлора и первые два члена ряда дают математическое ожидание и дисперсию
, то и функция тоже случайная. Её параметры можно получить методом линеаризации. Для этого функцию представляют в виде ряда Тейлора и первые два члена ряда дают математическое ожидание и дисперсию  ,
,  (здесь все аргументы в производных представлены их математическими ожиданиями). Вообще случайная функция
(здесь все аргументы в производных представлены их математическими ожиданиями). Вообще случайная функция  не следует нормальному закону распределения. Но поскольку получены два параметра распределения, то можно считать, что распределение функции
не следует нормальному закону распределения. Но поскольку получены два параметра распределения, то можно считать, что распределение функции  . Имеем случайную функцию двух случайных аргументов. Дано
. Имеем случайную функцию двух случайных аргументов. Дано 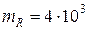 Н,
Н,  Н, коэффициенты вариации
Н, коэффициенты вариации 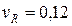 ,
,  . Определить статистические характеристики запаса прочности.
. Определить статистические характеристики запаса прочности. . Дисперсия
. Дисперсия  или
или . Коэффициент вариации запаса прочности равен
. Коэффициент вариации запаса прочности равен  , почти 20% это многовато.
, почти 20% это многовато. МПам0,5, среднеквадратичное отклонение
МПам0,5, среднеквадратичное отклонение  МПам0,5. Давление в трубе
МПам0,5. Давление в трубе  МПа,
МПа,  МПа. Размеры: диаметр трубы
МПа. Размеры: диаметр трубы  м,
м,  м, толщина стенки
м, толщина стенки  м,
м,  м, глубина трещины
м, глубина трещины  м,
м, 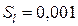 м. Определить вероятность разрушения из-за наличия трещины
м. Определить вероятность разрушения из-за наличия трещины или, составляя композицию, надежность найдем из условия
или, составляя композицию, надежность найдем из условия  . Формулу для коэффициента интенсивности напряжений получим из такого предположения. Мысленно разрежем трубу вдоль образующей напротив трещины и разогнём её до плоскости, касательной к трубе. Получим полосу длиной
. Формулу для коэффициента интенсивности напряжений получим из такого предположения. Мысленно разрежем трубу вдоль образующей напротив трещины и разогнём её до плоскости, касательной к трубе. Получим полосу длиной  , большой ширины, с краевой трещиной глубиной l и растянутой окружным напряжением равным
, большой ширины, с краевой трещиной глубиной l и растянутой окружным напряжением равным . В этом случае коэффициент интенсивности напряжений
. В этом случае коэффициент интенсивности напряжений  . Это функция от нескольких случайных аргументов. Среднее значение
. Это функция от нескольких случайных аргументов. Среднее значение  МПам0,5.
МПам0,5. или
или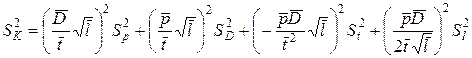 или
или МПа2м. Отсюда
МПа2м. Отсюда  МПам0,5.
МПам0,5. .
. . Таким образом, вероятность неразрушения трубы с трещиной равна 0, 976.
. Таким образом, вероятность неразрушения трубы с трещиной равна 0, 976.


