Методи встановлення зв’язку
Оскільки у педагогічному процесі більшість явищ взаємообумовлені і взаємопов’язані, то дослідникам часто доводиться встановлювати наявність або відсутність зв’язку між досліджуваними параметрами, використовуючи коефіцієнти кореляції. Метод кореляції допомагає з високою ймовірністю стверджувати наявність зв'язку між параметрами. Зокрема, можна встановити залежність успішності учнів із навчального предмету від розвитку їхньої пізнавальної активності, спостережливості або загальнонавчальних умінь. Для інтервальних шкал застосовують лінійну кореляцію (за К. Пірсоном), а для порядкових і невеликих вибірок – порядкову, або рангову кореляцію (за Спірменом). Лінійна кореляція (за К.Пірсоном) Обчислюється коефіцієнт лінійної кореляції (ρ) за формулою:
де (хi – (yi – По-іншому ця формулу можна представити так:
Отриманий емпіричний коефіцієнт лінійної кореляції (remp) слід порівняти з його табличним значенням (rkrit) (див. табл. 3.13), у якій подані 95% і 99 % ймовірності та n – кількість пар, що порівнюються.
Таблиця 3.13 Таблиця достовірності коефіцієнта лінійної кореляції
Якщо ׀remp׀ ≥ rkrit, то існує зв’язок між двома досліджуваними явищами. Причому чим більша різниця між remp і rkrit, тим сильнішим цей зв’язок. Якщо remp має знак "–", то зв’язок між явищами, що досліджуються є оберненим, якщо remp "+" – зв’язок прямий. Коли ׀remp׀ < rkrit, то лінійний зв’язок між двома досліджуваними параметрами відсутній.
|

 (Формула 3.10)
(Формула 3.10)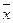 ) – відхилення кожного окремого значення х від середнього арифметичного (
) – відхилення кожного окремого значення х від середнього арифметичного (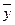 ) − відхилення кожного окремого значення y від середнього арифметичного (
) − відхилення кожного окремого значення y від середнього арифметичного (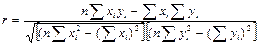 (Формула 3.11)
(Формула 3.11)


