Міри центральної тенденції
Для характеристики і короткого опису результатів дослідження в статистиці широко використовуються міри центральної тенденції результатів дослідження (найбільш типові значення змінної): середнє арифметичне (математичне очікування), мода, медіана. 1. Зважене середнє арифметичне (
де:
N – кількість членів сукупності. Якщо значення елементів сукупності не повторюються, тобто виявляються лише один раз (f=1), то у такому випадку можна користуватись формулою простого арифметичного середнього:
Наприклад, обчислимо середнє арифметичне для такого варіаційного ряду значень: 3, 4, 4, 6, 7, 7, 7, 7, 9, 9, 10.
Підрахунок середнього арифметичного досить простий. Але є свої особливості в його практичному застосуванні. Наведемо приклад. Учні 2-х класів виконували тестові завдання з математики. У класі "А" – 10 учнів, вони в середньому виконали по 4 тестових завдання. У класі "Б" − 20 учнів, середнє арифметичне цього класу – 8 завдань. Необхідно обчислити середнє арифметичне для обох класів.
А n1 = 10, Б n2 = 20, Відразу ж виникає бажання додати середні арифметичні й поділити на два, що більшість і робить. Але це дасть неправильний результат, адже не враховується кількість учнів у класах. Для підрахунку використовується формула:
2. Медіана (Ме) – це центральне значення ряду, тобто значення середнього члена впорядкованого ряду значень. Медіану можна використовувати для значень, що вимірювались за допомогою інтервальних і порядкових шкал. Для обчислення медіани (Ме) певного ряду, перш за все, його слід упорядкувати, тобто розташувати значення в порядку зростання або зменшення значень. Порядковий номер медіани (i) у такому ряді обчислюється за формулою:
(Формула 3.4),
де N – кількість членів ряду. Якщо N – непарне число, тобто у варіаційному ряді непарна кількість членів, то медіаною буде значення середнього члена ряду. Наприклад, у ряді 1, 2, 5, 8, 10, 31, 35 медіаною (Ме) буде число 8. Якщо N – парне число, тобто у варіаційному ряді парна кількість членів, то у його середині знаходяться два значення. У такому випадку для інтервальних шкал необхідно обчислити одну величину медіани. Нею буде просте середнє арифметичне двох сусідніх середніх членів. Наприклад, для ряду 1, 2, 5, 8, 9, 10, 31, 35 медіаною (Ме) буде число 8,5. 3. Мода (Мо) – це значення, що найчастіше зустрічається у даному варіаційному ряді значень. Вона використовується для характеристики сукупності на основі найпоширенішого явища, наприклад: найпоширеніша оцінка з предмету в класі, найпоширеніша кількість відповідей на тестуванні, найпоширеніша національність учнів класу. Моду можна знаходити для всіх шкал без винятку. Модою буде те значення ряду, що має найбільшу частоту (f). Наприклад, для такого ряду шкільних оцінок 3, 4, 5, 6, 7, 7, 8, 9 модою буде число 7, а для ряду 3, 4, 5, 6, 8, 7, 5, 7, 4, 4, 9, 8, 7, 8, 9 модами будуть 4 і 7. Отже, у ряді може бути декілька мод.
|

 ) можна використовувати для характеристики сукупностей (груп учнів, класів), значення яких вимірювались за інтервальною шкалою. Воно показує загальний рівень будь-якої сукупності і залежить не тільки від індивідуальних значень, але і від їхньої частоти (повторюваності). Середнє арифметичне (
) можна використовувати для характеристики сукупностей (груп учнів, класів), значення яких вимірювались за інтервальною шкалою. Воно показує загальний рівень будь-якої сукупності і залежить не тільки від індивідуальних значень, але і від їхньої частоти (повторюваності). Середнє арифметичне ( (Формула 3.1),
(Формула 3.1), – значення окремих елементів сукупності;
– значення окремих елементів сукупності; – частота вияву окремого значення;
– частота вияву окремого значення; (Формула 3.2)
(Формула 3.2)
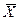 1 = 4
1 = 4 (Формула 3.3)
(Формула 3.3)




