Обчислення дисперсії для 7-Б кл.
 Кількість правильно виконаних
завдань із математики, хі Кількість правильно виконаних
завдань із математики, хі
| Частота оцінок, f
| хі – 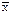
| (хі – 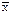 )2 )2
| f· (хі – 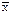 )2 )2
| |
|
| -2,69
| 7,24
| 7,24
| |
|
| -1,69
| 2,86
| 11,44
| |
|
| -0,69
| 0,48
| 2,40
| |
|
| 0,31
| 0,10
| 0,90
| |
|
| 1,31
| 1,72
| 12,04
| |
|
| 2,31
| 5,34
| 10,68
| |
|
| 3,31
| 11,00
| 11,00
| | N = 29
|  = 7,69 = 7,69
| Σ = 55,7
| | σ22 = 1,92
|

Потім знаходимо у F-таблиці (табл. 3.8) значення Fkrit. У таблиці шукаємо значення сукупності з більшою (σ12) та з меншою дисперсією (σ22). Якщо Femp > Fkrit, то вибірки суттєво різняться, якщо Femp ≤ Fkrit, то вибірки схожі за даною ознакою.
У нашому прикладі Femp < Fkrit (1,65 < 1,70), отже, 7-А і 7-Б класи істотно не відрізняються за результатами своїми знаннями з математики. Вірогідність того, що ці класи подібні, складає 95%.
Таблиця 3.8
Таблиця для визначення достовірності F-критерію (достовірність 95%)
| Знаменник
N2 – 1
| Чисельник N1 – 1
| |
|
|
|
|
| ∞
| |
| 6,4
| 6,3
| 6,2
| 5,9
| 5,8
| 5,6
| |
| 5,2
| 5,1
| 5,0
| 4,7
| 4,5
| 4,4
| |
| 4,5
| 4,4
| 4,3
| 4,0
| 3,8
| 3,7
| |
| 4,1
| 4,0
| 3,9
| 3,6
| 3,4
| 3,2
| |
|
| |
| 3,8
| 3,7
| 3,6
| 3,3
| 3,1
| 2,9
| |
| 3,6
| 3,5
| 3,4
| 3,1
| 2,9
| 2,7
| |
| 3,5
| 3,3
| 3,2
| 2,9
| 2,7
| 2,5
| |
| 3,4
| 3,2
| 3,1
| 2,8
| 2,6
| 2,4
| |
|
| |
| 3,3
| 3,1
| 3,0
| 2,7
| 2,5
| 2,3
| |
| 3,2
| 3,0
| 2,9
| 2,6
| 2,4
| 2,2
| |
| 3,1
| 3,0
| 2,9
| 2,5
| 2,3
| 2,1
| |
| 3,1
| 2,9
| 2,8
| 2,5
| 2,3
| 2,1
| |
|
| |
| 3,0
| 2,9
| 2,7
| 2,4
| 2,2
| 2,0
| |
| 3,0
| 2,8
| 2,7
| 2,4
| 2,2
| 2,0
| |
| 2,9
| 2,8
| 2,7
| 2,3
| 2,1
| 1,9
| |
| 2,9
| 2,7
| 2,6
| 2,3
| 2,1
| 1,9
| |
|
| |
| 2,9
| 2,7
| 2,6
| 2,3
| 2,1
| 1,8
| |
| 2,8
| 2,7
| 2,6
| 2,2
| 2,0
| 1,8
| |
| 2,8
| 2,6
| 2,5
| 2,2
| 2,0
| 1,7
| |
| 2,7
| 2,6
| 2,5
| 2,2
| 2,0
| 1,7
| |
|
| |
| 2,7
| 2,6
| 2,4
| 2,1
| 1,9
| 1,7
| |
| 2,7
| 2,5
| 2,4
| 2,1
| 1,9
| 1,6
| |
| 2,6
| 2,5
| 2,3
| 2,0
| 1,8
| 1,5
| |
| 2,5
| 2,4
| 2,3
| 1,9
| 1,7
| 1,4
| |
|
| |
| 2,5
| 2,3
| 2,2
| 1,8
| 1,6
| 1,3
| | ∞
| 2,4
| 2,2
| 2,1
| 1,8
| 1,5
| 1,0
|
N1 – кількість членів І сукупності.
N2 – кількість членів ІІ сукупності.
Якщо Femp > Fkrit, то для більш точної перевірки і встановлення достовірності різниці класів використовується t-критерій, що обчислюється за формулою:
 (Формула 3.8) (Формула 3.8)
 де – середнє арифметичне першої сукупності; де – середнє арифметичне першої сукупності;
– середнє арифметичне другої сукупності;
N1 – обсяг першої вибірки (кількість членів першої сукупності);
N2 – обсяг другої вибірки (кількість членів другої сукупності);
σ12 – дисперсія першої сукупності;
σ22 – дисперсія другої сукупності.
temp порівнюють з tkrit, поданим у таблиці 3.9.
Таблиця 3.9
Таблиця для визначення достовірності t – критерію
| N 1 + N 2 – 2
| Достовірність
| | 95%
| 99%
| |
| 12,71
| 63,66
| |
| 4,30
| 9,93
| |
| 3,19
| 5,84
| |
| 2,78
| 4,60
| |
| 2,57
| 4,03
| |
| 2,30
| 3,36
| |
| 2,23
| 3,17
| |
| 2,18
| 3,06
| |
| 2,15
| 2,98
| |
| 2,12
| 2,92
| |
| 2,10
| 2,88
| |
| 2,09
| 2,85
| |
| 2,07
| 2,82
| |
| 2,06
| 2,80
| |
| 2,05
| 2,78
| |
| 2,05
| 2,76
| |
| 2,04
| 2,75
| |
| 2,02
| 2,70
| |
| 2,00
| 2,66
| |
| 1,98
| 2,62
| | ∞
| 1,96
| 2,58
| N1 – кількість членів І сукупності.
N2 – кількість членів ІІ сукупності.
Якщо temp > tkrit, то сукупності різняться за досліджуваною ознакою, вони не однакові (з 95% ймовірністю), якщо temp ≤ tkrit, то відмінностей немає, досліджувані групи подібні за певною ознакою і можуть бути використані для подальшого експерименту у ролі контрольних та експериментальних груп.

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|
Тема: Составление цепи питания Цель: расширить знания о биотических факторах среды. Оборудование:гербарные растения...
В эволюции растений и животных. Цель: выявить ароморфозы и идиоадаптации у растений Цель: выявить ароморфозы и идиоадаптации у растений. Оборудование: гербарные растения, чучела хордовых (рыб, земноводных, птиц, пресмыкающихся, млекопитающих), коллекции насекомых, влажные препараты паразитических червей, мох, хвощ, папоротник...
Типовые примеры и методы их решения. Пример 2.5.1. На вклад начисляются сложные проценты: а) ежегодно; б) ежеквартально; в) ежемесячно Пример 2.5.1. На вклад начисляются сложные проценты: а) ежегодно; б) ежеквартально; в) ежемесячно. Какова должна быть годовая номинальная процентная ставка...
|
Факторы, влияющие на степень электролитической диссоциации Степень диссоциации зависит от природы электролита и растворителя, концентрации раствора, температуры, присутствия одноименного иона и других факторов...
Йодометрия. Характеристика метода Метод йодометрии основан на ОВ-реакциях, связанных с превращением I2 в ионы I- и обратно...
Броматометрия и бромометрия Броматометрический метод основан на окислении восстановителей броматом калия в кислой среде...
|
|

 Кількість правильно виконаних
завдань із математики, хі
Кількість правильно виконаних
завдань із математики, хі
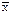
 = 7,69
= 7,69

 (Формула 3.8)
(Формула 3.8) де – середнє арифметичне першої сукупності;
де – середнє арифметичне першої сукупності;


