СТАТИСТИЧЕСКОЕ ПРИЛОЖЕНИЕ: ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
Для того чтобы при наличии двух независимых переменных проверить статистическую значимость двух результатов действия независимой переменной, а также взаимодействие между переменными, применяется F-критерий. Принципы его применения точно такие же, как и описанные в предыдущем приложении. Для того чтобы выявить, достаточно ли величина отношения превышает 1, чтобы отвергнуть нуль-гипотезу, производится сравнение межгрупповой оценки дисперсии генеральной совокупности с внутригрупповой оценкой.
Как получить внутригрупповую оценку, уже было показано. Межгрупповая оценка определяется раздельно для каждого из двух основных результатов действия и для взаимодействия. Таким образом, вычисляются три величины F; каждая полученная величина сравнивается с табличным значением критерия для альфа-уровня, равного 0,05 или 0,01. Это значение критерия можно найти в статистической таблице 3.
Эксперимент с двумя независимыми переменными
Давайте по-другому рассмотрим четыре выборки наших данных по времени реакции. Допустим, что на самом деле эксперимент на время реакции проводился с двумя независимыми переменными: одной из них был тип стимула – свет или тон, другой – тип реакции: простая реакция или реакция выбора. Простая реакция означает нажатие левой кнопки, когда сигнал появляется слева, нажатие правой – когда он появляется справа. Вернемся к исходным обозначениям: условие А представляет простую реакцию на световой стимул; условие Б – простую реакцию на тон; условие В – реакцию выбора на свет; Τ – реакцию выбора на тон. Опыт проводился на четырех группах по 17 испытуемых. Ниже приводятся средние времена реакций, полученные для четырех групп испытуемых.
Различие, связанное с ответом (типом реакции), представлено в этом случае различием между строками, а различия, – вызванные стимулом, представлены различиями между столбцами. Таким образом, произведение реакции на стимул есть произведение строки на столбец (стр×стл). В матрице г строк и с столбцов, в нашем случае r=с=2. Внутригрупповое среднее квадратичное
Для тех же четырех групп данных можно использовать предыдущие расчеты для вычисления среднего квадратичного внутри группы (СКВВГ):
Или
СКВГ = 4306 + 5808 + 5391 + 4673 = 20178.
Как вы заметили, индексы у слагаемых уже новые. ∑х2r1c1 означает, что (полученная внутри группы величина х2 соответствует строке 1 (простая) и столбцу 1 (тон). Точно так же ∑х2r2c2 означает величину для строки 2 (выбор) и столбца 2 (свет) и т. д.
Здесь для нахождения среднего квадратичного можно снова применить формулу (7.6) (поскольку r×с = k):
Из того, что 68 испытуемых делятся на 4 группы, как и ранее, следует
Среднее квадратичное по строкам
Вначале найдем сумму квадратов по строкам и из нее найдем среднее квадратичное по строкам. Разности между средним по каждой строке и общим средним вычисляются следующим образом:
dr1 = Mr1 – Мобщ, dr2 = Mr2 – Мобщ (8.2)
или:
dr1 = 173,5 – 215,5 = –42,0, dr2 = 257,5 – 215,5= +42,0.
Сумма квадратов по строкам – это сумма квадратов этих d-значений, умноженная на произведение числа случаев в группе η и числа столбцов с:
СКстр = пc(d2r1+ d2r2) и т. д., если есть последующие строки. (8.3)
Здесь
СКВстр = 172(1764,0 + 176,40) = 119952
Число степеней свободы для строк равно их числу минус 1:
dfстр = r – 1. (8.4)
В нашем случае
dfстр = 2 – 1 = 1.
И здесь также межгрупповое среднее квадратичное находится делением суммы квадратов на число степеней свободы. Поэтому для строк
или:
Среднее квадратичное по столбцам
Совершенно аналогичные процедуры могут быть сделаны и относительно столбцов. Вначале
dc1 = Mc1 – Mобщ, dc2 = Mc2 – Mобщ (8.6)
или:
dc1 = 206,0 – 215,5 = –9,5, dc2 = 225,0 – 215,5 = +9,5,
СКстл = пr(d2c1+ d2c2) и т. д., если есть еще столбцы (8.7)
или:
СКстл = 17 ∙ 2(90,25 + 90,25) = 6137,
dfстл=с – 1 (8.8)
или:
dfстл = 2 – 1 = 1,
В нашем случае
Среднее квадратичное (строки × столбцы)
Для того чтобы найти сумму квадратов (СКстр×стл), вы должны вначале найти разность между средним каждой подгруппы и общим средним, Затем сложить квадраты этих разностей и умножить полученную сумму на число случаев в группе. Наконец, вычесть из этого числа сумму квадратов по строкам и сумму квадратов по столбцам. Давайте теперь проделаем эти операции шаг за шагом:
dr1c1 = Mr1c1 – Mобщ, dr1c2 = Mr1c2 – Mобщ,
dr2c1 = Mr2c1 – Mобщ, dr2c2 = Mr2c2 – Mобщ.
В нашем случае
dr1c1 = 162,0 – 215,5 = – 53,5,
dr1c2 = 185,0 – 215,5= – 30,5, dr2c1 = 250,0 – 215,5 = + 34,5,
dr2c2 = 265,0 – 215,5 = + 49,5,
СКстр×стл = n (d2r1c1 + d2r1c2 + d2r2c1 + d2r2c2) – СКстр – СKстл· (8.10)
(Замечание: первая часть уравнения уже вычислялась с использованием уравнения 7.4.)
СКстр×стл = 17(2862,25 + 930,25 + 1190,25 + 2450,25) – 119952 – 6137 = 126361 – 119952 – 6137 = 272.
Прежде чем мы перейдем к последнему шагу вычисления среднего квадратичного (СКВстр×стл), мы должны найти число степеней свободы для взаимодействия строк и столбцов. Вспомним, что мы сравниваем разности по одной независимой переменной, вызванные действием другой независимой переменной. Существуют (r – 1) разностей по строкам и (с – 1) при сравнении этих строк с разностями по столбцам. Таким образом, общее число df равно произведению (r – 1)(с – 1). В нашем случае, где всего две строки и два столбца, взаимодействие (строки×столбцы) равно 1:
dfстр×стл = (r – 1)(с – 1) (8.11)
или:
dfстр×стл = (2 – 1)(2 – 1) = 1.
Среднее квадратичное по строкам и столбцам равно сумме квадратов по строкам и столбцам, деленное на 13соответствующее число степеней свободы:
В нашем случае
Вычисление F-отношения
Теперь у нас есть четыре оценки популяционной дисперсии σ̅2X. Это (1) внутригрупповое среднее квадратичное; (2) среднее квадратичное по строкам; (3) среднее квадратичное но столбцам и (4) среднее квадратичное – строки×столбцы. Мы можем использовать внутригрупповое среднее квадратичное как знаменатель при вычислении F-отношения относительно каждого из остальных средних квадратичных. Введение знаменателя часто называют показателем ошибки, имея в виду несистематическое изменение, которое невозможно контролировать в экспериментальных условиях:
В нашем случае
Таким же образом,
или:
И еще раз соответственно:
или:
Принятие или отвержение нуль-гипотезы
Аналогично тому, как это делалось в статистическом приложении к главе 7, мы воспользуемся Статистической таблицей 3 для нахождения критического Значения F. Для Fстр имеется 1df в числителе и 64df в знаменателе. Табличное значение для отвержения нуль-гипотезы для 1 и 65df равно 7,04 на уровне 0,01, Очевидно, что полученная нами величина 380,80 позволяет на этом уровне отклонить нуль-гипотезу. Для Fстр комбинация в числителе и знаменателе та же самая. И здесь полученная величина 19,48 позволяет отклонить нуль-гипотезу на альфа-уровне, равном 0,01.
Для Fстр×стл мы также ищем табличное значение для 1 и 65df. Полученная нами величина 0,86 не позволяет отклонить нуль-гипотезу даже для альфа-уров-ня = 0,05. Критическое значение здесь равно 3,99. F, меньшее единицы, может быть получено лишь для выборочного распределения. В этом случае оно просто не может быть статистически значимым.
Таблица дисперсионного анализа
Дисперсионный анализ можно подытожить в виде следующей таблицы. Обратите внимание, что степени свободы являются аддитивными так же, как и суммы квадратов.
Дисперсионный анализ. Эксперимент на время реакции с разными типами стимулов и видами реакций
Задача. Используйте данные из задачи в статистическом приложении к главе 7 и проведите дисперсионный анализ с составлением таблицы дисперсионного анализа. Снова данные получены для шести раздельных групп испытуемых. Одной переменной является величина награды, второй переменной – трудность задачи. Данные из главы 7 должны быть использованы следующим образом.
|
(8.5)
(8.9)
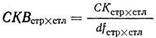(8.12)
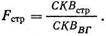(8.13)
(8.14)
(8.15)
