Эвристический (упорядоченный) поиск

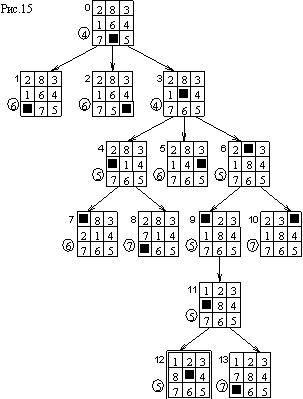
Идея, лежащая в основе большинства эвристических алгоритмов, состоит в том, чтобы оценивать (с помощью численных оценок) перспективность нераскрытых вершин пространства состояний (с точки зрения достижения цели), и выбирать для продолжения поиска наиболее перспективную вершину. Самый обычный способ использования эвристической информации – введение так называемой эвристической оценочной функции. Эта функция определяется на множестве вершин пространства состояний и принимает числовые значения. Значение оценочной функции Est(V) может интерпретироваться как перспективность раскрытия вершины, или вероятность ее расположения на решающем пути. Обычно считают, что меньшее значение Est(V) соответствует более перспективной вершине, и вершины раскрываются в порядке увеличения (возрастания) значения оценочной функции.

Таким образом, основные шаги алгоритма эвристического перебора таковы:

Шаг 1. Поместить начальную вершину в список Open и вычислить ее оценку (значение оценочной функции).

Шаг 2. Если список Open пуст, то окончание алгоритма и выдача сообщения о неудаче поиска, в противном случае перейти к шагу 3.

Шаг 3. Выбрать из списка Open вершину с минимальной оценкой (среди вершин с одинаковой минимальной оценкой выбирается любая); перенести эту вершину (назовем ее Current) в список Closed.

Шаг 4. Если Current – целевая вершина, то окончание алгоритма и выдача решения задачи, получающегося просмотром указателей от нее к начальной вершине, в противном случае перейти к следующему шагу.

Шаг 5. Раскрыть вершину Current, построив все ее дочерние вершины. Если таких вершин нет, то перейти к шагу 2, в ином случае – к шагу 6.

Шаг 6. Для каждой дочерней вершины вычислить оценку (значение оценочной функции), поместить все дочерние вершины в список Open, и построить указатели, ведущие от этих вершин к родительской вершине Current. Перейти к шагу 2.

Заметим, что поиск в глубину можно рассматривать как частный случай упорядоченного поиска с оценочной функцией Est(V) = D(V), а поиск в ширину -- с Est(V) = 1/D(V), где D – глубина вершины V.

Рассмотрим работу алгоритма эвристического поиска опять же на примере игры в восемь. В качестве оценочной функции можно взять следующую:

Est(V) = D(V) + K(V) где

D(V) – глубина вершины V, или число ребер дерева на пути от этой вершины к начальной вершине;

K(V) – число фишек позиции-вершины V, лежащих не на «своем» месте.

На рис.5.6 показано дерево, построенное алгоритмом упорядоченного перебора с указанной оценочной функцией (начальное состояние то же, что и в примерах рис. 5.4 и 5.5, а целевое показано на рис.5.2). Оценка каждой вершины приведена рядом с ней внутри кружка. Отдельно стоящие цифры, как и раньше, показывают порядок, в котором раскрывались вершины. Видно, что так как минимизация оценочной функции производится для всего пространства состояний, то раскрываемые друг за другом вершины могут располагаться в совершенно разных частях пространства состояний.

Рис. 5.6 Упорядоченный перебор с оценочной функцией

Найденный путь решения задачи длиною в пять ходов может быть получен и другими методами перебора, но использование оценочной функции приводит к существенно меньшему числу раскрытий вершин. Действительно, сравнение трех алгоритмов перебора показывает, что

В общем случае (в среднем) алгоритм эвристического поиска обнаруживает решение быстрее алгоритмов слепого перебора. Важно однако, что использование эвристической функции не может гарантировать сокращение поиска во всех случаях, и иногда (хотя и редко) решение задачи может искаться дольше, чем с использованием слепого метода.

Ясно, что подбор «хорошей» эвристической функции (существенно сокращающей поиск) – наиболее трудный момент при формализации задачи, особенно это важно в больших пространствах состояний. Можно сравнивать различные оценочные функции для одной задачи по их эвристической силе, т.е. по тому, насколько они сокращают (убыстряют) поиск.

Граф-пространство состояний для головоломки-игры в восемь достаточно велик (в игре в пятнадцать фишек он на порядок больше), поэтому хотя в принципе применимы алгоритмы слепого поиска, предпочтителен все же эвристический поиск.