Нечеткая логика Заде
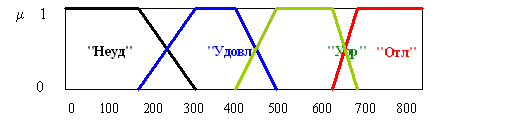
Нечеткая логика (называемая также "логикой возможностей") была придумана Л. Заде, который распространил булеву логику на действительные числа. В булевой алгебре 1 представляет истину, а 0 — ложь. То же имеет место и в нечеткой логике, но, кроме того, используются также все дроби между 0 и 1, чтобы указать на частичную истину. Так, запись р(высокий (Х)) =0,75 говорит о том, что предположение "Х — высокий", в некотором смысле на три четверти истинно. Точно так же оно на одну четверть ложно. Пример. В рейтинговой системе оценки знаний по каждой дисциплине задается некоторая базовая шкала баллов (обычно используется шкала [0,1000]), на которой задаются интервалы, дающие студенту право на получение оценки "отлично", "хорошо", "удовлетворительно", "неудовлетворительно". Фактически эти интервалы выступают как носители нечетких множеств "отлично", "хорошо", "удовлетворительно", "неудовлетворительно", так как за разные баллы из одного и того же интервала преподаватель ставит одну и ту же оценку с разной степенью уверенности. На рисунке приведены графики функций принадлежности оценок, характеризующие степень уверенности некоторого преподавателя в оценке знаний студента по дисциплине в зависимости от величины набранного им по рейтингу балла.
Приведенный пример показывает, что функция принадлежности нечеткого множества (понятия) формируется субъективно и может иметь для одного и того же понятия различный вид у разных субъектов и даже у одного и того же субъекта при различных обстоятельствах и настроениях.
Логические операции над нечеткими высказываниями. Нечеткие высказывания могут быть простыми и составными. Составные высказывания образуются из простых с помощью логических операций, часто называемых в логике также логическими связками из-за их роли в предложениях естественного языка. Так в обычной речи часто употребляются слова не, и, или, и словосочетания если …то…, тогда и только тогда, равносильно, соответствующие основным логическим операциям математической логики. В отличие от традиционной математической логики, в нечеткой логике этим операциям придается специфический смысл. Причем, в зависимости от области применения, этот смысл может быть различным. Например, при изучении случайных явлений целесообразно степени уверенности рассматривать как вероятности и тогда логические операции над нечеткими высказываниями приобретают смысл известных операций над вероятностями случайных событий. Здесь будет рассматриваться интерпретация логических операций над нечеткими высказываниями, предложенная основоположником нечеткой логики Лотфи Заде (Lotfi Zadeh) и применяемая, преимущественно, в тех случаях, когда нечеткость высказываний обусловлена неполнотой информации о предмете суждения. Речь пойдет о так называемой минимаксной логике Заде. Для комбинирования нецелочисленных значений истинности в нечеткой логике определяются эквиваленты операций И, ИЛИ и НЕ (коньюнкция, дизъюнкция, отрицание): pl И р2 = min (р l, р2) (т. е. меньшее), pl ИЛИ р2 = max(pl, р2) (т.е. большее), НЕ pl = 1 — pl (т. е. "обратное значение"). В составных высказываниях порядок выполнения введенных логических операций определяется скобками, а при отсутствии скобок - в следующем порядке:, &, Ú. Таким образом, обрывочные сведения можно комбинировать на основе строгих и согласованных методов, поэтому нечеткая логика с успехом используется, например, в системе обеспечения принятия решений REVEAL. Слабым моментом в применениях нечеткой логики является отображение или функция принадлежности. Предположим, что мне 35, насколько истинно предложение, что я старый? Равна ли эта величина 0,5, поскольку я прожил примерно полжизни? Или что-то вроде 0,4 или 0,6 будет более реалистичным?
|

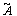 называется нечетким высказыванием, если допускается, что
называется нечетким высказыванием, если допускается, что 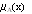 ,
,  , заданной на множестве Х= {"ложь", "истина"}.
, заданной на множестве Х= {"ложь", "истина"}.


