Решение оптимизационных задач с помощью генетических алгоритмов
1. Андрейчиков А.В., Андрейчикова О.Н. Интеллектуальные информационные системы. - М: Финансы и статистика, 2004. 2. Назаров А.В., Лоскутов А.И. Нейросетевые алгоритмы прогнозирования и оптимизации систем – СПб.: Наука и Техника, 2003. – 384 с.: ил. 3. Рутковская Д., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с. польск. И. Д. Рудинского. – М.: Горячая линия – Телеком, 2004.-452 с. 4. Усков А. А. Интеллектуальные технологии управления. Искусственные нейронные сети и нечеткая логика. - М.: Горячая линия-Телеком, 2004.- 143 с.
Лабораторная работа № 4 Решение оптимизационных задач с помощью генетических алгоритмов
Цель работы Целью лабораторной работы является ознакомление с инструментальным средством Mendel, а также приобретение практического опыта использования генетических алгоритмов для решения оптимизационных задач.
1. Краткие теоретические сведения Появление генетических алгоритмов (ГА) можно отнести к концу шестидесятых – началу семидесятых годов, когда они были впервые описаны в работе Дж. Холланда "Адаптация в природе и искусственных системах". Их общий смысл сводится к моделированию процесса эволюции. Как и в природе, задача алгоритма - отбор наиболее пригодных особей для дальнейшего участия в процессе воспроизводства и, таким образом, нахождение наиболее пригодного индивидуума-решения. Методы ГА эффективны при решении задач оптимизации, задач управления сложными динамическими объектами в условиях неопределенности. При описании ГА используются определения заимствованные из генетики: Популяция – конечное множество особей (индивидуумов), каждый индивидуум - эквивалент решения задачи. Особи, входящие в популяцию, в генетических алгоритмах представляются хромосомами с закодированным в них множеством параметров задачи. Хромосомы – упорядоченные последовательности генов. Ген – атомарный элемент хромосомы, в ГА представлен в виде двоичных цифр (единица и нуль). Генотип (структура) – набор хромосом данной особи. Фенотип – набор значений, соответствующих данному генотипу. Аллель – значение конкретного гена. Локус (позиция) – место размещения данного гена в хромосоме. Множество позиций генов - Локи. Функция приспособленности - представляет собой меру приспособленности данной особи в популяции, позволяет оценить степень приспособленности конкретных особей в популяции и выбрать из них наиболее приспособленные (т. е. имеющие наибольшие значения функции приспособленности) в соответствии с эволюционным принципом выживания “сильнейших”. На каждой итерации ГА приспособленность каждой особи данной популяции оценивается при помощи функции приспособленности, и на этой основе создается следующая популяция особей, которая представляет собой множество потенциальных решений задачи. Очередная популяция в ГА называется поколением, а к вновь создаваемой популяции особей применяется термин “новое поколение” или “поколение потомков”. Классический генетический алгоритм состоит из следующих этапов: 1) Инициализация – формирование исходной популяции, заключается в случайном выборе заданного количества хромосом (особей), представляемых в виде последовательности двоичных чисел. 2) Оценка приспособленности хромосом. Заключается в расчете функции приспособленности для каждой хромосомы популяции. 3) Проверка условия остановки алгоритма. Определяются условия завершения выполнения алгоритма. Алгоритм может быть остановлен по истечении определенного времени выполнения, либо после завершения заданного количества итераций. Остановка может произойти также в том случае, если работа алгоритма не приводит к улучшению уже достигнутого результата. 4) Селекция хромосом – заключается в выборе тех хромосом, которые будут участвовать в создании потомков для следующей популяции. Среди методов селекции наиболее популярным является метод Рулетки. Метод Рулетки позволяет отбирать особей с помощью
При таком отборе члены популяции с более высокой приспособленностью будут чаще выбираться, чем особи с низкой приспособленностью. Существуют и другие методы селекции, например, турнирный отбор, элитный отбор и т.д. 5) Применение генетических операторов. Этот этап позволяет сформировать следующую популяцию потомков от уже созданной родительской популяции. Различают два генетических оператора: оператор скрещивания и оператор мутации. Скрещивание осуществляется следующим образом: 1. из родительской популяции случайным способом выбираются хромосомы и объединяются в пары. 2. для каждой отобранной пары разыгрывается позиция гена (локус), т. е. происходит обмен генами между двумя родительскими хромосомами, и в результате получается потомок, хромосома которого на позициях от 1 до Оператор мутации с вероятностью Хромосомы, полученные в результате применения указанных генетических операторов, образуют новую популяцию, и вся предшествующая популяция хромосом заменяется полученной. 6) Выбор наилучшей хромосомы. Лучшей считается хромосома с наилучшим значением функции приспособленности.
2. Описание программы Mendel Программа Mendel предназначена для решения задач оптимизации. Реализует в себе диплоидную версию генетического алгоритма и позволяет работать с произвольными пользовательскими задачами оптимизации. Целевая функция оптимизационной задачи и ее параметры описывается во внешней dll-библиотеке задачи оптимизации. В общем случае для решения задачи с помощью программы Mendel требуется: 1) Создать задачу оптимизации с помощью мастера Новая задача, указав dll-библиотеку задачи. 2) Задать параметры генетического алгоритма (число особей в популяции, критерии останова работы алгоритма, параметры процедур скрещивания, мутации, отбора и т.д.) 3) Запустить работу генетического алгоритма. Информацию о результатах поиска можно сохранить в виде отчета Рассмотрим работу с программой Mendel на следующих примерах: Пример 1. Найти минимум функции
Ниже приведен график тестовой функции для случая двухмерного поискового пространства (рис. 1). Даже этот упрощенный вариант позволяет оценить сложность поставленной задачи минимизации.
Рис. 1. – График функции
Для решения задачи необходимо проделать следующие шаги: 1) Выбрать команду Новая задача пункта меню Задача в главном окне программы и указать путь к библиотеке, хранящей параметры и целевую функцию решаемой задачи (рис. 2).
Рис. 2 – Выбор библиотеки задачи оптимизации
2) Далее зададим количество особей в популяции и способ их формирования (например, случайным образом) (рис. 3).
Рис. 3 – Задание параметров популяции 3) Следующее окно программы (рис. 4) позволяет управлять работой алгоритма и содержит в себе главное меню, панель инструментов, панель Поиск, переключатель показа/скрытия панели Поиск, панель Статистика, переключатель показа/скрытия панели Статистика, строку состояния.
Рис. 4
Главное меню содержит следующие пункты: 1) Меню Задача позволяет создавать и управлять файлами задач и шаблонов задач, содержит следующие команды: Новая задача – запуск мастера создания новой задачи; Новая задача по шаблону – открывает шаблон задачи и запускает мастер Новая задача с параметрами из шаблона; Открыть задачу – открывает задачу или ее резервную копию; Последние задачи – позволяет открыть задачу из списка последних задач; Сохранить задачу - сохраняет текущую задачу; Сохранить задачу как – сохраняет задачу под новым именем; Сохранить как шаблон – сохраняет текущую задачу как шаблон в виде файла с расширением.m4p. 2) Меню Правка позволяет управлять отдельными особями в популяции Добавить особи (Удалить особи) – позволяет редактировать число особей в популяции; Пересчитать популяцию – пересчет приспособленности всех особей популяции. 3) Меню Работа позволяет управлять процессом поиска решения задачи и экспортировать результаты работы Запустить – запуск алгоритма; Остановить – останавливает работу алгоритма; Отчет – создает отчет о процессе поиска и лучшем решении задачи в виде файла с расширением.rep; Выполнить – запускает определенное пользователем приложение; 4) Меню Параметры позволяет произвести общую и точную настройку параметров программы Генетический алгоритм – открывает окно с параметрами алгоритма; Условие окончания – позволяет выбрать критерий останова алгоритма; Меню пользователя – позволяет произвести настройку меню пользователя; Настройка – позволяет задать настройки пользователя.
Панель Поиск содержит закладки: Целевая функция – отображает график изменения величины целевой функции для всех особей в зависимости от порядкового номера эпохи; Область поиска – отображает положение особей популяции текущей эпохи.
Панель Статистика содержит закладки: Задача – отображает сведения о задаче, статистические данные о процессе поиска решения и характеристики популяции; Решение – отображает текущее решение задачи; ГА – отображает статистические данные о работе генетического алгоритма.
Для рассматриваемого нами примера, после запуска алгоритма при следующих параметрах: число особей - 200, останов после достижения 1000 эпохи, были получены следующие результаты (рис. 6).
Рис. 6 – Результат работы генетического алгоритма
Пример 2. Рассмотрим пример создания библиотеки dll для решения пользовательской задачи нахождения минимума функции Напомним, что DLL (Dynamic Link Library) - это один или несколько логически законченных фрагментов кода, сохраненных в файле с расширением.dll. Этот код может быть запущен на выполнение в процессе функционирования какой-либо другой программы, как в случае с программой Mendel (такие приложения называются вызывающими по отношению к библиотеке), но сама dll-библиотека не является исполняемым файлом. Общая структура такой библиотеки реализованной с помощью среды Delphi выглядит следующим образом: library test; varEpoche: longint;RecalcNow: boolean; procedure InitTask(var TaskName: PChar; var MinimizationTask: boolean; var TaskDim: integer; var pMin,pMax,pMap,pEp,pRcN: pointer);beginTaskName:= название задачи;MinimizationTask:= тип задачи минимизации;TaskDim:= размерность задачи;pMin:= указатель на массив нижних пределов области поиска;pMax:= указатель на массив верхних пределов области поиска;pMap:= указатель на массив, описывающий карту хромосомы;pEp:= Addr(Epoche);RecalcNow:= false;pRcN:= Addr(RecalcNow);end; function FitnessFunction(parameters: pointer; var condition: boolean): double;begincondition:= выполнение условия при параметрах parameters;result:= целевая функция от параметров parameters;end;function GetKnownParameters(index: integer; parameters: pointer): boolean;beginparameters:= вектор координат известного решения номер index;result:= было ли присвоено известное значение parameters;end; EXPORTSFitnessFunction,InitTask,GetKnownParameters; BEGINEND.
В данной лабораторной работе будет рассмотрен способ создания dll-библиотеки с помощью среды Lazarus. В самом начале работы необходимо запустить среду Lazarus и выполнить команду Создать меню Файл. В открывшемся окне(рис. 7) необходимо выбрать Library, после чего переходим к редактору исходного кода библиотеки.
Рис. 7 – Создание библиотеки
В редакторе исходного кода запишем: library primer2; type m = double;
const min: m=-500; max: m=500; map: m=16; var Epoche: longint; RecalcNow: boolean;
procedure InitTask(var TaskName: PChar; var MinimizationTask: boolean; var TaskDim: integer; var pMin,pMax,pMap,pEp,pRcN: pointer); begin TaskName:= 'primer2'; MinimizationTask:= true; {true-задача на поиск минимума, false - если поиск максимума} TaskDim:= 1;{размерность задачи} pMin:= addr(min);{указатель на массив нижних пределов области поиска} pMax:= addr(max);{указатель на массив верхних пределов области поиска} pMap:= addr(map);{указатель на массив, описывающий карту хромосомы} pEp:= Addr(Epoche); RecalcNow:= false; {нужно ли пересчитать популяцию} pRcN:= Addr(RecalcNow); end;
function FitnessFunction(parameters: pointer; var condition: boolean): double; var p:^m; begin p:= parameters; condition:= true;{выполнение условия при параметрах parameters} result:= p^*p^-4*p^+3;{целевая функция от параметров parameters} end; function GetKnownParameters(index: integer; parameters: pointer): boolean; var i:integer; p:^m; begin p:=parameters;{вектор координат известного решения номер index} result:=false; if index<=70 then begin p^:=i; result:=true; end; end;
EXPORTS FitnessFunction, InitTask, GetKnownParameters;
BEGIN END. Далее сохраняем проект, и используем созданную нами библиотеку для работы с программой Mendel, как это описано в примере 1.
|

 "запусков" рулетки. Колесо рулетки содержит по одному сектору для каждого члена популяции. В целом вся окружность колеса рулетки соответствует интервалу [0, 100]. Каждой хромосоме, обозначаемой
"запусков" рулетки. Колесо рулетки содержит по одному сектору для каждого члена популяции. В целом вся окружность колеса рулетки соответствует интервалу [0, 100]. Каждой хромосоме, обозначаемой  для i=1,2,…, N (где N обозначает численность популяции) соответствует сектор колеса
для i=1,2,…, N (где N обозначает численность популяции) соответствует сектор колеса  , выраженный в процентах согласно формулам (4.1) и (4.2)
, выраженный в процентах согласно формулам (4.1) и (4.2) (4.1)
(4.1) (4.2)
(4.2) состоит из генов первого родителя, а на позициях от
состоит из генов первого родителя, а на позициях от  до
до 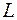 - из генов второго родителя или же потомок, хромосома которого на позициях от 1 до
- из генов второго родителя или же потомок, хромосома которого на позициях от 1 до  изменяет значение гена на противоположное (с 0 на 1 или обратно на позиции m).
изменяет значение гена на противоположное (с 0 на 1 или обратно на позиции m). .
.




 .
.



