Особенности учебно-тренировочной работы с юными спортсменами
Здесь fun - имя функции, xi - входные аргументы функции (их m штук), yi - выходные аргументы функции (их n штук).
Пример. Вычисление факториала. function [x]=fact(k) k=int(k) if k<1 then k=1, end x=1; for j=1:k,x=x*j;end endfunction Наберем этот текст в любом текстовом редакторе и сохраним его в файле с именем fact.sci. Расширение *.sci является для Sclab "родным", но не обязательным. Затем следует вызвать эти файлы из Scilab c помощью команд getf(filename) или exec(filename,-1); Те же операции можно произвести с помощью команд меню File-getf или File-exec. До вызова функции желательно проверить, не была ли уже загружена такая функция ранее. Для этого: exists('fact') Результат: ans = 0. После загрузки файла -->exec('C:\fact'); набираем -->x=fact(5) x = 120 Пример: function z=fun(x, y) // Определение функции z=x.^2 + y.^2; endfunction Сохраним эту функцию под именем fun.sci. После загрузки функции в Scilab мы можем обратиться к ней: -->fun(1,2) ans = 5. Пример. Даны два массива X и Y. Вывести в командное окно имя массива, содержащего наибольшее число элементов, кратных числу три. Решение. Составим программу и сохраним ее под именем t.sci в каталоге C:\DOCUME~1\user\. function g=t(v) s=0; n=length(v); for i=1:n if modulo(v(i), 3)==0 then s=s+1; end end g=s; endfunction Далее сохраним в корневом каталоге C:\ под именем tot, а затем выполним программу x=[1 2 3 5 7 6 12]; y=[5 7 24 15]; d1=t(x), d2=t(y) if d1>d2 then disp('x') elseif d1==d2 then disp('в обоих массивах это число одинаково') else disp('y') end Получим ответ: d1 = 3. d2 = 2. x Запуск файла на выполнение осуществляется так: -->scipad('C:\DOCUME~1\user\t.sci'); -->scipad('C:\tot'); -->exec('C:\tot'); Файл-функция был сохранен в 'C:\DOCUME~1\user\t.sci', файл-сценарий – в 'C:\tot' Это эквивалентно выполнению следующих операций: запускаем Scilab. Далее: открываем файл-функцию File/Open… Далее Execute/Load into Scilab; Открываем файл-сценарий (выполняемый файл) File/Open…Далее File/Exec … Открываются файлы в окне Scilab. Если выходных параметров несколько, то их надо указать в квадратных скобках после слова function. function [var1, var2, …] = fname(список_параметров) // Основной комментарий // Дополнительный комментарий Тело файла с любыми выражениями var1=выражение var2=выражение … endfunction
Пример. Задан вектор
Решение. Набираем и сохраняем в редакторе под именем statv.sci файл function [ mean, stdev ] = statv (x) n=length (x); mean=sum (x) /n; stdev=sqrt (sum ((x-mean).^2) /n); endfunction Далее в командном окне набираем --> v=[1, 2, 3, 4, 5]; --> [a, m]=statv(v) В строках вывода получаем: m = 1.4142136 a = 3. --> Краткий комментарий к программе. Во второй строке файла statv.sci вычисляется количество элементов в массиве x; sum(x) – суммируются все элементы массива x; mean – вычисляется Для создания временной задержки выполнения программы служит команда xpause, которая приостанавливает текущий процесс на число микросекунд, указанных в скобках · хpause(microsecs)
Пример: xbasc(); xset("color",12); xstring(1,1,"Blue"); xpause(5.e6); // временная задержка на 5 секунд xbasc(); xset("color",5); xstring(0,1,"Red");
В результате мы видим в графическом окне вначале надпись "Blue", а затем она исчезает и мы видим сдвинутую по горизонтали надпись "Red". Некоторые полезные функции Scilab для вычисления целой части числа: int(1.9999)=1=int(1.1) int(-1.9999)=-1 int(-0.00001)=0 floor(1.5)=1=floor(1.9)=floor(1.1) floor(-1.1)=-2=floor(-1.8) ceil(1.1)=ceil(1.9)=2 ceil(-1.9)=-1=ceil(-1.2) fix(-1.2)=-1=fix(-1.7) fix(1.7)=1=fix(1.2)
Особенности учебно-тренировочной работы с юными спортсменами Спортивная подготовка школьников решает задачи социокультурного развития и всестороннего воспитания, обеспечивает адаптацию ко все более усложняющимся промышленным технологиям и все более возрастающей напряженности повседневной жизни. Тренировка юных спортсменов представляет собой относительно самостоятельный раздел теории и методики спортивной тренировки – так называемый детский и школьный спорт. Это обусловлено объективными закономерностями, такими как: · Возрастное развитие детского организма проходит интенсивно, но в то же время и неравномерно для отдельных функциональных систем, что в отдельные моменты приводит к кратковременной дисгармонии в деятельности организма и к возникновению критических периодов, которые следует учитывать в процессе спортивных занятий. Это значит, что неверная дозировка тренировочных и особенно соревновательных нагрузок может стать причиной нарушений нормального хода возрастного развития и задержек в росте спортивного мастерства. В то же время знание наиболее благоприятных периодов для развития тех или иных качеств позволяет добиваться наиболее существенных сдвигов в темпах возрастного развития. · Практика и научные исследования показывают, что достижению высокого спортивного мастерства предшествует планомерная учебно-тренировочная работа на протяжении 8-10 лет. К этому времени, то есть к 18-20 годам, функциональная деятельность организма приобретает высокую степень совершенства, что позволяет показывать высокие спортивные результаты. В связи с этим необходимо организовывать знакомство и обучение детей дошкольного и младшего школьного возраста основам спортивно-игровой деятельности. · Научно доказано, что возраст 4-6 лет благоприятен для начального обучения спортивным играм. Такое раннее знакомство детей с играми целесообразно с учетом характерного для нашего времени ускорения темпов умственного и физического созревания, происходящего под влиянием современного научно-технического прогресса, интенсификации информационного потока и улучшения материальных условий жизни. Раннее обучение и последующая спортивная специализация осуществляются через детские спортивные школы, секции коллективов физкультуры, спортивные клубы и коммерческие организации.
|

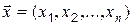 . Вычислить
. Вычислить  и
и .
. ; stdev – вычисляется
; stdev – вычисляется  . В итоге получаем среднее значение
. В итоге получаем среднее значение 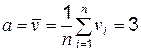 ,
,  .
.


