Задание 5. Имеем следующую задачу (задачу Коши): решить дифференциальное уравнение при начальном условии: .
Имеем следующую задачу (задачу Коши): решить дифференциальное уравнение Решение задачи с помощью ИС Scilab: Применим для решения задачи Коши функцию z=ode(y0,x0,x,f), в качестве параметров которой будем использовать следующие: f - предварительно созданная функция f(x, y) (f(x,y)=y/x+8/x^2 – правая часть нашего дифференциального уравнения); x - координаты сетки; y0, x0 - начальное условие: y (11.6)= 2 (y0 =2, x0 =11.6); z - результат работы функции. Откроем новое окно редактора системы Scilab командой Editor и наберем в нем следующие строки: clc xbasc() function w=f(x,y),w=y/x+(8)./x.^2,endfunction; x0=11.6;y0=2;x=11.6:.2:12.2; z=ode(y0,x0,x,f); [x;z] Задание 6 y =0.4 x 4–6 x 3+6 x 2– x +2 Найти минимум функции.
Так как у целевой функции может быть несколько экстремумов, сначала надо найти отрезок, на котором у нее только одна точка минимума. Это можно сделать, например, с помощью ИС Eureka (Scilab), табулируя целевую функцию или строя ее график. В нашем случае точка минимума x * функции y =0.4 x 4–6 x 3+6 x 2– x +2 лежит на отрезке [ a, b ] = [9, 11]. Решение задачи с помощью ИС Scilab: Откроем окно редактора системы Scilab командой scipad(); и наберем в нем следующие строки: clc function y=gg(x) y=0.4*x.^4-6*x.^3+6*x.^2-x+2; endfunction function [f,g,r]=z(x,r) f=gg(x) g=numdiff(gg,x) endfunction x0=1; [fmin,xmin]=optim(z,x0) Запустив набранный файл на выполнение (Execute/Load into Scilab),в командном окне получим результат xmin = 10.544339 fmin = - 1430.8873 Примечание: Для нахождения наибольшего значения функции y на некотором отрезке [a, b] в ИС Scilab функцию optim применять к функции – y.
|

 при начальном условии:
при начальном условии: 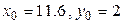 .
.


