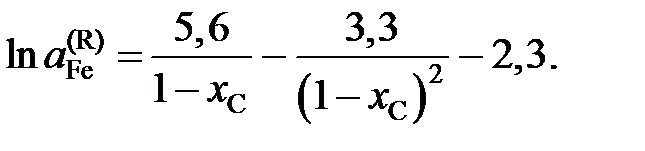Это дает возможность для пересчета активностей при переходе от одного стандартного состояния к другому.
1) осмотр лечащим врачом 2) консультация заведующего отделением 3) осмотр заместителем главного врача по ЭВН 4) представление на ВК МО 5) консилиум с привлечением доктора медицинских наук 58. Укажите вид обследования, проведенного в амбулаторных условиях, при котором может быть выдан листок нетрудоспособности трудоспособному рабочему или служащему на период этого обследования: 1) колоноскопия 2) дуоденальное зондирование 3) рентгеноскопия грудной клетки 4) подбор контактных линз 5) ЭХО-КГ
Это дает возможность для пересчета активностей при переходе от одного стандартного состояния к другому. Для количественной оценки отклонений свойств реального раствора от совершенного и идеального вводится понятие коэффициента активности
Из уравнений (II.29) и (II.30) следует
Например, для бинарного раствора
и является сложной функцией состава. Следовательно, и отношения коэффициентов активностей (II.32) и (II.33) величины не постоянные, зависящие от состава раствора. Для некоторых растворов, например расплавов Fe – Mn, Co – Ni (атомные массы железа и марганца 55,847 и 54,938 г/моль, соответственно; кобальта и никеля – 58,933 и 58,70 г/моль), можно без заметной ошибки считать х 1 М 1 >> х 2 М 2 (х 1» 1),
и соотношение коэффициентов активностей (II.32) и (II.33) является величиной постоянной, но все-таки не равной отношению активностей. В металлургии при описании термодинамических свойств металлических сплавов с ограниченной растворимостью часто за стандартное состояние растворенного вещества используется насыщенный им раствор. 8.1. Определение активностей компонентов бинарного раствора Вычисления выполняются с использованием уравнений (II.25) – (II.34). Пример 2.51. Экспериментально определенные давления насыщенного пара магния над расплавами Mg – Pb разного состава при 1000 K приведены в таблице 2.8. Вычислить активности и коэффициенты активности магния. Таблица 2.8 Результаты экспериментов и вычислений
Решение. Имеющиеся экспериментальные данные позволяют сразу вычислить лишь активности и коэффициенты активности магния по Раулю
причем Отсутствие экспериментальных данных для разбавленных растворов магния в свинце исключает возможность надежного определения активности магния относительно стандартных состояний «гипотетический чистый магний» и «1%-ный идеальный разбавленный раствор». Пример 2.52. Упругости паров серы над растворами серы в жидком железе при 1976 K представлены в таблице 2.9. Рассчитать активности и коэффициенты активности серы. Таблица 2.9 Экспериментальные данные и результаты вычислений активностей и коэффициентов активности серы, Т = 1976 K
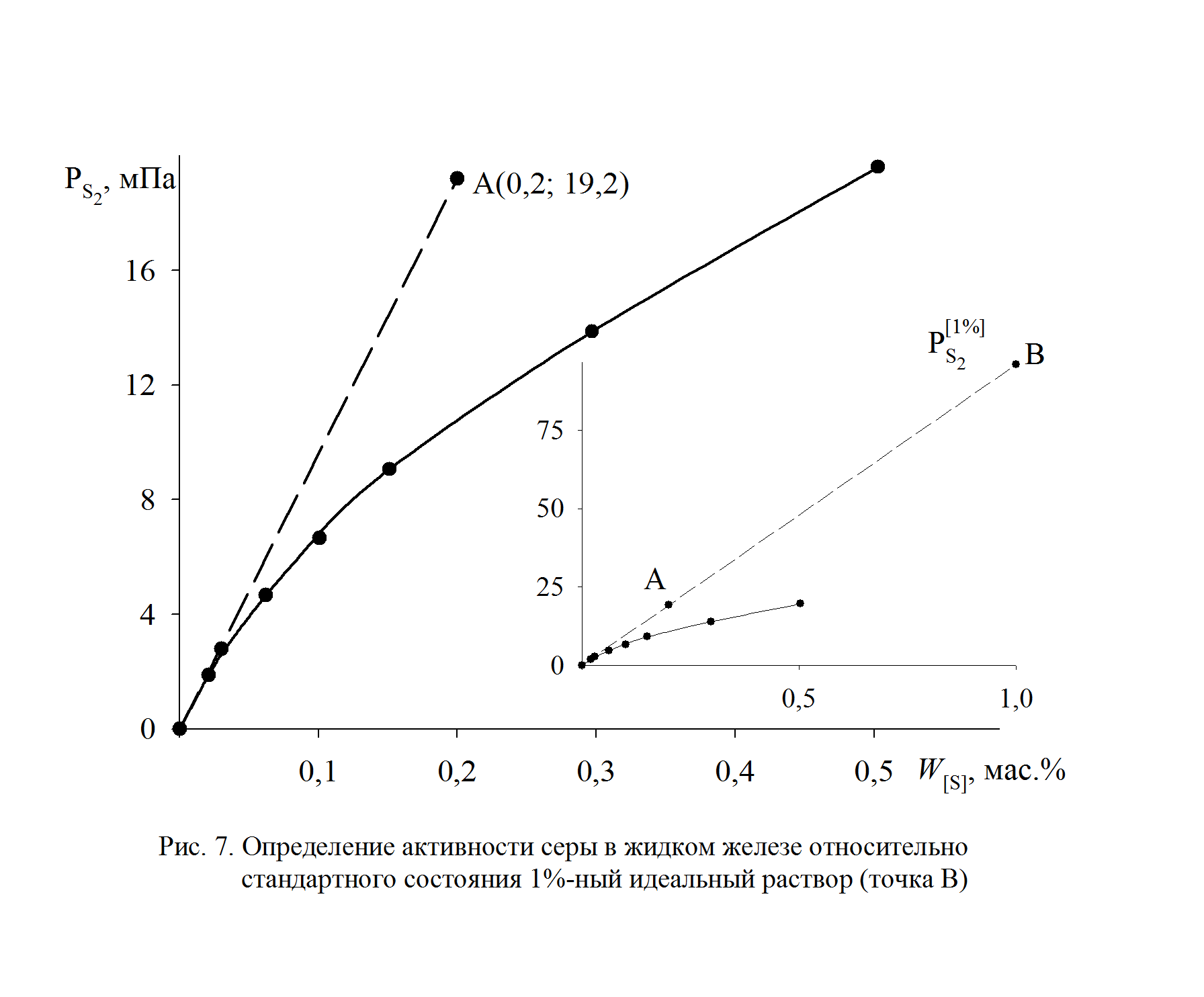
Решение. Рассмотрим несколько вариантов решения задачи. 1. При низких концентрациях примесного элемента в железе (кислород, азот, сера, фосфор и др.) чаще всего за стандартное выбирается состояние растворенного вещества в 1%-ном идеальном растворе, то есть в растворе, подчиняющемся закону Генри. Как видно из рис. 2.7, только очень разбавленный раствор серы в железе (<0,03 мас.%) становится идеальным. Следовательно, стандартный 1%-ный раствор является гипотетическим (см. точку В на рис. II.7). Для определения давления серы над стандартным раствором
Активности серы, вычисленные по формуле
представлены в таблице вместе с коэффициентами активности
Раствор серы в железе характеризуется значительными отрицательными отклонениями от закона Генри.
2. Рассчитаем активность серы относительно гипотетической чистой серы. Для этого пересчитаем концентрацию серы в молярные доли
Результаты расчетов сведены в табл. 2.8. Зависимость
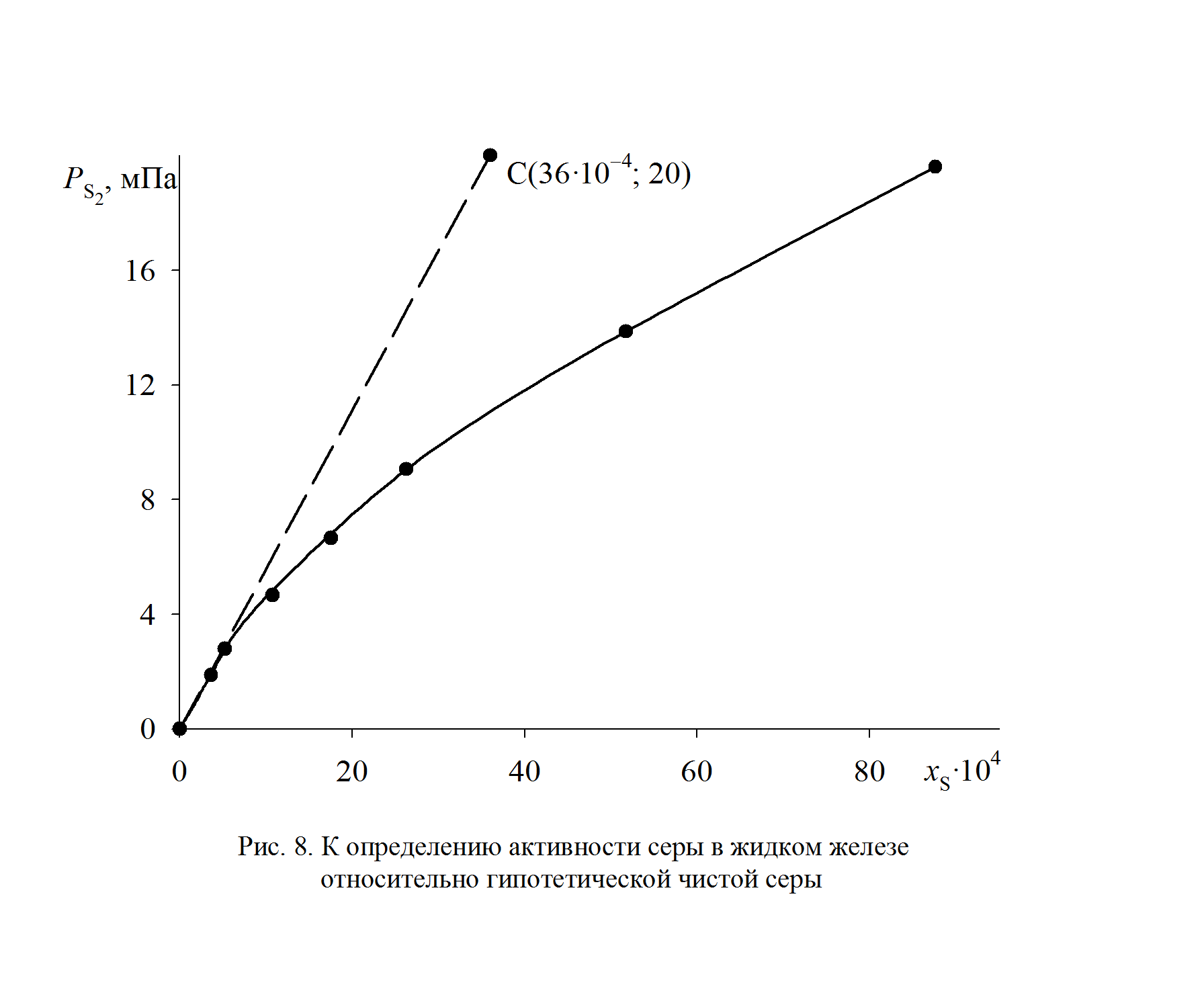
Таким образом, активность и коэффициент активности серы рассчитываются по формулам
Результаты представлены в табл. 2.8.
8.2. Определение активности растворителя по понижению Если в бинарной системе примесное вещество растворяется в жидком растворителе, но совершенно не растворяется в твердом, то при охлаждении жидкий раствор начнет кристаллизоваться при температуре более низкой, чем температура кристаллизации чистого растворителя. При этом реализуется равновесие твердых чистых кристаллов растворителя с жидким раствором строго определенного состава. Условием равновесия является равенство
где
где
При интегрировании этого уравнения
пренебрегаем зависимостью
Тогда
где Пример 2.53. В таблице 2.10 приведены температуры начала кристаллизации солевых расплавов PbCl2 – KCl. Вычислить активности и коэффициенты активности PbCl2. Теплота плавления этой соли Таблица 2.10 Экспериментальные данные и результаты расчетов
Решение. Для примера вычислим по формуле (II.36) активность PbCl2 в растворе с концентрацией
Тогда коэффициент активности
Результаты расчетов сведены в табл. 2.10. Солевой расплав PbCl2 – KCl характеризуется отрицательными отклонениями от закона Рауля. 8.3. Определение активности компонента раствора Если компонент конденсированного раствора участвует в какой-либо химической реакции, то его активность может быть вычислена по экспериментальным данным о химическом равновесии этой реакции. Например, активность углерода, растворенного в железе, может быть найдена по результатам экспериментального изучения равновесия реакции обезуглероживания [C]Fe + CO2 = 2CO. Действительно, константа равновесия этой реакции
поэтому для расчета Другой пример. Активность серы в жидком железе определяется по данным о равновесии реакции [S] + H2 = H2S, Пример 2.54. Взаимодействие солевого расплава MgCl2 – KCl с кислородом описывается реакцией (MgCl2)ж.р. + ½О2 = MgОтв. + Cl2. (a) Результаты экспериментального исследования равновесия этой реакции при температуре 1200 K представлены в таблице 2.11. Рассчитать активности и коэффициенты активности MgCl2. В твердом оксиде MgО соли MgCl2 и KCl не растворяются. Таблица 2.11 Опытные данные и результаты расчетов
Решение. Константа равновесия реакции (а)
так как а MgO = 1. Имеющиеся опытные данные позволяют рассчитать
Активности и коэффициенты активности MgCl2 в исследованных солевых расплавах определим по формулам
Результаты расчетов сведены в табл. 2.11. Пример 2.55. Равновесие реакции [C]Fe + CO2 = 2CO изучалось экспериментально при 1273 K и общем давлении равновесной газовой смеси CO – CO2 1 атм. По опытным данным (см. таблицу 2.12) вычислить активности и коэффициенты активности растворенного в g-Fe углерода. Таблица 2.12 Экспериментальные данные и результаты расчетов
* – молярная доля углерода в насыщенном растворе. Решение. По характеру имеющихся экспериментальных данных в качестве стандартного следует взять состояние углерода в насыщенном растворе
Таким образом, активности и коэффициенты активности углерода в твердом растворе можно вычислить по формулам
Например, для насыщенного раствора
а для раствора с концентрацией углерода х [C] = 2,57×10–2
Результаты расчетов представлены в табл. 2.12.
Замечание. Активности и коэффициенты активности углерода определены «по Раулю». Насыщенный раствор углерода в железе находится в равновесии с чистым твердым графитом, следовательно [C]* + CO2 = 2CO равна константе равновесия реакции взаимодействия чистого графита с углекислым газом C + CO2 = 2CO, для которой
Пример 2.56. Жидкое железо, находящееся в равновесии с чистым жидким оксидом FeO, насыщено кислородом, а растворимость кислорода (мас.%) определяется уравнением
Вычислить для температуры 1853 K активность и коэффициент активности FeO в шлаке, содержащем (мас.%) СаО – 39,18; MgO – 9,14; SiO2 – 39,76; FeO – 10,25 и Fe2O3 – 1,67. Железо, находящееся в равновесии с этим шлаком, содержит кислорода 0,048 мас.%. Влиянием Са, Mg и Si на активность кислорода пренебречь. Решение. Равновесие насыщенного кислородом железа со шлаком можно описать реакцией [O]нас + Fe = (FeO)шл , константа равновесия которой
Численное значение константы равновесия при постоянной температуре и заданных стандартных состояниях не зависит от составов металла и шлака. Определим активность железа относительно стандартного состояния "чистое жидкое железо"
так как для весьма разбавленного раствора кислорода в железе gFe» 1. Активность кислорода определим относительно стандартного состояния "1%-ный идеальный раствор"
так как для разбавленного раствора кислорода в железе Таким образом, константа равновесия
За стандартное состояние FeO выберем "чистый жидкий оксид железа". Численное значение константы равновесия K определим по параметрам равновесия железа с чистым жидким FeO
Здесь
Таким образом, активность FeO в шлаке заданного состава
Для вычисления коэффициента активности
рассчитаем молярную долю
Получаем для коэффициента активности
это означает, что поведение FeO в шлаке характеризуется положительными отклонениями от закона Рауля. 8.4. Вычисление активности компонента бинарного раствора Химические потенциалы компонентов бинарного раствора связаны между собой уравнением Гиббса – Дюгема х 1dm1 + х 2dm2 = 0, (II.37) которое позволяет вычислить активность (коэффициент активности) компонента раствора, если известна активность (коэффициент активности) другого. Рассмотренные в дальнейшем примеры связаны с использованием уравнения Гиббса-Дюгема для самого простого случая неограниченной растворимости компонентов, когда в качестве стандартного состояния можно выбрать чистые компоненты. В этом случае для обоих компонентов химические потенциалы определяются формулой
Индекс R далее будет опущен. С учетом этого соотношения уравнение Гиббса–Дюгема примет вид х 1dln а 1 + х 2dln а 2 = 0. (II.38) В таком виде уравнение Гиббса – Дюгема неудобно для расчетов, так как не позволяет использовать информацию о чистом растворителе: при х 2® 0 ln а 2® – ¥. Если же в уравнение (II.38) подставить аi = g i xi и при преобразованиях учесть, что для бинарного раствора х 1 + х 2 = 1 и х 1dln x 1 + + х 2dln x 2= 0, получим уравнение х 1dlng1 + х 2dlng2 = 0, (II.39) позволяющее рассчитать коэффициенты активности одного компонента при известных коэффициентах активности другого компонента. Для вычисления коэффициента активности растворителя имеем
а для коэффициента активности растворенного вещества
Как видно, для расчетов необходимо знать коэффициент активности растворенного вещества в бесконечно разбавленном растворе
здесь k 2 – постоянная закона Генри для разбавленных идеальных растворов, см. рис. 2.6. Если известна аналитическая зависимость коэффициента активности одного из компонентов от его концентрации, для расчетов используются формулы:
Пример 2.57. Для расплава Pb – Bi зависимость коэффициента активности свинца от его молярной доли определяется уравнением lggPb = –0,32(1 – х Pb)2, 0 £ х Pb £ 1. Найти зависимость gBi от х Bi. Решение. Искомая зависимость определяется уравнениями (II.40) и (II.42)
Используя зависимость lngPb = –2,303×0,32(1 – х Pb)2, определяем производную
Подставляя ее значение в подинтегральное выражение, получаем следующую зависимость gBi от х Bi:
Пример 2.58. Зависимость коэффициента активности алюминия от состава расплава Fe – Al при 1873 K описывается уравнением lggAl = –1,51 + 2,60 х Al , 0 £ х Al £ 0,25. Определить зависимость коэффициента активности железа от концентрации его в расплаве. Решение. После преобразований, аналогичных проделанным в предыдущем примере, уравнение (II.21) для железоалюминиевого расплава примет вид
Вычисление интеграла упрощается, если подинтегральную функцию представить следующим образом
Тогда получим
lggFe = 5,99lg x Fe + 2,6(1 – x Fe), 0,75 £ x Fe £ 1. Пример 2.59. Зависимость активности монооксида железа в оксидном расплаве FeO – Fe2O3 от ионной доли двухвалентного железа Fe2+ определяется уравнением
Определить зависимость активности Fe2O3 от ионной доли Fe3+. Решение. Если стандартными являются состояния чистых жидких оксидов FeO и Fe2O3, то по уравнению Гиббса-Дюгема
Выразим молярные доли оксидов через ионные доли катионов железа. По определению ионной долей называется отношение числа молей иона к общему числу молей ионов того же знака, то есть
Последние преобразования в этих соотношениях связаны с делением числителя и знаменателя на сумму
Таким образом,
Пример 2.60. Определенные опытным путем давления насыщенных паров цинка над бинарными расплавами Sn – Zn при температуре 973 K приведены в таблице 2.13. Рассчитать активности цинка и олова. Решение. Расчеты выполним для стандартных состояний "чистый жидкий компонент". Приведенные в табл. 2.13 величины активностей и коэффициентов активности цинка вычислялись по уравнениям
Таблица 2.13 Результаты опытов и расчетов активностей компонентов бинарных расплавов Sn – Zn
* – величины Для вычисления коэффициентов активности олова воспользуемся уравнением Гиббса – Дюгема
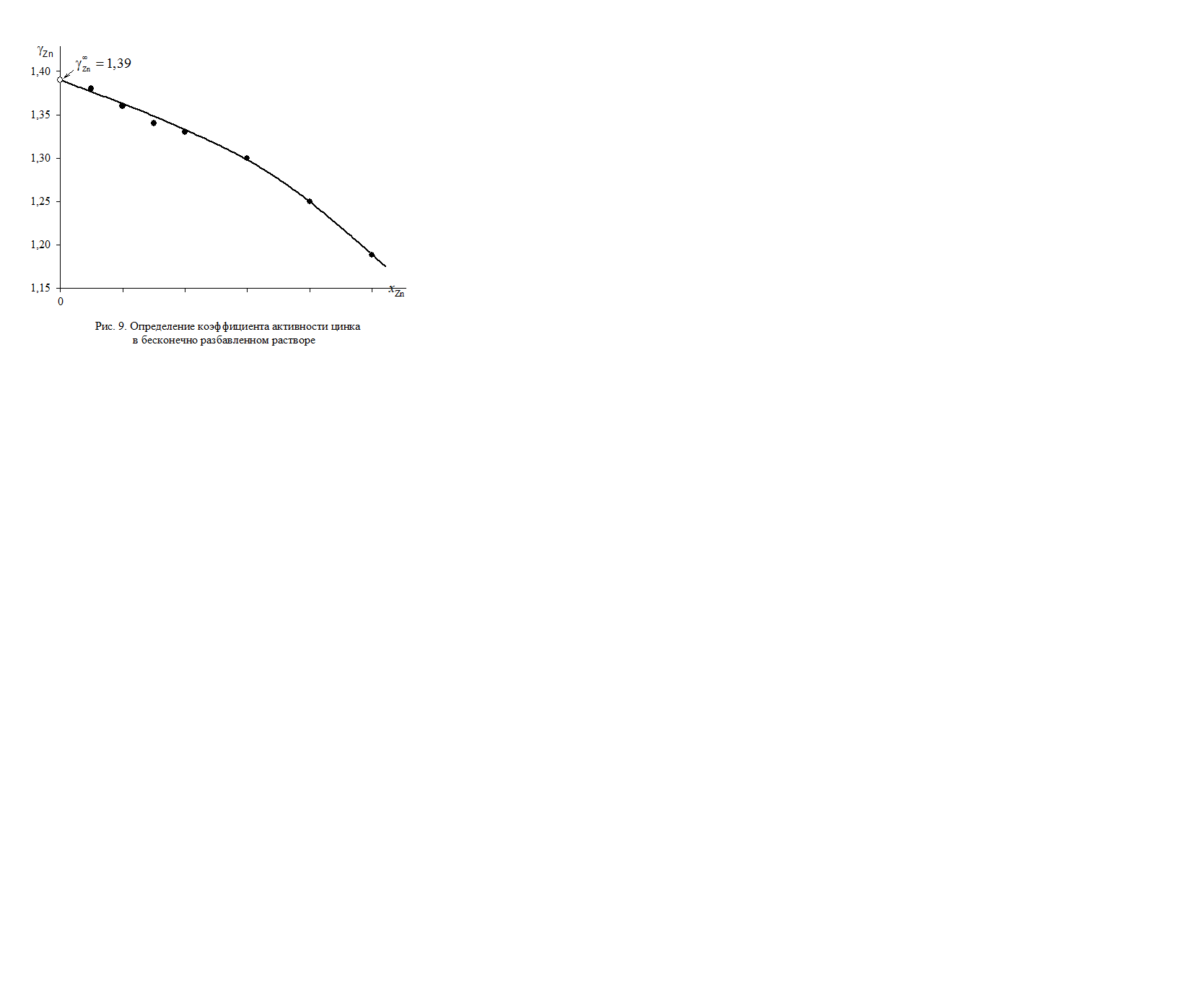
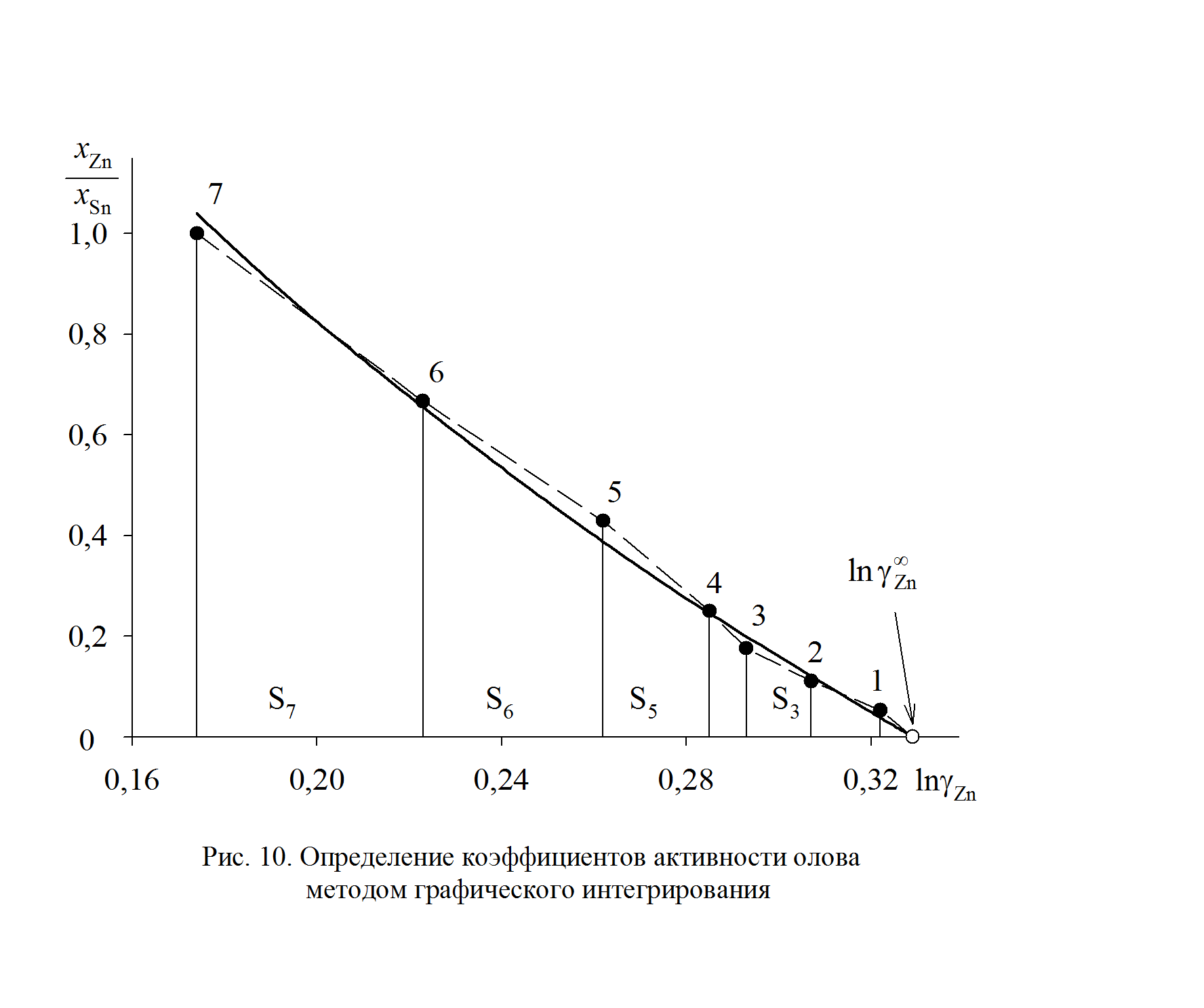
В отсутствии аналитических зависимостей (см. примеры 2.57 – 2.59) воспользуемся графическим вычислением интеграла по площади фигуры под кривой «зависимости» х Zn/ х Sn от lngZn. Величину нижнего предела интегрирования определяем либо экстраполяцией графика зависимости gZn = f (х Zn) до значения х Zn = 0 (см. рис. 2.9), либо графика зависимости х Zn/ х Sn от lngZn до значения х Zn/ х Sn = 0 (см. рис. 2.10). С учетом найденной величины
График, иллюстрирующий процедуру вычислений, представлен на рис. 2.10. Возможны два варианта расчета. В одном расчет проводится для любых заданных концентраций раствора по точкам кривой. Если же экспериментальные точки незначительно отклоняются от кривой, возможен расчет по этим точкам, то есть с использованием данных таблицы. Покажем это на примерах расчета для первых трех растворов (см. точки 1, 2 и 3 на рис. 2.10). Имеем
Для коэффициентов активности и активностей имеем
Результаты расчетов сведены в табл. 2.13 и из них следует, что расплав Sn – Zn характеризуется положительными отклонениями от закона Рауля. 8.5. Задачи для самостоятельного решения 2.120. Давления пара магния над расплавами Mg–Cu разного состава при 1000 K приведены в таблице. Определить активности магния относительно стандартного состояния «чистый жидкий магний» и характер отклонений от закона Рауля.
Ответ: а Mg = 1,0; 0,9206; 0,7333; 0,3833; 0,0793 и 0,0266. gMg = 1,0; 0,9836; 0,9586; 0,6590; 0,2403 и 0,1186. Отрицательные. 2.121. Давления пара серебра над расплавами серебро – золото при 1225 K приведены в таблице. Определить активности и коэффициенты активности серебра (стандартное состояние «чистое жидкое серебро»), а также характер отклонений от закона Рауля.
Ответ: а Аg = 1,0; 0,6854; 0,4717; 0,2546 и 0,0729. gАg = 1,0; 0,9454; 0,7608; 0,6563 и 0,3737. Отрицательные. 2.122. Зависимость давления насыщенного пара (атм) чистого цинка от температуры выражается уравнением
Вычислить активности и коэффициенты активности цинка при 973 K в сплавах Zn – Sn по экспериментальным данным, приведенным в таблице.
Ответ: а Zn = 0,7896; 0,5985; 0,5873 и 0,3194; gZn = 1,0557; 1,2091; 1,2134 и 1,3829. Положительные 2.123. Температуры начала кристаллизации хлористого магния в зависимости от состава жидких солевых расплавов MgCl2 – PbCl2 приведены в таблице. Определить активности и коэффициенты активности хлористого магния, если теплота плавления
Ответ:
2.124. Температуры начала кристаллизации магния из расплавов
Ответ: а Mg = 1,0; 0,9365; 0,8700; 0,8007 и 0,7793. gMg = 1,0; 0,9910; 0,9667; 0,9278 и 0,9115. Отрицательные. 2.125. В таблице приведены составы равновесных жидких и твердых растворов Сu – Ag при разных температурах. Вычислить активности и коэффициенты активности меди в жидких растворах Cu – Ag, если твердый раствор считать совершенным. Теплота плавления меди
Ответ: а Сu = 1,0; 0,902; 0,8504; 0,800; 0,751 и 0,681. gCu = 1,0; 1,014; 1,063; 1,160; 1,341 и 1,706. 2.126. При температуре 1873 K в несмешивающихся жидких серебре и железе концентрации меди равны соответственно 11,5 и 2,92 мол.%. Определить активности и коэффициенты активности меди в обоих растворах, если при этой температуре давление насыщенного пара чистой меди равно 1,234×10–3 атм, а над раствором Fe – Cu указанной концентрации – 2,344×10–4 атм. Ответ: а Сu = 0,19; 2.127. По данным таблицы о равновесных концентрациях кремния, распределенного при 1693 K между несмешивающимися железом и серебром, определить активности и коэффициенты активности кремния в железе, если коэффициент активности его в серебре в изученном интервале концентраций равен 0,155 (стандартное состояние – чистый кремний).
Ответ:
2.128. При 1888 K железо, равновесное с чистым монооксидом железа, содержит 0,249 мас.% кислорода. Вычислить активность и коэффициент активности монооксида железа в шлаке, содержащем 0,387 моля СаО; 0,171 MgO; 0,238 SiO2; 0,630 FeO; 0,037 Fe2O3 и 0,028 Cr2O3. Жидкое железо в равновесии с этим шлаком содержит 0,187% кислорода. Какими отклонениями от закона Рауля характеризуется монооксид железа в шлаке? Ответ: а FeO = 0,751; gFeO = 1,777; положительные. 2.129. Использовав приведенные в таблице данные о равновесии реакции [C]Fe + 2Н2 = СН4 при 1273 K (давления компонентов газовой смеси выражены в атм), вычислить активности и коэффициенты активности углерода в аустените. Стандартное состояние – гипотетический углерод и поэтому при x C ® 0
Ответ:
2.130. По данным о равновесии реакции 2(FeO) = O2 + 2Fе при 1373 K определить активности и коэффициенты активности монооксида железа в растворе FеО – MgO. Построить график зависимости активности монооксида железа от его концентрации.
Ответ: а FeO = 1,0; 0,8913; 0,822; 0,7674; 0,7244; 0,6531 и 0,4365. gFeO = 1,0; 1,0936; 1,111; 1,248; 1,342; 1,519 и 1,940. 2.131. По данным о равновесии реакции (SiO2) +3C= SiC + 2СО при 1723 K определить активности и коэффициенты активности диоксида кремния в расплавах CaO – SiO2. Какими отклонениями от закона Рауля характеризуется диоксид кремния в этой системе?
Ответ:
2.132. Для коэффициента активности цинка в сплавах кадмий – цинк при 435 °С было найдено
Найти, используя уравнение Гиббcа – Дюгема, зависимость от сосстава коэффициента активности кадмия в этих сплавах. Ответ: 2.133. Коэффициент активности цинка в медноцинковых сплавах определяется уравнением Ответ: 2.134. Коэффициент активности цинка в жидкой бронзе определяется уравнением Ответ: 3,281×10–4 атм. 2.135. Твердый сплав, содержащий 10 мол.% никеля и 90 мол.% золота, при 1000 K реагирует с водяным паром с образованием NiO. Реакция достигает равновесия, когда пароводородная смесь содержит 0,35 об.% водорода. Найти коэффициент активности никеля в растворе при 1000 K, используя следующие данные:
Ответ: 5,957. 2.136. Для системы Cd – Рb зависимость коэффициента активности кадмия от состава описывается уравнением
если за стандартное состояние выбрать гипотетический жидкий кадмий. Рассчитать активности кадмия в растворах, для которых х Cd равно 0,2 и 0,4. Ответ: 0,139 и 0,199. 2.137. Зависимость активности монооксида железа в расплаве FeO – Fe2O3 от ионной доли трехвалентного железа при 1873 K описывается уравнением Ответ: 2.138. В расплаве FeO – SiO2 при
Определить при 1873 K активность SiO2 в расплаве FeO – SiO2 относительно твердого диоксида кремния, если Ответ: 0,685. 2.139. При 1873 K насыщенный раствор Fе – С содержит 5,3 маc.%углерода. Определить активность углерода по отношению к графиту (по Раулю), если для стандартного состояния «гипотетический углерод» (по Генри) Ответ: 2.140. Давление насыщенного пара магния над расплавами магний – свинец при 1000 K приведено в таблице. Построить график p Mg = f (x Mg) и определить: 1) характер отклонений от закона Рауля и закона Генри; 2) активность магния в растворе с молярной долей магния 0,55.
Ответ: отрицательные (Рауль), положительные (Генри), 2.141. Зависимости давлений насыщенного пара серебра от температуры над раствором Ag – Au, содержащем 22,5 мол.% серебра, и над чистым серебром описываются уравнениями:
Определить температуру, при которой для раствора указанного состава для серебра соблюдается закон Рауля. Ответ: 1550 K. 2.142. Зависимость парциальной молярной энтальпии и энтропии растворения таллия от состава расплавов Au – Tl при 1073 K приведена в таблице.
Определить характер отклонений от закона Рауля и закона Генри для таллия. Ответ: отрицательные (Рауль), положительные Генри), так как 2.143. По зависимости давления насыщенного пара меди от состава железо – медных расплавов при 1823 K:
вычислить значения активностей и коэффициентов активности меди, построить графики зависимости их от состава и оценить величину коэффициента активности меди в бесконечно разбавленном растворе Ответ: a Cu = 1; 0,922; 0,888; 0,870; 0,820; 0,730; 0,424; 0,182; 0,119;
2.144. При температуре 1933 K железо, равновесное с чистым FeO, содержит 0,292 мас.% кислорода. Вычислить активность и коэффициент активности монооксида железа в шлаке следующего состава: 14,4 – CaO; 8,6 – MgO; 14,1 – SiO2; 54,0 – FeO; 4,7 – Fe2O3; 4,2 мас.% Cr2O3. Жидкое железо в равновесии с этим шлаком содержит 0,243 мас.% кислорода. Ответ: 0,832; 1,674. 2.145. При 1913 K железо, равновесное с чистым FeO, содержит 0,269 мас.% кислорода. Вычислить активность и коэффициент активности монооксида железа в шлаке следующего состава: 18,52 – CaO; 6,86 – MgO; 13,34 – SiO2; 37,41 – FeO; 11,22 – Fe2O3; 10,64 мас.% Cr2O3. Жидкое железо в равновесии с этим шлаком содержит 0,181 мас.% кислорода. Ответ: 0,673; 1,785. 2.146. По данным о равновесии реакции
определить активности и коэффициенты активности оксида железа в растворах FeO – MgO. Построить графики зависимостей Ответ: a FeO = 1; 0,871; 0,822; 0,767; 0,710; 0,661; 0,543; 0,457; 0,275; 0,114; gFeO = 1; 1,062; 1,126; 1,181; 1,245; 1,436; 1,698; 1,793; 2,040; 2,522. 2.147. По данным о равновесии реакции
определить активности и коэффициенты активности кремнезема в растворах CaO – SiO2. Ответ:
2.148. Равновесие реакции взаимодействия углерода,растворенного в аустените стали «Fe – Mn(4,04%) – C» при 1273 K [C] + 2H2 = CH4 характеризуется параметрами, приведенными в таблице. Определить константу равновесия реакции, активности и коэффициенты активности углерода в трехкомпонентном твердом растворе. Стандартное состояние – гипотетический углерод, следовательно, при х [С] ® 0
Ответ: K = 0,079 атм–1;
2.149. Равновесие реакции [S]Fe + H2 = H2S изучалось при 1883 K (см. табл.).
Определить константу равновесия реакции, вычислить активности и коэффициенты активности серы в жидком железе. Стандартное состояние – гипотетическая сера и, следовательно, при х [S] ® 0 Ответ: K = 0,1467;
2.150. При температуре 523 K коэффициент активности олова зависит от состава его сплавов с ртутью
Определить зависимость коэффициента активности ртути от состава. Ответ: 2.151. При температуре 1873 K коэффициент активности углерода зависит от состава железоуглеродистых расплавов
Определить зависимость коэффициента активности железа от состава раствора. Ответ: 2.152. Зависимость активности углерода от состава аустенита описывается уравнением
Определить зависимость активности g-Fe от состава. Ответ: 2.153. В расплавах Ag–Au при 1300 K парциальная молярная энтропия растворения серебра равна таковой для совершенного раствора D S = – R (x Ag ×ln x Ag + x
|

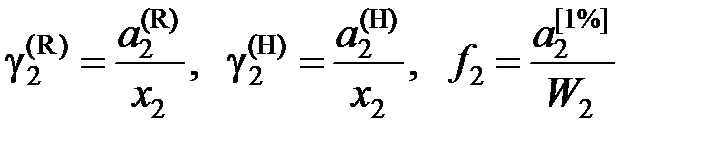 . (II.30)
. (II.30)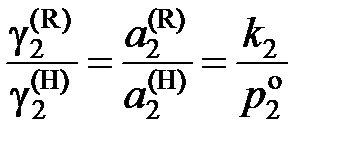 ; (II.31)
; (II.31)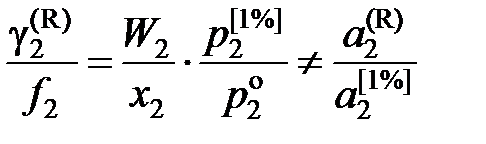 ; (II.32)
; (II.32)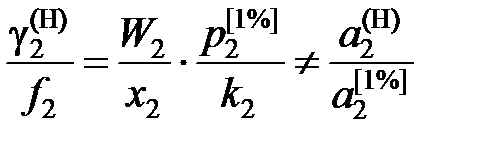 . (II.33)
. (II.33)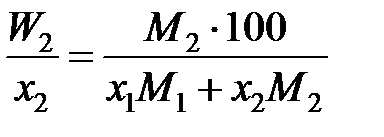 , (II.34)
, (II.34)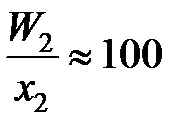 , следовательно, и отношение коэффициентов активностей постоянными. Для достаточно разбавленных растворов любых бинарных систем
, следовательно, и отношение коэффициентов активностей постоянными. Для достаточно разбавленных растворов любых бинарных систем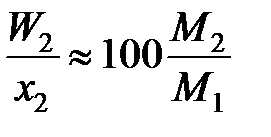 ,
,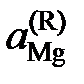
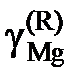
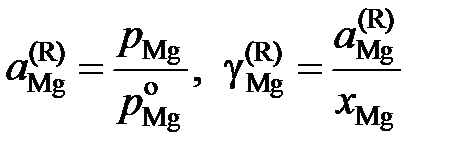 ,
,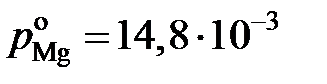 атм. Результаты вычислений представлены в табл. 2.8. Видно, что
атм. Результаты вычислений представлены в табл. 2.8. Видно, что 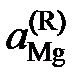 < x Mg,
< x Mg, 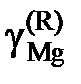 < 1 во всем исследованном интервале составов, следовательно, расплавы Mg – Pb при 1000 K характеризуются отрицательными отклонениями от закона Рауля.
< 1 во всем исследованном интервале составов, следовательно, расплавы Mg – Pb при 1000 K характеризуются отрицательными отклонениями от закона Рауля.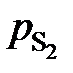 , мПа
, мПа
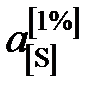
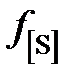
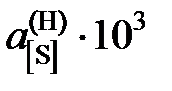
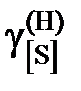
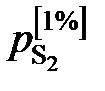 необходимо к кривой зависимости
необходимо к кривой зависимости 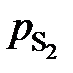 от W [S] провести касательную в точке W [S] = 0% и определить ее угловой коэффициент (по координатам, например, точки А)
от W [S] провести касательную в точке W [S] = 0% и определить ее угловой коэффициент (по координатам, например, точки А)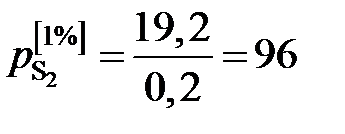 мПа.
мПа.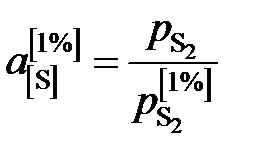 ,
,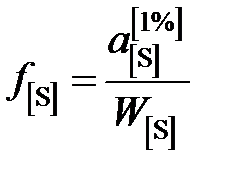 .
.
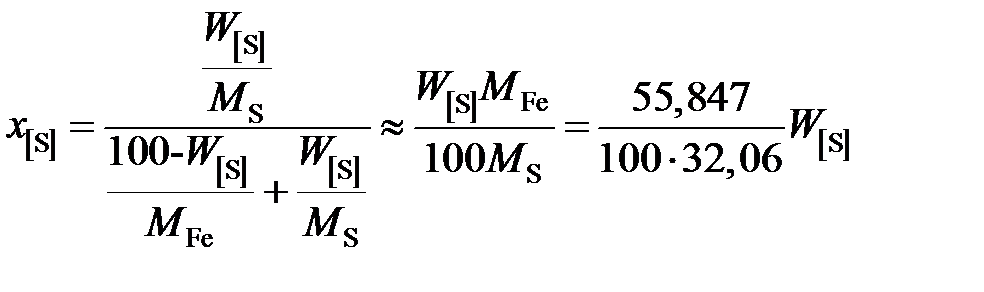 .
.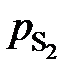 от х [S], представленная на рис. 2.8, не линейная и характеризуется отрицательными отклонениями от закона Генри (пунктирная линия). Для вычисления активности по уравнению (II.26) необходимо знать константу Генри, которую определим по координате точки С
от х [S], представленная на рис. 2.8, не линейная и характеризуется отрицательными отклонениями от закона Генри (пунктирная линия). Для вычисления активности по уравнению (II.26) необходимо знать константу Генри, которую определим по координате точки С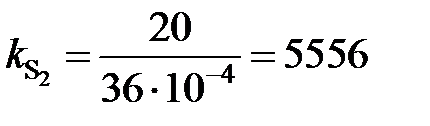 мПа.
мПа.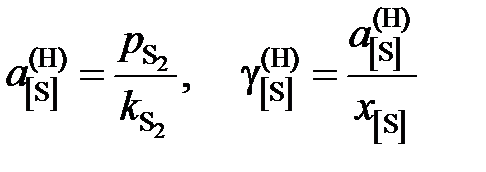 .
.
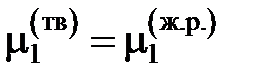 ,
,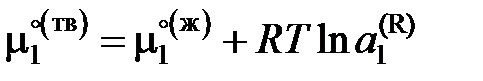 , (II.35)
, (II.35)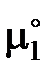 – химические потенциалы чистого растворителя,
– химические потенциалы чистого растворителя, 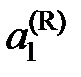 – активность растворителя в равновесном жидком растворе с молярной долей х 1 при температуре начала его кристаллизации. Разделим обе части уравнения (II.35) на температуру и продифференцируем
– активность растворителя в равновесном жидком растворе с молярной долей х 1 при температуре начала его кристаллизации. Разделим обе части уравнения (II.35) на температуру и продифференцируем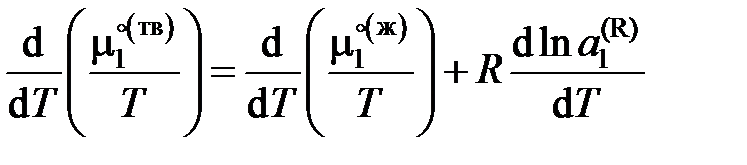 ,
,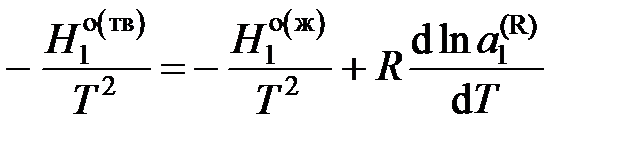 ,
,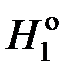 – мольные энтальпии чистого растворителя при температуре кристаллизации раствора Т. Учитывая, что
– мольные энтальпии чистого растворителя при температуре кристаллизации раствора Т. Учитывая, что 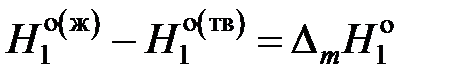 — молярная теплота плавления растворителя, получаем
— молярная теплота плавления растворителя, получаем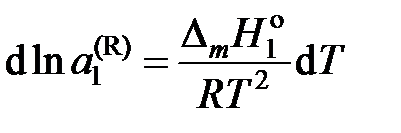 .
.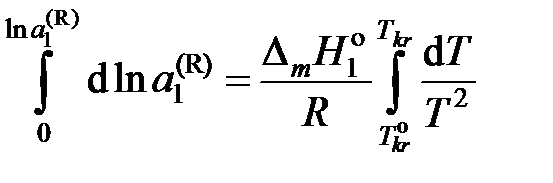
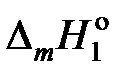 от температуры и считаем
от температуры и считаем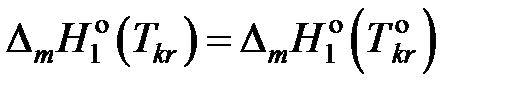 .
.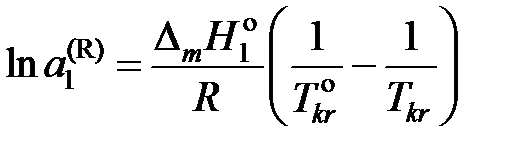 , (II.36)
, (II.36)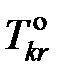 – температура кристаллизации чистого растворителя, Тkr – температура начала кристаллизации раствора, активность растворителя в котором
– температура кристаллизации чистого растворителя, Тkr – температура начала кристаллизации раствора, активность растворителя в котором 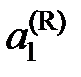 .
.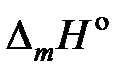 (PbCl2) = 24,29 кДж/моль.
(PbCl2) = 24,29 кДж/моль.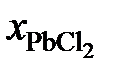
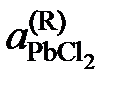
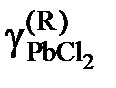
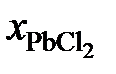 = 0,9:
= 0,9: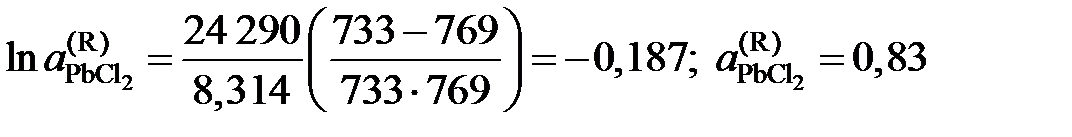 .
.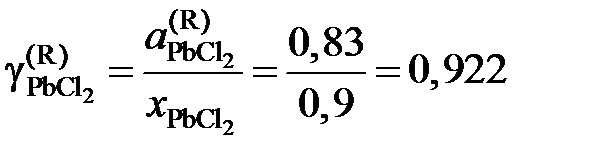 .
.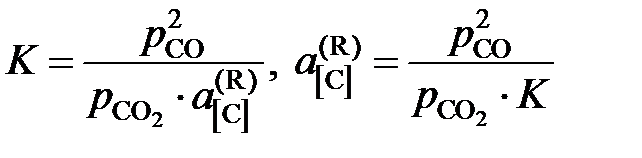 ,
,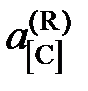 следует при известной K найти состав газовой фазы, находящейся в равновесии с исследуемым раствором.
следует при известной K найти состав газовой фазы, находящейся в равновесии с исследуемым раствором.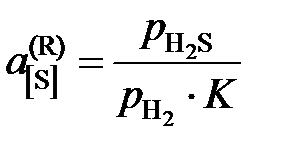 .
.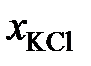
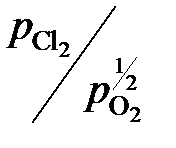 , (атм)½
, (атм)½
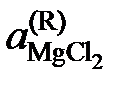
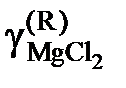
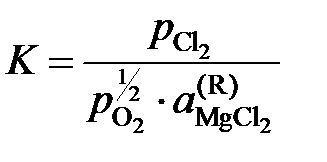 ,
,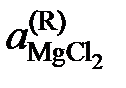 относительно стандартного состояния "чистый жидкий хлорид MgCl2". Действительно, константа равновесия не зависит от состава раствора, поэтому
относительно стандартного состояния "чистый жидкий хлорид MgCl2". Действительно, константа равновесия не зависит от состава раствора, поэтому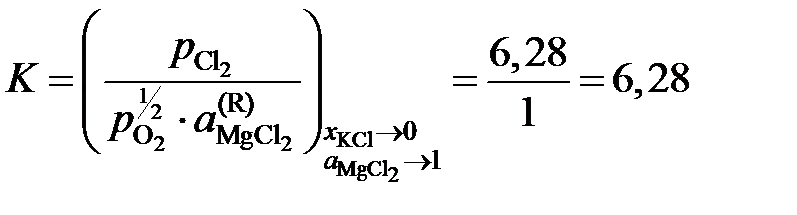 (атм)½.
(атм)½.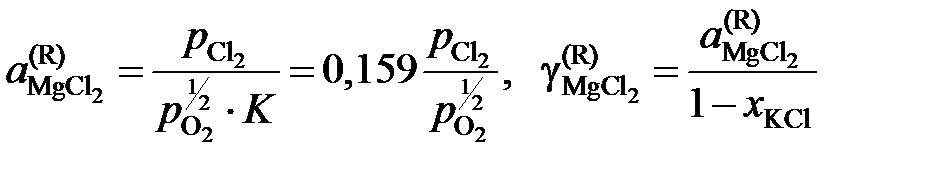 .
.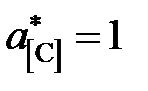 . Тогда константа равновесия реакции
. Тогда константа равновесия реакции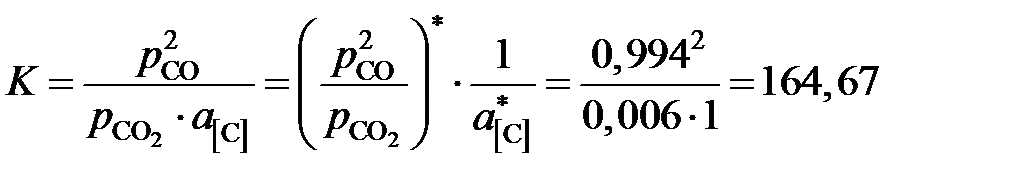 (атм).
(атм).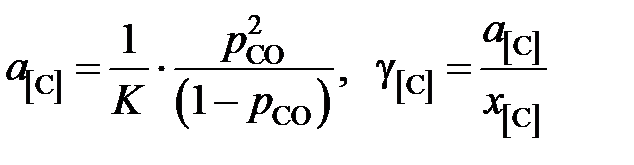 .
.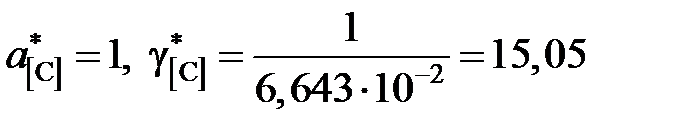 ;
;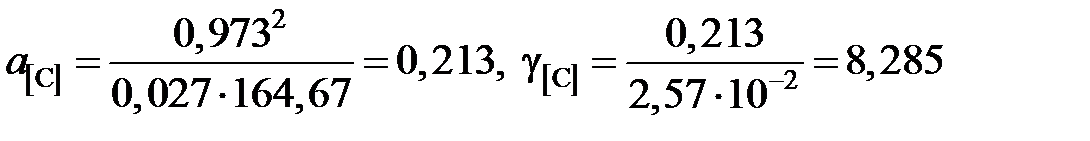 .
.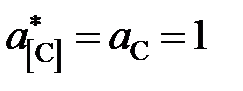 . Поэтому константа равновесия реакции
. Поэтому константа равновесия реакции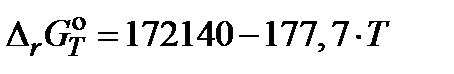 (Дж). Согласно этим данным константа равновесия при 1273 K
(Дж). Согласно этим данным константа равновесия при 1273 K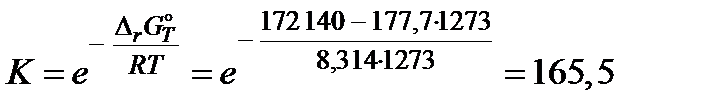 (атм).
(атм).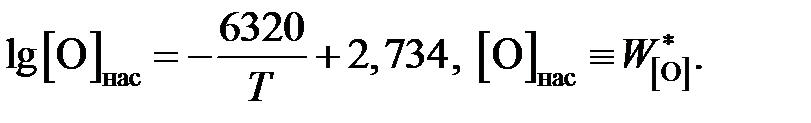
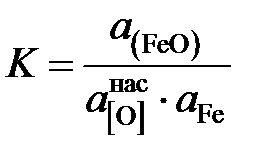 .
.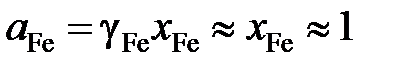 ,
,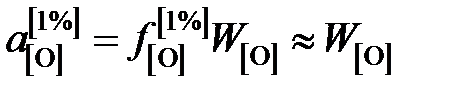 ,
,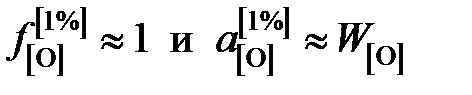 .
.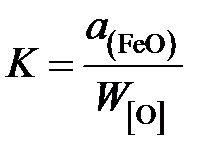 .
.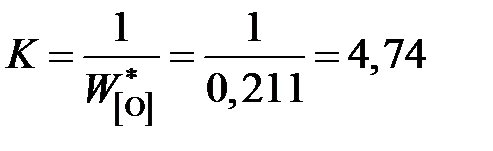 .
.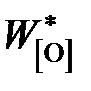 – концентрация кислорода в железе, равновесным с чистым FeO:
– концентрация кислорода в железе, равновесным с чистым FeO: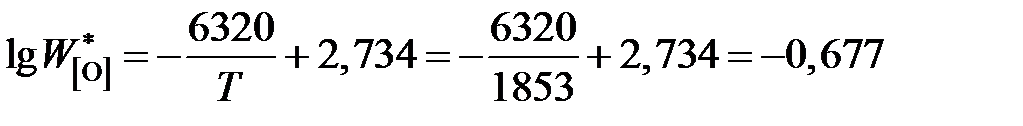 ;
;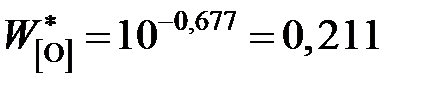 мас.%.
мас.%.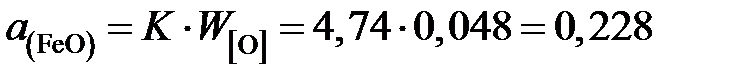 .
.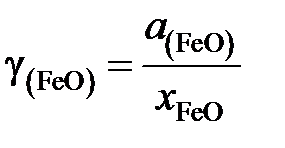
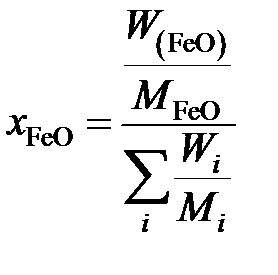 ,
,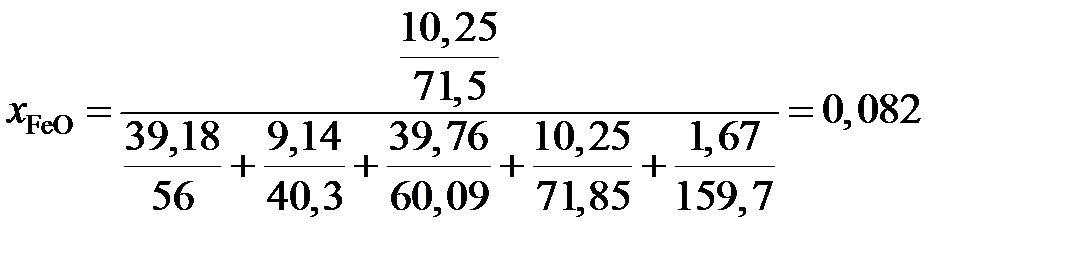 .
.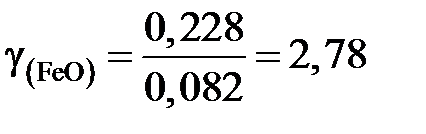 ;
;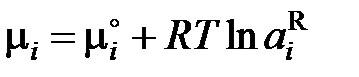 .
.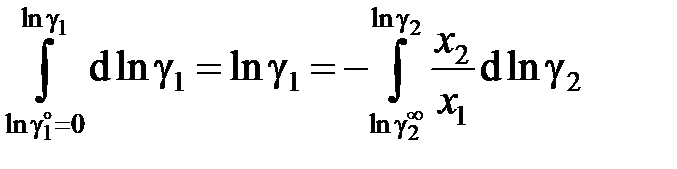 , (II.40)
, (II.40)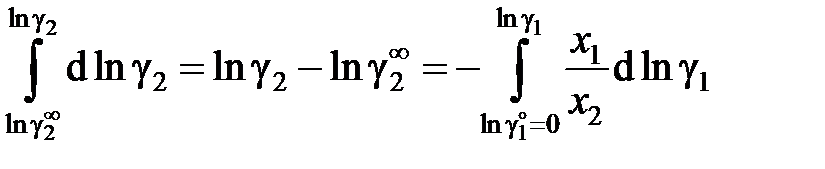 . (II.41)
. (II.41)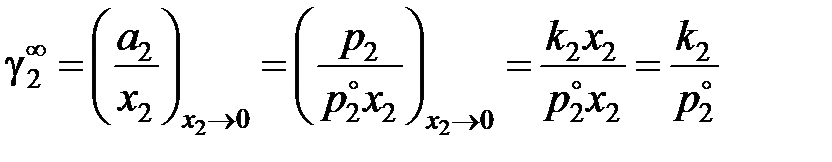 ,
,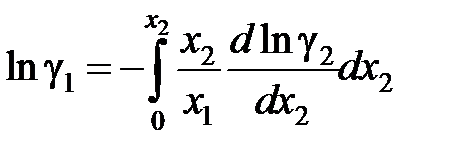 , (II.42)
, (II.42)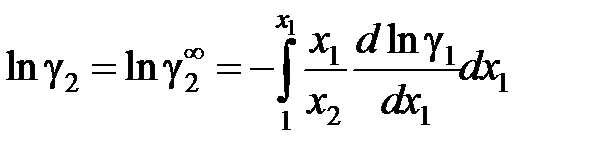 . (II.43)
. (II.43)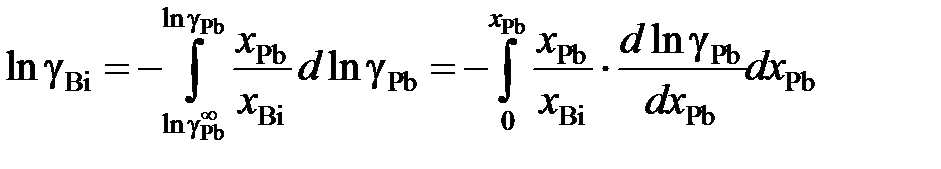 .
.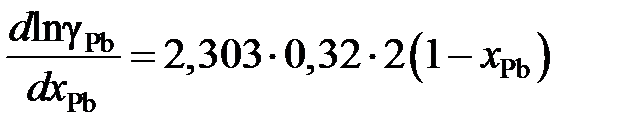 .
.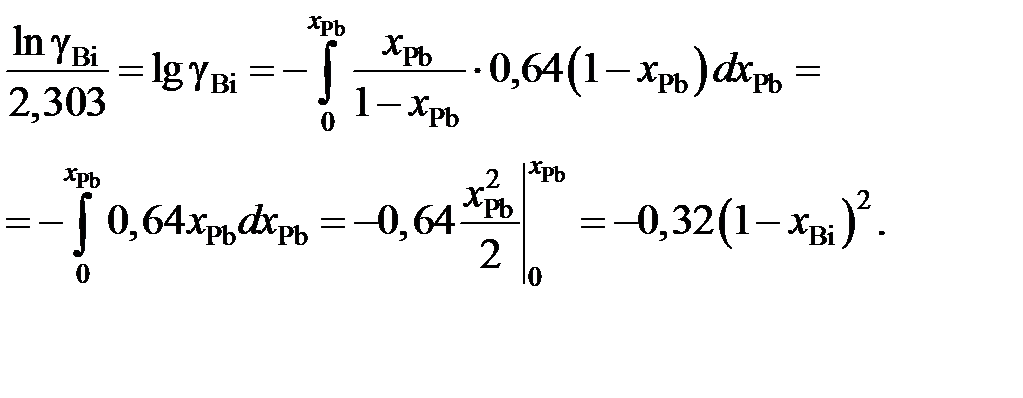
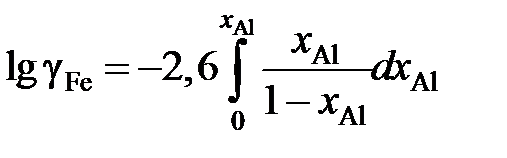 .
.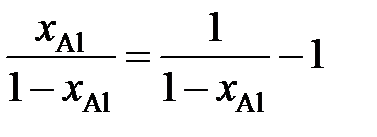 .
.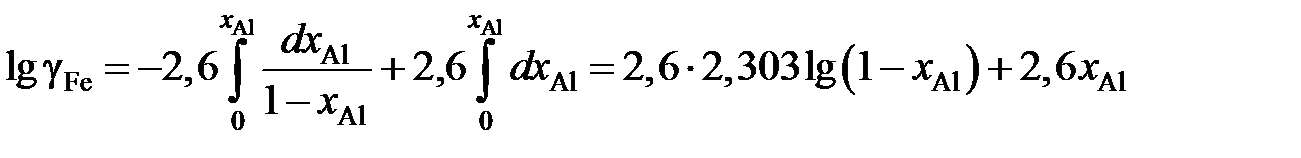 ;
;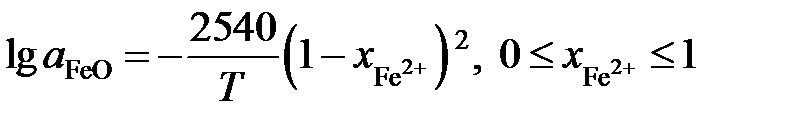 .
.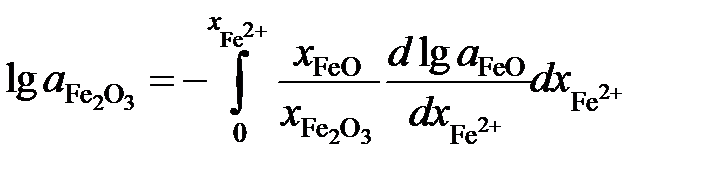 .
.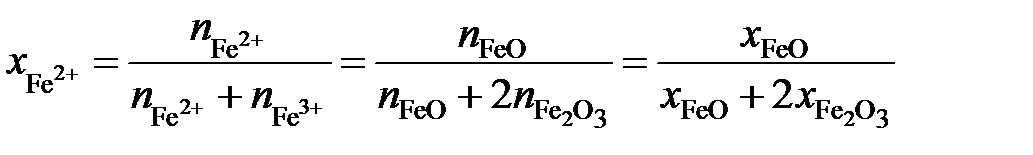 ,
,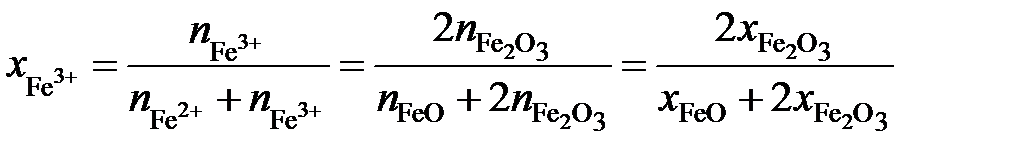 .
.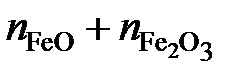 . Если учесть, что
. Если учесть, что 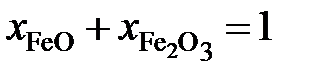 и
и 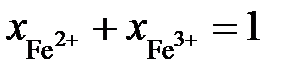 , получим
, получим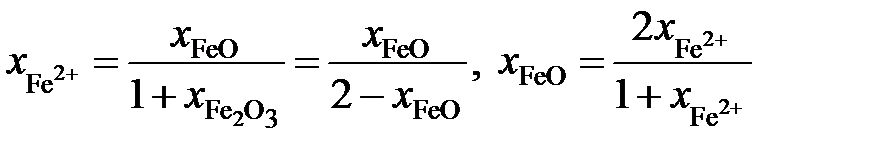 ;
;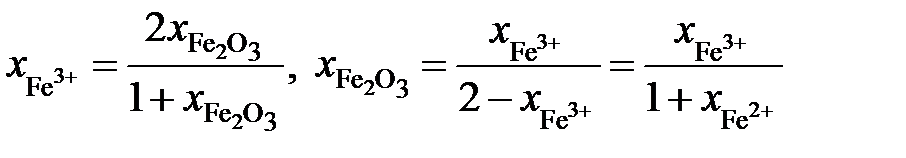 .
.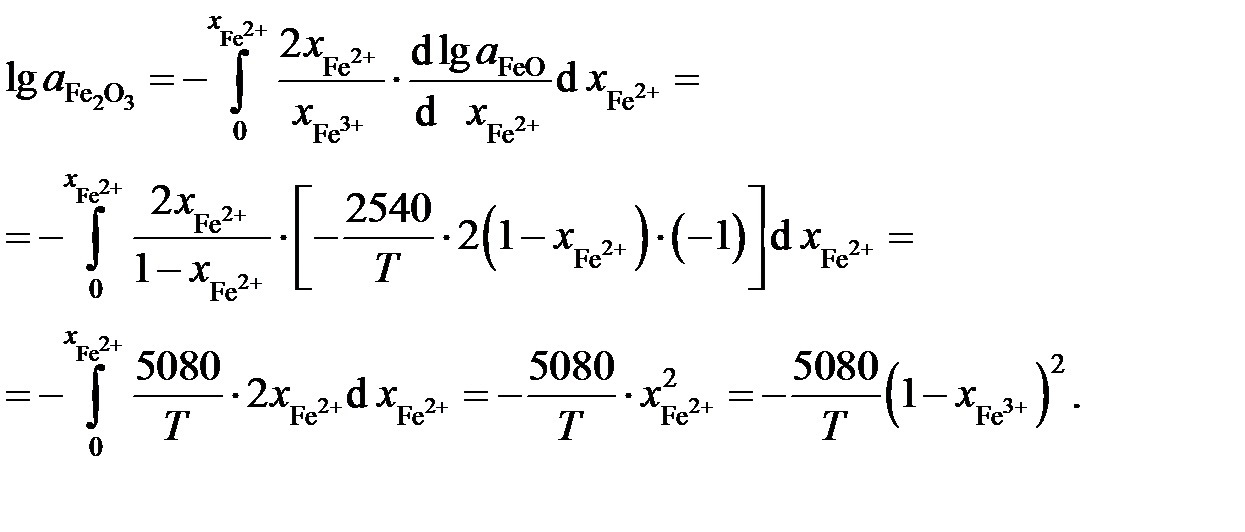
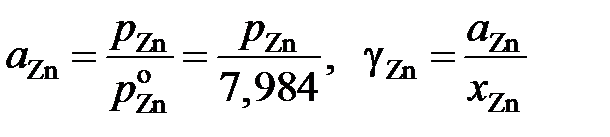 .
.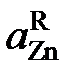
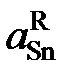
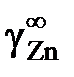 и ln
и ln 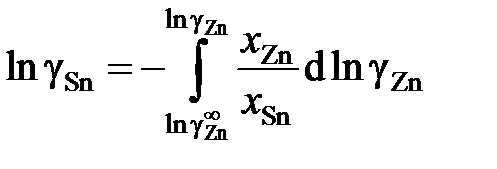 .
.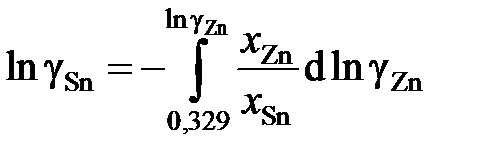 .
.
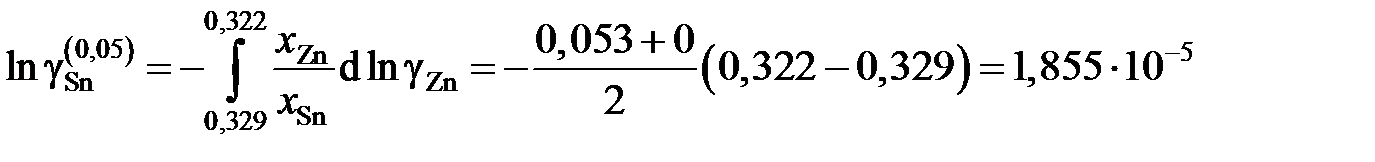 ;
;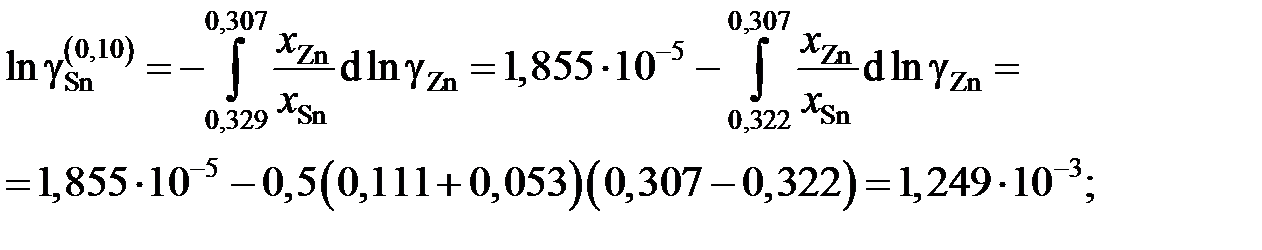
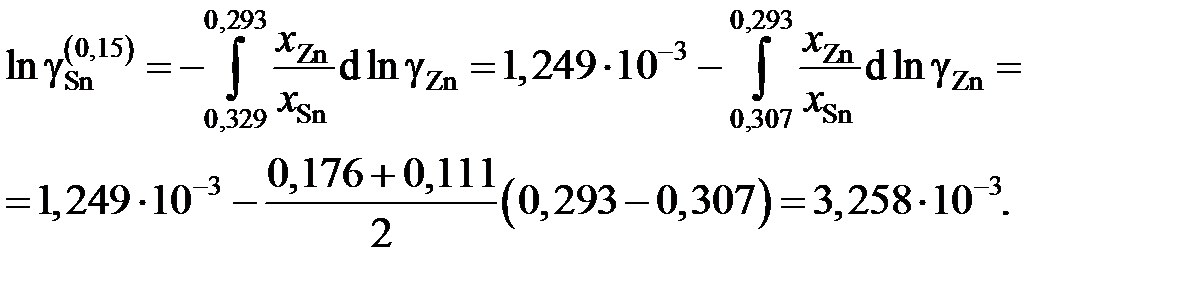
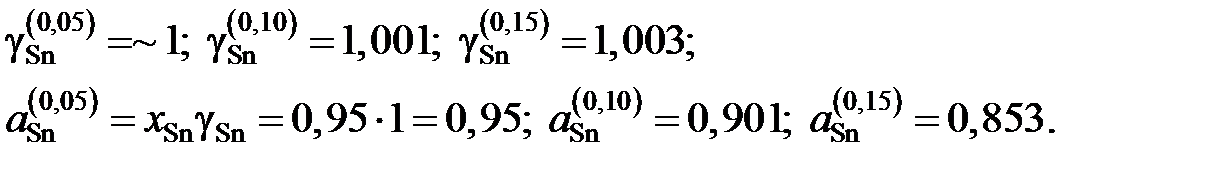
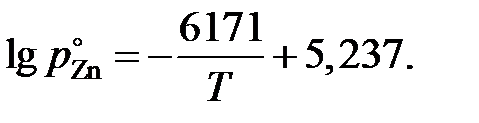
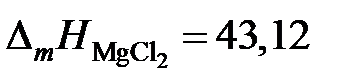 кДж/моль.
кДж/моль.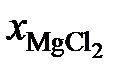
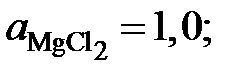 0,8192; 0,7064; 0,5120; 0,3569 и 0,2565;
0,8192; 0,7064; 0,5120; 0,3569 и 0,2565;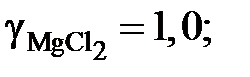 0,9153; 0,8410; 0,6764; 0,5135 и 0,3922.
0,9153; 0,8410; 0,6764; 0,5135 и 0,3922.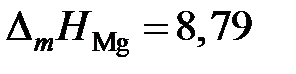 кДж/моль.
кДж/моль.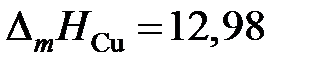 кДж/моль.
кДж/моль.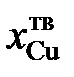
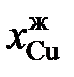
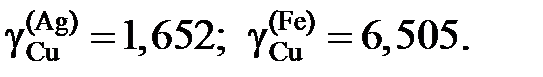
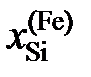
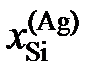
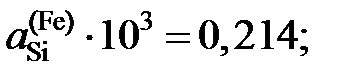 1,070; 1,178 и 6,185.
1,070; 1,178 и 6,185.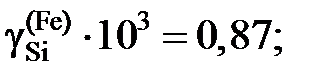 3,45; 3,68 и 15,08.
3,45; 3,68 и 15,08.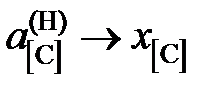 ,
, 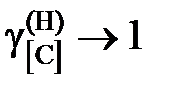 . Каковы отклонения от закона Генри?
. Каковы отклонения от закона Генри?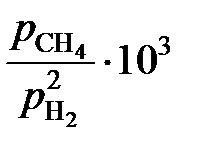
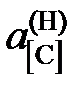 = 0,05481; 0,03278; 0,0244, 1,313, 0,708 далее
= 0,05481; 0,03278; 0,0244, 1,313, 0,708 далее 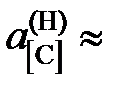 х [С].
х [С].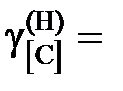 1,173; 1,093; 1,061 далее
1,173; 1,093; 1,061 далее 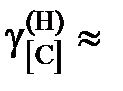 1. Положительные.
1. Положительные.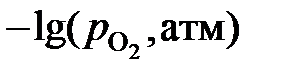
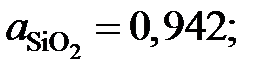 0,88; 0,66 и 0,643
0,88; 0,66 и 0,643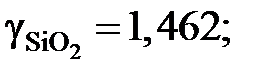 1,541; 1,838 и 2,035. Положительные.
1,541; 1,838 и 2,035. Положительные.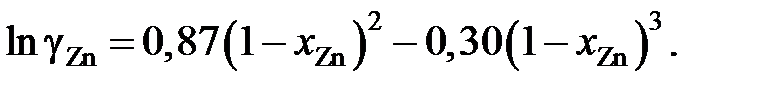
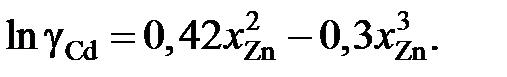
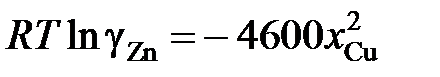 (R = 1,987 кал/моль×K). Найти, используя уравнение Гиббса – Дюгема, зависимость от концентрации коэффициента активности меди при 1500 K.
(R = 1,987 кал/моль×K). Найти, используя уравнение Гиббса – Дюгема, зависимость от концентрации коэффициента активности меди при 1500 K.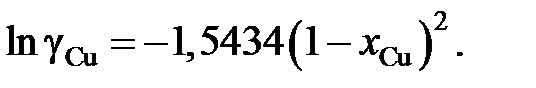
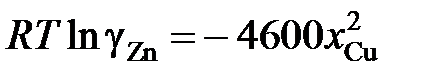 (R = 1,987 кал/моль×K). Вычислить парциальное давление паров меди при 1500 K над раствором, содержащим 40 мол.% Zn. При 1500 K давление пара чистой меди равно 7×10–4 атм
(R = 1,987 кал/моль×K). Вычислить парциальное давление паров меди при 1500 K над раствором, содержащим 40 мол.% Zn. При 1500 K давление пара чистой меди равно 7×10–4 атм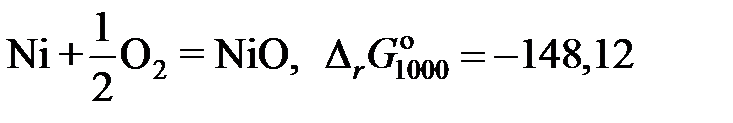 кДж;
кДж;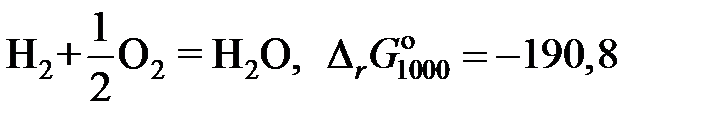 кДж.
кДж.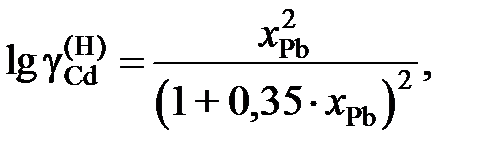
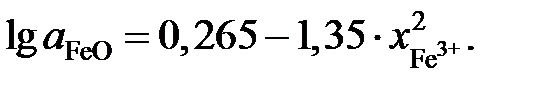 Определить состав раствора, выбранного за стандартный.
Определить состав раствора, выбранного за стандартный.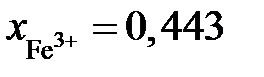 или 47 мас.% Fe2O3;
или 47 мас.% Fe2O3; 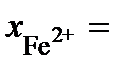 0,557 или 53 мас.% FeO.
0,557 или 53 мас.% FeO.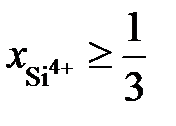 зависимость активности SiO2 от ионной доли кремния описывается уравнением
зависимость активности SiO2 от ионной доли кремния описывается уравнением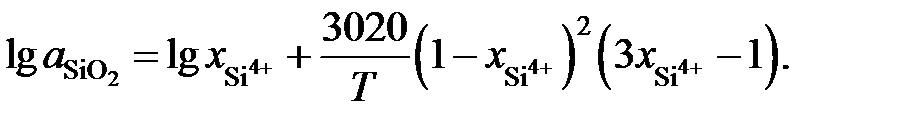
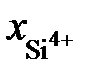 = 0,44. Известно, что при этой температуре в насыщенном диоксидом кремния расплаве содержится 52,9 мас.% SiO2.
= 0,44. Известно, что при этой температуре в насыщенном диоксидом кремния расплаве содержится 52,9 мас.% SiO2.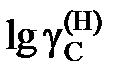 = 4,3× х C.
= 4,3× х C.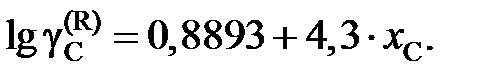
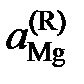 = 0,195.
= 0,195.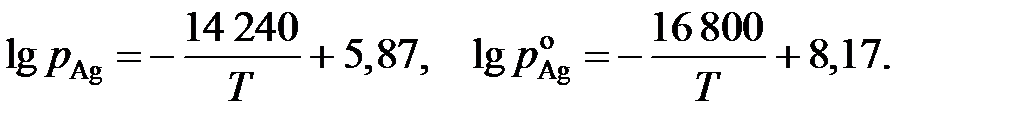
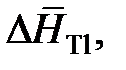 Дж/моль
Дж/моль
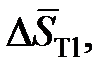 Дж/моль×K
Дж/моль×K
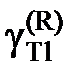 < 1.
< 1. p Cu ×;104, бар
p Cu ×;104, бар
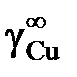 . Стандартное состояние – чистая жидкая медь.
. Стандартное состояние – чистая жидкая медь.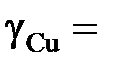 1; 1,044; 1,121; 1,389; 1,757; 3,363; 6,949; 7,930; 7,956;
1; 1,044; 1,121; 1,389; 1,757; 3,363; 6,949; 7,930; 7,956; 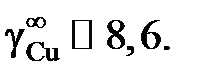
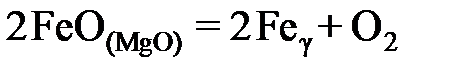 при 1573 K
при 1573 K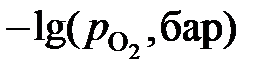
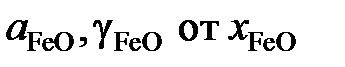 .
.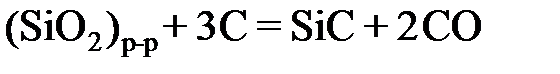 при 1773 K
при 1773 K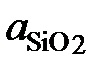 : 1; 0,356; 0,198; 0,057; 0,0166; 0,00734;
: 1; 0,356; 0,198; 0,057; 0,0166; 0,00734;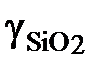 : 1; 0,553; 0,346; 0,111; 0,0362; 0,0176.
: 1; 0,553; 0,346; 0,111; 0,0362; 0,0176.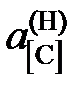 ® х [С] и
® х [С] и 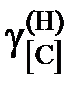 ® 1.
® 1.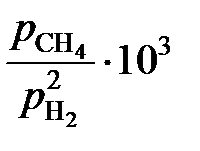 , атм –1
, атм –1
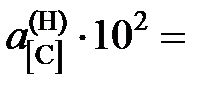 7,65; 7,03; 6,72; 4,01; 2,86; 1,61; 0,76.
7,65; 7,03; 6,72; 4,01; 2,86; 1,61; 0,76.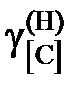 = 1,443; 1,367; 1,358; 1,163; 1,088; 1,044; 1,014.
= 1,443; 1,367; 1,358; 1,163; 1,088; 1,044; 1,014.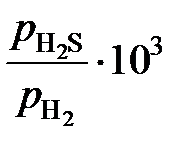
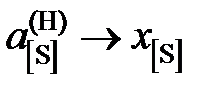 и
и 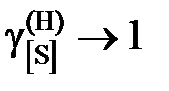 . Построить графики зависимостей активности и коэффициента активности от состава.
. Построить графики зависимостей активности и коэффициента активности от состава.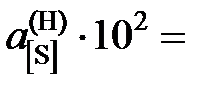 5,8; 4,9; 3,8; 3,0; 2,3; 2,0; 1,9; 1,7; далее
5,8; 4,9; 3,8; 3,0; 2,3; 2,0; 1,9; 1,7; далее 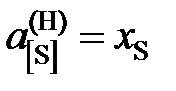 .
.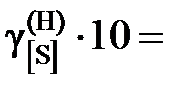 8,11; 8,73; 9,05; 9,71; 9,74; 9,77; 9,96; 9,99; далее
8,11; 8,73; 9,05; 9,71; 9,74; 9,77; 9,96; 9,99; далее 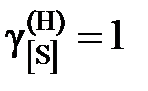 .
.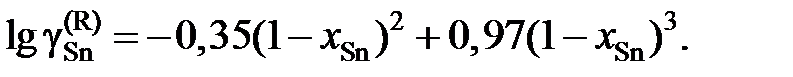
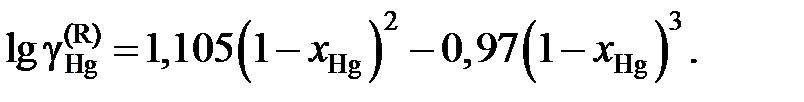
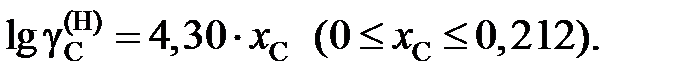
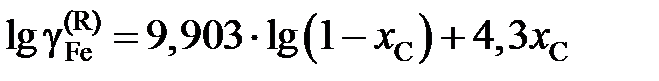 или
или 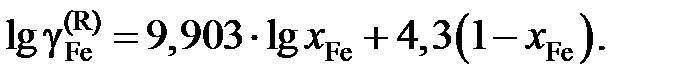
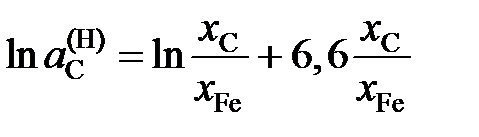
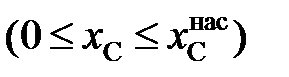 .
.