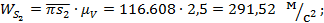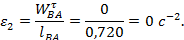Схема механизма и исходные данные
Рисунок 1- Задание №1
Для механизма компрессора даны: H = 360 мм – ход поршня; Vср = 4,8 м/с – средняя скорость поршня;
λ; = 0,25 – отношение длинны кривошипа к длине шатуна. Первоочередной задачей проектирования кривошипно-ползунного механизма является его синтез, т. е. определение размеров звеньев по некоторым первоначально заданным параметрам:
Масштаб длины Длина звена AB на чертеже:
Структурный анализ механизма
Степень подвижности механизма определяем по формуле Чебышева для плоских механизмов: W = 3∙n– 2∙p5– p4, где n= 3 – число подвижных звеньев механизма; p5= 4 – число низших кинематических пар; p4= 0 – число высших кинематических пар. Тогда:
Формула строения механизма имеет вид:
По классификации Ассура - Артоболевского данный механизм является механизмом 2-го класса. Разложение механизма на группы Ассура и входное звено показано на рис.1
Рисунок 2 – Кинематическая схема механизма
Планы скоростей Кинематическое исследование механизма начинаем с механизма 1-го класса. Для входного звена определяем угловую скорость
Масштаб плана скоростей Скорость точки B определяют из векторного уравнения:
Скорость центра масс звена 2 и находим по теореме подобия.
Значения линейных и угловых скоростей точек и звеньев определяем через отрезки плана скоростей:
Вычисления:
Планы ускорений
Определяем ускорение точки A. Так как
Вектор нормального ускорения звена направлен вдоль звена OA от точки A к точке O (к центру относительного вращения звена).
Масштаб плана ускорений Ускорение точки B:
Величины нормальных ускорений:
Вычисления:
положение 7 положение 6
Ускорения Значения полных, относительных и угловых ускорений точек и звеньев определяем через отрезки плана ускорений
Направления угловых ускорений определяем тем же методом, что и угловые скорости (через вектор касательного ускорения относительного движения точек B и D).
Вычисления:
|


 – положение центра масс;
– положение центра масс;
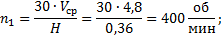


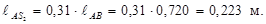


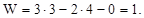


 и линейную скорость
и линейную скорость  точки A:
точки A: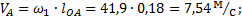
 Вектор скорости
Вектор скорости 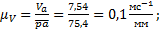




 (Большими буквами обозначаются реальные длины отрезков, малыми длины на чертеже)
(Большими буквами обозначаются реальные длины отрезков, малыми длины на чертеже)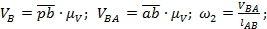

 ;
;

 ;
;
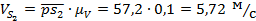 ;
;
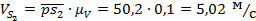 ;
;
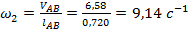 ;
;
 .
.
 , то
, то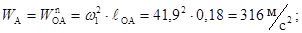
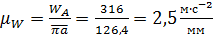 ;
; ;
;




 центра масс звена 2 находим по теореме подобия.
центра масс звена 2 находим по теореме подобия.