При растяжении брус удлиняется, а его поперечные размеры уменьшаются. Разность между длиной бруса после деформации ℓ1 и до деформации ℓ0 (рис.3.3) ∆ℓ = ℓ1- ℓ0 называется абсолютным удлинением. ∆ℓ>0 при растяжении и ∆ℓ<0 при сжатии. Экспериментально было установлено, что ∆ℓ =  . Эта зависимость называется законом Гука в деформациях. Здесь: А – площадь поперечного сечения бруса, ЕА - жесткость бруса при растяжении, сжатии, Е[
. Эта зависимость называется законом Гука в деформациях. Здесь: А – площадь поперечного сечения бруса, ЕА - жесткость бруса при растяжении, сжатии, Е[ 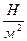 ] – упругая характеристика материала, называемая модулем упругости при растяжении. Его значения для некоторых материалов приведены в таблице
] – упругая характеристика материала, называемая модулем упругости при растяжении. Его значения для некоторых материалов приведены в таблице
.












| материал
| сталь
| медь
| алюминий
| титан
| дерево
|
|
Е, МПа
|
2∙105
|
1,1∙105
|
0,7∙105
|
1,2∙105
|
0,1∙105
|
Отношение ∆ℓ к первоначальной длине ℓ0 называется относительной продольной деформа-
цией, т.е.  . Разделим левую и правую части выражения закона Гука на первоначальную длину ℓ0:
. Разделим левую и правую части выражения закона Гука на первоначальную длину ℓ0: 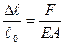 ,
,  т.к.
т.к.  ,
,  , то σ = Еε – это выражение называется законом Гука в напряжениях, из которого следует, что нормальные напряжения прямо пропорциональны относительному удлинению.
, то σ = Еε – это выражение называется законом Гука в напряжениях, из которого следует, что нормальные напряжения прямо пропорциональны относительному удлинению.
Абсолютная поперечная деформация бруса ∆b = b0 – b1 - это разность между поперечными размерами до и после нагружения:. Отношение  называется относительной поперечной деформацией. Между продольными и поперечными деформациями экспериментально установлена зависимость εпоп = -μεпрод, называемая законом Пуассона. Здесь εпрод - относительная продольная деформация, μ – коэффициент Пуассона, который так же является упругой характеристикой материала. Для металлов величина μ находится в пределах 0,25 -0,33. Наименьшее значение имеет пробка (μ=0), наибольшее – каучук(0,47).
называется относительной поперечной деформацией. Между продольными и поперечными деформациями экспериментально установлена зависимость εпоп = -μεпрод, называемая законом Пуассона. Здесь εпрод - относительная продольная деформация, μ – коэффициент Пуассона, который так же является упругой характеристикой материала. Для металлов величина μ находится в пределах 0,25 -0,33. Наименьшее значение имеет пробка (μ=0), наибольшее – каучук(0,47).













 . Эта зависимость называется законом Гука в деформациях. Здесь: А – площадь поперечного сечения бруса, ЕА - жесткость бруса при растяжении, сжатии, Е[
. Эта зависимость называется законом Гука в деформациях. Здесь: А – площадь поперечного сечения бруса, ЕА - жесткость бруса при растяжении, сжатии, Е[ 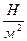 ] – упругая характеристика материала, называемая модулем упругости при растяжении. Его значения для некоторых материалов приведены в таблице
] – упругая характеристика материала, называемая модулем упругости при растяжении. Его значения для некоторых материалов приведены в таблице
 . Разделим левую и правую части выражения закона Гука на первоначальную длину ℓ0:
. Разделим левую и правую части выражения закона Гука на первоначальную длину ℓ0: 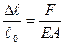 ,
,  т.к.
т.к.  ,
,  , то σ = Еε – это выражение называется законом Гука в напряжениях, из которого следует, что нормальные напряжения прямо пропорциональны относительному удлинению.
, то σ = Еε – это выражение называется законом Гука в напряжениях, из которого следует, что нормальные напряжения прямо пропорциональны относительному удлинению. называется относительной поперечной деформацией. Между продольными и поперечными деформациями экспериментально установлена зависимость εпоп = -μεпрод, называемая законом Пуассона. Здесь εпрод - относительная продольная деформация, μ – коэффициент Пуассона, который так же является упругой характеристикой материала. Для металлов величина μ находится в пределах 0,25 -0,33. Наименьшее значение имеет пробка (μ=0), наибольшее – каучук(0,47).
называется относительной поперечной деформацией. Между продольными и поперечными деформациями экспериментально установлена зависимость εпоп = -μεпрод, называемая законом Пуассона. Здесь εпрод - относительная продольная деформация, μ – коэффициент Пуассона, который так же является упругой характеристикой материала. Для металлов величина μ находится в пределах 0,25 -0,33. Наименьшее значение имеет пробка (μ=0), наибольшее – каучук(0,47).


