Закон парности касательных напряжений. Главные площадки, главные напряжения.
Касательные напряжения связаны между собой определенной зависимостью, которая следует из условий равновесия параллелепипеда (рис. 4.2): Эти соотношения носят название закона парности касательных напряжений: касательные напряжения по двум взаимно перпендикулярным площадкам равны по абсолютной величине и противоположны по знаку, т.е. касательные напряжения на двух взаимно перпендикулярных площадках направлены либо к линии пересечения этих площадок, либо от нее. Таким образом, на гранях выделенного элемента имеем не девять, а только шесть независимых компонентов напряжений: sx, sy, sz, txy, tyz, tzx.
 При изменении ориентации граней выделенного параллелепипеда меняются и напряжения, действующие на его гранях. При этом, как доказывается в теории упругости, можно провести такие три взаимно перпендикулярных площадки, на которых касательные напряжения будут отсутствовать.
Главные напряжения обозначаются s1, s2, s3, при расстановке индексов следует выполнять соотношение s1 ³ s2 ³ s3. Это неравенство следует понимать в алгебраическом смысле. Пусть одно из главных напряжений равно нулю, другое растягивающее – 40 МПа, третье сжимающее – 140 МПа, тогда
|
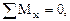
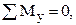
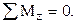Рассмотри первое уравнение равновесия: 
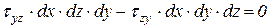. Из него следует 
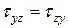. Аналогично из уравнений 
получим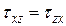 
, 
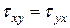. Таким образом 
, 
, 
.
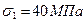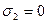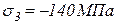