Прямая задача

Аналитическое решение прямой задачи определяется формулами (4.6) – (4.9).

Для графического решения строится на плоскости в координатах s-t круг Мора

(рис. 4.9) в следующей последовательности.

Рис. 4.9

Выбирается прямоугольная система координат так, чтобы ось абсцисс была параллельна большему из главных напряжений s₁, по этой оси в выбранном масштабе откладывются отрезки ОА и ОВ, численно равные напряжениям s₁ и s₂, а на их разности (на отрезке АВ) как на диаметре проводим окружность с центром в точке С.

Из крайней левой точки (В) круга проводим луч, параллельный внешней нормали к рассматриваемой площадке, т.е. под углом a к оси s. Точка пересечения этого луча с окружностью (D_a) имеет своими координатами отрезки D_aK_a и OK_a, численно равные касательному t_a и нормальному s_a напряжениям, действующим на рассматриваемой площадке.

Из рис.4.9 следует: AC=BC=CD_α= , СК_α=СК_β =СD_αcos2α = cos2α

Точка D_b, лежащая на противоположном конце диаметра от точки D_a, характеризует напряжения s_β и t_b, действующие по наклонной площадке, перпендикулярной к первой.

Выполненные преобразования проведены с учетом, что 1+cos2α = 2cos²α., 1-cos2α = 2sin²α.

Полученные выражения для s_a, s_b, τ_α и τ_β полностью совпадают с аналитическими формулами (4.6) - (4.9).

В заключение следует отметить, что каждая точка круга Мора имеет своими координатами напряжения, действующие на соответствующей площадке, следовательно, зная главные напряжения для плоского напряженного состояния, можно с помощью круга Мора определить напряжения, действующие на различных площадках, проходящих через данную точку. Максимальное касательное напряжение соответствует точке D_c и равно радиусу круга .
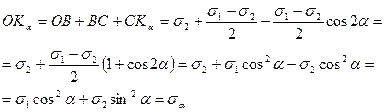