Обобщенный закон Гука
Рассматривая вопросы прочности при объемном и плоском напряженных состояниях, необходимо в соответствии с основными гипотезами считать, что материал изотропный, следует закону Гука, а деформации малы. Изучая центральное растяжение, сжатие, было установлено, что относительные продольная и поперечная деформации определяются выражениями
Эти равенства выражают закон Гука при простом растяжении или сжатии, т.е. при линейном напряженном состоянии (рис. 4.14).
 , где , где  , ,  , ,  - относительные удлинения в - относительные удлинения в
направлении s1, вызванные соответственно действием только Рис. 4.15
напряжениями s1, s2, s3. Поскольку
Складывая эти величины, получим Аналогично получаются выражения для двух других главных удлинений. В результате
Эти формулы носят название обобщенного закона Гука для изотропного тела, т. е. определяют зависимость между линейными деформациями и главными напряжениями в общем случае объемного напряженного состояния. Из этих формул легко получить закон Гука для плоского напряженного состояния. Например,
Выражения (4.14) справедливы не только для главных деформаций, но и для относительных деформаций по любым трем взаимно перпендикулярным направлениям. При выводе аналитического выражения обобщенного закона Гука в этом случае будем исходить из условия, что угловые деформации не зависят от нормальных напряжения, а ли-нейные деформации не зависят от касательных напряжений. В этом случае относительное удлинение по направлению оси х будет обусловлено напряжением σх и равно Таким образом,
Угловые деформации определяются соответствующими касательными напряжениями
Совокупность деформаций, возникающих по различн ым направлениям и в различных плоскостях, проходящих через данную точку, называется деформированным состоянием в точке. Наряду с линейной и угловой деформацией в сопротивлении материалов приходится рассматривать иногда и объёмную деформацию, т.е., относительное изменение объема в точке. Линейные размеры ребер элементарного параллелепипеда
Раскрывая скобки и пренебрегая произведениями линейных деформаций, как величинами второго порядка малости, получим Относительное изменение объёма обозначается буквой е и определится из отношения е Заменив деформации их выражениями по закону Гука, получим e Это соотношение на ряду с формулами (4.14)-(4.16) относится к обобщенному закону Гука.
4.8 П отенциальная энергия деформации
|

 ,
,  (4.12)
(4.12) Рассмотрим зависимость между напряжениями и деформациями в случае объемного напряженного состояния.
Рассмотрим зависимость между напряжениями и деформациями в случае объемного напряженного состояния.
 ,
, 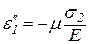 ,
,  . (4.13)
. (4.13) .
.
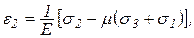 (4.14)
(4.14) .
. :
:


 . Напряжениям
. Напряжениям  в этом направлении будут соответствовать удлинения
в этом направлении будут соответствовать удлинения  и
и  .По аналогии получим такие же выражения для
.По аналогии получим такие же выражения для  и
и  .
.
 (4.15)
(4.15) .
.

 (4.16)
(4.16) в результате деформации меняются и становятся равными
в результате деформации меняются и становятся равными  . Абсолютное приращение объёма определится разностью
. Абсолютное приращение объёма определится разностью
 -
-  .
. .
.
 .
. (4.17)
(4.17)


