Напряжения sa и ta, действующие на площадке a, вызываются действием как напряжения s1, так и напряжения s2. Применяя принцип суперпозиции, получим выражения
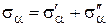 , , 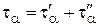 ,
где ,
где  - напряжения, вызванные действием s1, - напряжения, вызванные действием s1,
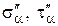 - напряжения, вызванные действием s2.
Согласно уравнениям (4.1), (4.2) - напряжения, вызванные действием s2.
Согласно уравнениям (4.1), (4.2)
 , , 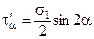 Для определения
Для определения  и и 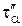 следует учесть, что нормаль na образует с направлением s2 угол b = 90 – a. Согласно правилам знаков для углов, он будет отрицательным. Тогда следует учесть, что нормаль na образует с направлением s2 угол b = 90 – a. Согласно правилам знаков для углов, он будет отрицательным. Тогда 
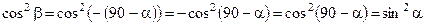
| |
Пусть по боковым граням элементарного параллелепипеда действуют главные напряжения s
1 и s
2. Определим напряжения на произвольной наклонной площадке, расположенной под углом a к главной (рис. 4. 8).


С учетом этих преобразований  ,
, 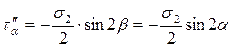 .
.
Тогда 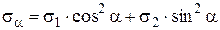 (4.6)
(4.6)
 (4.7)
(4.7)
Напряжения на площадке, перпендикулярной к рассмотренной, найдем по формулам (4.3), (4.4) учитывая, что угол между напряжением σ1 и нормалью nβ равен 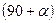 , а между
, а между
напряжением σ2 и этой же нормалью – α.
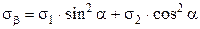 (4.8)
(4.8)
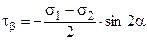 (4.9)
(4.9)
При сложении выражений (4.6) и (4.8) подтверждается положение, что сумма нормальных напряжений на взаимно перпендикулярных площадках – величина постоянная,
т. е. 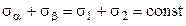 .
.
Для определения наибольшего и наименьшего значения нормального напряжения вычислим первую производную от sa по a выражения (4.6) и приравняем ее к нулю:
 . (4.10)
. (4.10)
Уравнение (4.10) удовлетворяется при a=0° и a=90°. Согласно (4.6)  при a=0°, а при a=90°
при a=0°, а при a=90° 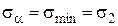 . В обоих этих случаях ta=0, следовательно, нормальные напряжения s1 и s2 принимают экстремальные значения на главных площадках.
. В обоих этих случаях ta=0, следовательно, нормальные напряжения s1 и s2 принимают экстремальные значения на главных площадках.
Наибольшее значение касательных напряжений, как следует из формулы (4.7), будут при a = 45°, т.е.,: 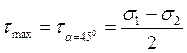 (4.11)
(4.11)



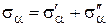 ,
, 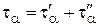 ,
где
,
где  - напряжения, вызванные действием s1,
- напряжения, вызванные действием s1,
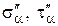 - напряжения, вызванные действием s2.
Согласно уравнениям (4.1), (4.2)
- напряжения, вызванные действием s2.
Согласно уравнениям (4.1), (4.2)
 ,
, 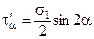 Для определения
Для определения  и
и 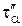 следует учесть, что нормаль na образует с направлением s2 угол b = 90 – a. Согласно правилам знаков для углов, он будет отрицательным. Тогда
следует учесть, что нормаль na образует с направлением s2 угол b = 90 – a. Согласно правилам знаков для углов, он будет отрицательным. Тогда 
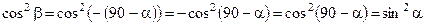

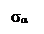
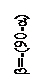

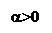
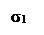
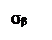

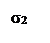
 ,
, 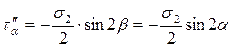 .
.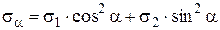 (4.6)
(4.6) (4.7)
(4.7)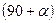 , а между
, а между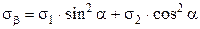 (4.8)
(4.8)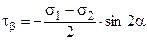 (4.9)
(4.9)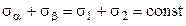 .
. . (4.10)
. (4.10) при a=0°, а при a=90°
при a=0°, а при a=90° 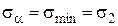 . В обоих этих случаях ta=0, следовательно, нормальные напряжения s1 и s2 принимают экстремальные значения на главных площадках.
. В обоих этих случаях ta=0, следовательно, нормальные напряжения s1 и s2 принимают экстремальные значения на главных площадках.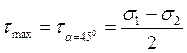 (4.11)
(4.11)


