Теории предельных напряженных состояний
Задачей теорий предельных напряженных состояний является оценка прочности детали при известном напряженном состоянии в её опасной точке. Эта задача решается просто при простых деформациях, в частности для одноосного напряженного состояния, так как в этом случае значения предельных (опасных) напряжений достаточно просто установить опытным путем. Предельное (опасное) напряженное состояние наступает, когда напряжения в детали достигают значений, соответствующих началу разрушения (при хрупком состоянии материала) или появлению остаточных деформаций (в случае пластичес-кого состояния материала). Испытание образцов из данного материала при одноосном растяжении или сжатии позволяет легко установить значения опасных напряжений(σ0 ): предел прочности для хрупких и предел текучести для пластических материалов, т.е., σ0= σв, или σ0= σт. А условие прочности в любой точке детали при линейном напряженном состоянии примет вид
Если в точках детали два или все три главных напряжений σ1, σ2, σ3 отличны от нуля, то в этих случаях, как показывают опыты, для одного и того же материала опасное состояние может наступить при различных предельных значениях главных напряжений Другой путь решения этой задачи заключается в выборе критериев прочности (критериев предельного напряженного состояния). В этом случае вводится гипотеза о преимущественном влиянии на прочность какого-то определенного фактора, полагая, что нарушение прочности материала при любом напряженном состоянии возможно тогда, когда этот фактор достигает своего предельного значения, величина которого может быть определена на основании простых опытов на растяжение. Такой подход позволяет сопоставить сложное напряженное состояние с линейным напряженным состоянием и установить эквивалентное (расчетное) напряжение, обеспечивающее в обеих случаях одинаковый коэффициент запаса. Выбранные рассмотренным образом критерии прочности часто называют теориями прочности. Рассмотрим некоторые из этих теорий. Первая теория прочности – теория наибольших нормальных напряжений была предложена в1638 году Галилео Галилеем. Согласно этой теории нарушение прочности в общем случае сложного напряженного состояния наступает, когда наибольшее нормальное напряжение достигает своего предельного значения σ0. В этом случае условие прочности будет следующим: σ1 Таким образом, первая теория прочности из трёх главных напряжений учитывает толь-ко одно наибольшее, считая, что два других на прочность не влияют. Опыты показали, что эта теория дает удовлетворительные результаты только для весь-ма хрупких материалов. Вторая теория прочности – теория наибольших линейных деформаций была предложена в1686 году Бойли Мариоттом. Согласно этой теории нарушение прочности в общем случае сложного напряженного состояния наступает, когда наибольшая линейная деформация достигает своего предельного значения ε0, которое определяется при простом растяжении, сжатии. Таким образом, разрушение наступает при Так как
При простом растяжении После подстановки (5.2), (5.3) в условие прочности (5.1) получим
Опытная проверка этой теории показала, что она, как и первая теория, дает удовлетворительные результаты лишь для весьма хрупких материалов. Третья теория прочности – теория наибольших касательных напряжений была предложена в 1773 году Кулоном. В этой теории в качестве критерия прочности принята величина наибольшего касательного напряжения, а нарушение прочности в общем случае сложного напряженного состояния наступает, когда наибольшие касательные напряжения достигают своего предельного значения τ0, т.е., разрушение наступает при Условие прочности - Так как
Эта теория прочности хорошо подтверждается экспериментально для материалов, одинаково работающих на растяжение и сжатие. Её недостатком является то, что она не учитывает влияния на прочность материала среднего по величине главного напряжения σ2 Если материал не одинаково сопротивляется растяжению, сжатию, то Мор предложил следующее условие прочности, называемое теорией Мора
где Использование этой теории затруднено, так как не для всех материалов есть данные для определения коэффициента «k». Четвёртая теория прочности – теория октаэдрических касательных напряжений (энергетическая теория прочности), предложенная Губертом в1904 году. Условие прочности с указанным критерием
Левая часть этого выражения определяется известной формулой
Для правой части при одноосном растяжении σ1= σ, σ2= σ3=0, тогда
После подстановки (5.10), (5.11) в выражение (5.9) получим формулу, определяющую условие прочности по четвертой теории предельного напряженного состояния. σэквIV= Контрольные вопросы
ИЗГИБ Основные понятия об изгибе Прямой брус испытывает деформацию изгиба, если он нагружен силами или парами сил в плоскости, проходящей через ось бруса, а сами силы или пары сил действуют перпен-дикулярно этой оси (рис. 5.1). Брус под действием этих сил изогнётся, его ось искривится, а в поперечных сечениях появятся изгибающий момент М и поперечная сила Q.

Брус испытывает прямой изгиб, если плоскость действия моментов совпадает с одной из главных плоскостей жёсткости. Главные плоскости жёсткости – это плоскости, проходящие через ось бруса и одну из главных центральных осей инерции (YOZ – плоскость максималь-ной жёсткости, XOZ– плоскость минимальной жёсткости). Если плоскость действия момента и плоскость перемещений (деформаций) совпадают, то такой изгиб называется плоским. Если изгибающий момент в поперечном сечении бруса является единственным силовым фактором, то такой изгиб называется чистым. Если наряду с изгибающим моментом в поперечном сечении бруса действует и поперечная сила, то изгиб называется поперечным. Прямолинейный брус, работающий на изгиб, называется балкой.
|

 , где
, где  =
=  ,
,  =
=  .
. , т.е., предельное состояние будет зависеть не только от значений главных напряжений, но и от соотношений между ними. Экспериментально установить предельные значения главных напряжений очень сложно не только из-за большого количества опытов, но и из-за технических порой непреодолимых трудностей.
, т.е., предельное состояние будет зависеть не только от значений главных напряжений, но и от соотношений между ними. Экспериментально установить предельные значения главных напряжений очень сложно не только из-за большого количества опытов, но и из-за технических порой непреодолимых трудностей. или
или  для материалов одинаково работающих на растяжение, сжатие; σ1
для материалов одинаково работающих на растяжение, сжатие; σ1  . А условие прочности будет следующим:
. А условие прочности будет следующим:  (5.1)
(5.1) может принимать значения равные
может принимать значения равные  или
или  , то левая часть условия прочности (5.1) может быть записана с использованием обобщенного закона Гука
, то левая часть условия прочности (5.1) может быть записана с использованием обобщенного закона Гука или
или  . (5.2)
. (5.2) (5.3)
(5.3)

 (5.4)
(5.4)

 . Предельное значение τ0 определяется при простом растяжении.
. Предельное значение τ0 определяется при простом растяжении. . (5.6)
. (5.6) , а для одноосного растяжения
, а для одноосного растяжения  , то из равенства (5.6) следует условие прочности по третьей теории
, то из равенства (5.6) следует условие прочности по третьей теории (5.7)
(5.7) , (5.8)
, (5.8)
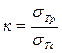 для пластических,
для пластических,  для хрупких материалов, а σТр, σТс, σвр, σвс пределы текучести и пределы прочности материала при растяжении и сжатии,
для хрупких материалов, а σТр, σТс, σвр, σвс пределы текучести и пределы прочности материала при растяжении и сжатии, IY (5.9)
IY (5.9) (5.10)
(5.10) ,
,  IY
IY  (5.11)
(5.11) (5.12)
(5.12) (альфа), аналитическим способом при плоском напряжённом состоянии?
(альфа), аналитическим способом при плоском напряжённом состоянии?


