Нормальные напряжения при чистом изгибе
  
 
                          
                  
       
   
 

центральные. Чтобы согласовать знак нормальных напряжений со знаком изгибающего момента ось У направлена вниз. Запишем уравнения равновесия левой части рассматриваемой балки (рис.6.16, б). ΣΧ=0 (6.1), ΣУ=0 (6.2), ΣZ= Уравнения (6.1), (6.2), (6.6) выполняются тождественно. Оставшиеся уравнения (6.3), (6.4), (6.5) имеют бесчисленное множество решений, т.к. они могут удовлетворятся при различных законах распределения нормальных напряжений по сечению. Таким образом, определение этих напряжений является статически неопределимой задачей. Для её решения рассмотрим закономернои деформаций при изгибе на примере бруса с прямоугольным сечением, которые при чистом изгибе легко обнаружить экспериментальным путём
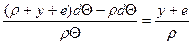 , т.е. , т.е.
ε Здесь
Это выражение представляет уравнение совместности деформаций, полученное на основе гипотезы плоских сечений и линейного напряженного состояния в поперечном сечении балки. Теперь уравнения равновесия (6.3), (6.4), (6.5) с учетом формулы (6.7) будут иметь единственное решение.
Уравнение (6.4):
Подставив значение кривизны (6.9) в уравнение (6.8), получим Максимальные напряжения будут при у = уmax, т.е., Из этого условия прочности может быть решен вопрос о размерах поперечного сечения балки
При поперечном изгибе в сечении бруса кроме изгибающего момента действует и поперечная сила. Следовательно, в этом случае в поперечных сечениях бруса возникают не только нормальные, но и касательные напряжения. Теоретические и экспериментальные исследования показывают, что формула нормальных напряжений при чистом изгибе применима и для поперечного изгиба, если отношение длины балки к её высоте ℓ/h >5.

параллельной оси балки, также будут действовать касательные напряжения согласно закону парности касательных напряжений. Составим уравнение равновесия рассматриваемого элемента, спроектировав все силы на ось балки Z: - N - dT + N + dN = 0 или dT = dN, здесь С учётом формулы где Так как
Выведенная формула впервые была получена Д.И.Журавским и носит его имя, из неё следует, что знак касательных напряжений определяется знаком силы Q, а их величина по высоте сечения меняется по параболическому закону и достигает наибольшей величины на нейтральной оси. Для прямоугольного сечения Ix=
Из этой формулы видно, что касательные напряжения по высоте меняются по закону квадратичной параболы. При у = На рис.6.21 показаны эпюры касательных напряжений для прямоугольного и круглого, на рис.6.22 для коробчатого и таврового сечений.


6.7 Расчёт балок на прочность по допускаемым напряжениям Из полученных формул для напряжений при поперечном изгибе

Первая опасная точка на поверхности балки, в ней линейное напряженное состояние, для которого условие прочности записывается для сечения, где М=|М|наиб
Вторая опасная точка рассматривается на нейтральной оси. В ней деформация чистого сдвига. Условие прочности записывается для сечения, где Q=|Q|наиб При чистом сдвиге σ1=τ, σ3=-τ. Используя четвертую теорию прочности, получим σэкв I v = Третья опасная точка берется в промежутке между поверхностью и нейтральной осью. Так как в этой точке плоское напряженное состояние, главные напряжения найдутся по известным формулам:
по третьей теории σэквIII = по четвертой - σэкв I v = Сечение, где располагается эта точка не столь определенно. Для его выбора, строго говоря, следует функцию
|


 =N =0 (6.3), ΣMх=
=N =0 (6.3), ΣMх=  =М (6.4), Mу=
=М (6.4), Mу=  =0 (6.5), ΣMz= 0 (6.6).
=0 (6.5), ΣMz= 0 (6.6). Поперечные сечения плоские и перпендикулярные к оси до деформации, остаются плоскими и перпендикулярными к оси балки после деформации. Часть волокон растягивается, часть сжимается. Между ними имеются волокна, которые не изменяют своей длины, они образуют нейтральный слой (рис.6.17). Линия пересечения нейтрального слоя с поперечным сечением называется нейтральной линией.
Поперечные сечения плоские и перпендикулярные к оси до деформации, остаются плоскими и перпендикулярными к оси балки после деформации. Часть волокон растягивается, часть сжимается. Между ними имеются волокна, которые не изменяют своей длины, они образуют нейтральный слой (рис.6.17). Линия пересечения нейтрального слоя с поперечным сечением называется нейтральной линией. .
. -расстояние нейтрального слоя от центральной оси х.
-расстояние нейтрального слоя от центральной оси х. По закону Гука для одноосного растяжения
По закону Гука для одноосного растяжения  (6.7).
(6.7). ,
,  ≠0, следовательно,
≠0, следовательно, 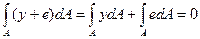 . Каждый из последних двух интегралов должен равняться нулю. Первый интеграл представляет статический момент площади
. Каждый из последних двух интегралов должен равняться нулю. Первый интеграл представляет статический момент площади  так как он равен нулю, то нейтральная линия совпадает с центральной осью Х, во втором интеграле
так как он равен нулю, то нейтральная линия совпадает с центральной осью Х, во втором интеграле  А≠0,следовательно,
А≠0,следовательно,  , т.е., нейтральный слой проходит через ось бруса. В этом случае
, т.е., нейтральный слой проходит через ось бруса. В этом случае  (6.8).
(6.8). ,
, 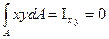 . Центробежный момент инерции равен нулю, поэтому оси Х,У являются главными центральными.
. Центробежный момент инерции равен нулю, поэтому оси Х,У являются главными центральными. так как
так как  , то
, то  (6.9),
(6.9), - кривизна изогнутой оси балки.
- кривизна изогнутой оси балки.  - жёсткость при изгибе.
- жёсткость при изгибе. (6.10). Это формула для нормальных напряжений при чистом изгибе. Из неё следует, что по ширине сечения нормальные напряжения не меняются, а по высоте (вдоль оси У) они меняются по линейному закону (рис.6.19).
(6.10). Это формула для нормальных напряжений при чистом изгибе. Из неё следует, что по ширине сечения нормальные напряжения не меняются, а по высоте (вдоль оси У) они меняются по линейному закону (рис.6.19). 
 но
но  - момент сопротивления изгибу, тогда
- момент сопротивления изгибу, тогда  . Эта формула позволяет записать условие прочности при изгибе по нормальным напряжениям при условии, что материал одинаково сопротивляется растяжению, сжатию:
. Эта формула позволяет записать условие прочности при изгибе по нормальным напряжениям при условии, что материал одинаково сопротивляется растяжению, сжатию:  ≤ [σ]. (6.11)
≤ [σ]. (6.11) ≥
≥  (6.12) и о её грузоподъёмности
(6.12) и о её грузоподъёмности  (6.13)
(6.13) 6.6.2 Напряжения при поперечном изгибе
6.6.2 Напряжения при поперечном изгибе

 .
В элементарной теории изгиба принимается, что касательные напряжения по ширине се-чения b(y) остаются постоянными, изменяя-ются лишь по высоте. В плоскости сечения,
.
В элементарной теории изгиба принимается, что касательные напряжения по ширине се-чения b(y) остаются постоянными, изменяя-ются лишь по высоте. В плоскости сечения,
 , N=
, N=  .
. выражение нормальной силы примет вид: N=
выражение нормальной силы примет вид: N=  ,
, , тогда N=
, тогда N= 
 , dN=
, dN=  =
=  , откуда следует
, откуда следует  .
. , то окончательно получим
, то окончательно получим . (6.13)
. (6.13)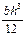 ,
,  ,
, .
.
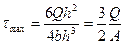 .
. следует: в точках на поверхности балки σ=|σ|наиб, τ=0; в точках на нейтральной оси τ=|τ|наиб, σ =0; в промежутке между этими точками и нормальные и касательные напряжения отличны от нуля. Таким образом, при расчетах на прочность при изгибе по допускаемым напряжениям следует рассматривать несколько опасных точек(рис.6.23).
следует: в точках на поверхности балки σ=|σ|наиб, τ=0; в точках на нейтральной оси τ=|τ|наиб, σ =0; в промежутке между этими точками и нормальные и касательные напряжения отличны от нуля. Таким образом, при расчетах на прочность при изгибе по допускаемым напряжениям следует рассматривать несколько опасных точек(рис.6.23). .
. .
. =
=  , или
, или  .
.
 . С учетом этих выражений запишем условия прочности:
. С учетом этих выражений запишем условия прочности: =
=  ,
, =
=  исследовать на экстремум. Обычно таким сечением является сечение, где Q и М достаточно велики.
исследовать на экстремум. Обычно таким сечением является сечение, где Q и М достаточно велики.


