Главных центральных осей
Главные центральные моменты инерции аналитическим способом вычислим по формуле
=
Положение главных центральных осей определим по формуле
Отложив угол α0 = - 42,40 по часовой стрелке от центральной оси Х, получим направление главной центральной оси х0, перпендикулярно ей проведем главную центральную ось у0. Контрольные вопросы 1. Что относится к геометрическим характеристикам поперечного сечения бруса, используемых в сопротивлении материалов? 2. Как определяются статические моменты площади поперечного сечения бруса? 3. Как определяются статические моменты площади поперечного сечения бруса, если известны площадь и координаты её центра тяжести? 4. Как определяются осевые моменты инерции поперечного сечения бруса? 5. Формулы осевых моментов инерции прямоугольника? 6. Формулы осевых моментов инерции круга? 7. Формулы осевых моментов инерции кольца. 8. Как определяется полярный момент инерции поперечного сечения бруса? 9. Как определяется центробежный момент инерции поперечного бруса? 10. Что называется моментом сопротивления сечения изгибу? 11. Формулы моментов сопротивления сечения изгибу прямоугольника, круга, кольца? 12. Что называется полярным моментом сопротивления сечения? 13. Формулы полярных моментов сопротивления круглого и кольцевого сечений. 14. Какие оси называются центральными? 15. Чему равны статические моменты площади сечения относительно центральных осей? 16. Какие оси называются главными? 17. Какие оси называются главными центральными? 18. Формулы преобразования моментов инерции при параллельном переносе осей? 19. Формулы преобразования моментов инерции при повороте от главных центральных осей? 20. Формулы для вычисления главных центральных моментов инерции? 21. Формула для определения положения главных центральных осей? 22. Порядок вычисления геометрических характеристик сложных сечений?
|

 =
= 

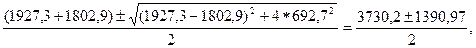
 см4,
см4, см4
см4



