Равенство нулю равнодействующей – необходимое и достаточное условие равновесия системы сходящихся сил.
Соответственно двум способам определения равнодействующей условие равновесия плоской системы сходящихся сил может быть выражено в двух формах. 1) Условие равновесия в геометрической форме. Геометрически равнодействующая сходящихся сил определяется как замыкающая сторона силового многоугольника, построенного на этих силах. Если равнодействующая равна нулю, то нужно, чтобы равнялась нулю и замыкающая сторона и, следовательно, силовой многоугольник замыкался сам по себе. С другой стороны, замыкание силового многоугольника означает, что равнодействующая сходящихся сил равна нулю. Отсюда получается следующее условие: для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный для этой системы сил, был замкнут.
2) Условие равновесия в аналитической форме. Условием равновесия системы сходящихся сил является равенство нулю модуля равнодействующей (
Таким образом, для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы порознь равнялись нулю суммы проекций всех сил на каждую из двух любых взаимно перпендикулярных осей, лежащих в плоскости действия сил. 1.2.5. Разложить силу на составляющие – это значит найти такую систему двух или нескольких сил, которая бы производила на тело то же самое действие, что и одна данная сила. Другими словами, разложить силу, например, на две составляющие – это значит найти такие две силы, равнодействующая которых была бы равна данной силе. Решений у такой задачи может быть сколько угодно много. Чтобы решение было определённым, необходимо задать дополнительные условия, например: 1) задание двух направлений, по которым должны действовать составляющие; 2) задание модуля и направления одной из составляющих сил; 3) задание модуля обеих составляющих; 4) задание модуля одной составляющей силы и направления другой.
Для решения задачи из конца А вектора силы Вопросы для самопроверки.
1. Какая система сил называется сходящейся? 2. Что называется замыкающей стороной силового многоугольника? О чём свидетельствует равенство её нулю? 3. Сформулируйте условие равновесия плоской сходящейся системы сил в аналитичесой форме. 4. Достаточно ли данных, чтобы разложить заданную по величине и направлению силу на две составляющих, из которых одна задана по величине, а другая по направлению?
|

 На рис. 1.2.8. построен замкнутый силовой многоугольник для находящейся в равновесии плоской системы сил
На рис. 1.2.8. построен замкнутый силовой многоугольник для находящейся в равновесии плоской системы сил  . Необходимо заметить, что в замкнутом силовом многоугольнике конец вектора последней силы совпадает с началом вектора первой, а стрелки векторов всех сил указывают одну и ту же сторону обхода периметра многоугольника.
. Необходимо заметить, что в замкнутом силовом многоугольнике конец вектора последней силы совпадает с началом вектора первой, а стрелки векторов всех сил указывают одну и ту же сторону обхода периметра многоугольника.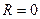 ), т. е. проекции (
), т. е. проекции (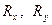 ) равнодействующей силы на оси координат (на каждую из двух любых взаимно перпендикулярных осей) должны быть равны нулю. Отсюда для плоской системы сходящихся сил получим два уравнения равновесия этих сил:
) равнодействующей силы на оси координат (на каждую из двух любых взаимно перпендикулярных осей) должны быть равны нулю. Отсюда для плоской системы сходящихся сил получим два уравнения равновесия этих сил: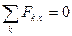 и
и  . (1.2.6.)
. (1.2.6.) Рассмотрим первый, наиболее часто встречающиеся, случай. Данную силу
Рассмотрим первый, наиболее часто встречающиеся, случай. Данную силу 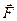 требуется разложить на две сходящиеся составляющие силы, направления которых ОМ и ON заданы (рис. 1.2.9.)
требуется разложить на две сходящиеся составляющие силы, направления которых ОМ и ON заданы (рис. 1.2.9.)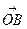 и
и  дают в том же масштабе, что и заданная сила
дают в том же масштабе, что и заданная сила  и
и 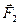 .
.


