Уравнение плоской и сферической волны.Возьмем волновую поверхность, отстоящую от начала координат на l. Колебания в ней будут отставать от начального на время
Уравнение плоской незатухающей волны в направлении волнового вектора:
Для затухающих волн надо добавить множитель:
Перейдем от радиус – вектора
(X)
Запись в комплексной форме:
|
:
- радиус – вектор произвольной точки;
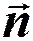- единичный вектор нормали к волнов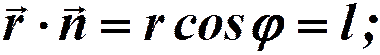ой поверхности.
- волновой вектор, нормаль к волновой поверхности.
тогда:
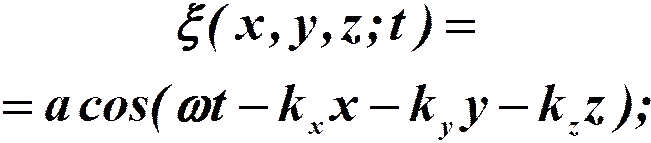
- комплексная амплитуда;
