Задача о назначении. 1. Розв’язати задачу про призначення за допомогою симплекс таблиці
1. Розв’язати задачу про призначення за допомогою симплекс таблиці 2. Розв’язати задачу про призначення за допомогою транспортної таблиці 3. Розв’язати задачу про призначення угорським методом 4. Розв’язати задачу комівояжера методом Літтла (метод гілок та границь) 5. Розв’язати задачу комівояжера угорським методом
Задача о назначении Имеется п видов работ, которые могут быть выполнены п кандидатами, где п – некоторое натуральное число. При этом каждого кандидата следует назначить на выполнение только одной работы, а каждая работа может выполняться только одним кандидатом. Заданы эффективности Введем в рассмотрение следующие булевы переменные: xij , которые будут соответствовать назначению кандидатов на выполнение работ. В этом случае резонно предположить, что xij = 1, если i - ый кандидат назначается на выполнение j -ой работы, и = xij = 0, если i - ый кандидат не назначается на выполнение j -ой работы Тогда математическая постановка задачи о назначении может быть сформулирована следующим образом.
где множество допустимых альтернатив
В математической постановке задачи о назначении первое ограничение соответствует требованию назначения каждого кандидата на выполнение только одной работы, а второе ограничение – требованию выполнения каждой работы только одним кандидатом. Нетрудно заметить, что общее число булевых переменных задачи о назначении равно: n2 . Классическая задача о назначении является симметричной, т. е. формулируется в форме, когда имеет место равенство общего числа работ и общего числа кандидатов. Если это условие не выполняется, то задача о назначении называется несимметричной. Однако при решении практических задач о назначении с помощью программы MS Excel данную особенность можно не принимать во внимание. Классическая задача о назначении формулируется как задача максимизации целевой функции, она достаточно просто может быть преобразована в эквивалентную задачу с минимизацией целевой функции. Для этого необходимо все значения сij умножить на -1, после чего полученные значения сложить с достаточно большим положительным числом, так чтобы все сij были положительными. Для решения задачи о назначении с помощью программы MS Excel необходимо задать конкретные значения параметрам. Для определенности рассмотрим вариант задачи о назначении в форме минимизации общих затрат на выполнение работ. В этом случае в качестве кандидатов рассмотрим сотрудников некоторой фирмы: Андреев, Бубнов, Васильев, Григорьев и Дмитриев, а в качестве работ – вакантные должности в этой фирме: менеджер, программист, бизнес-аналитик, маркетолог и руководитель проектов. Затраты
Соответствующая математическая постановка рассматриваемой задачи о назначении может быть записана в следующем виде: 5х11 + 10х12 + 9х13 +14x14 + 6х15 + 13х21 + 15х22 + 11х23 + 19х24 + 17х25 + + 7х31 +14х32 +12х33 + 8х34 +10х35 + 8х41 + 11х42 + 6х43 + 7х44 + 9 х45 + 15х51 +12х52 + 17х53 +13х54 + 16х55 где множество допустимых альтернатив
Заметим, что первые 5 ограничений данной задачи соответствуют общему ограничению (6.4.2), следующие 5 ограничений— общему ограниче: 4.3), а последнее ограничение — общему ограничению (6.4.4). 1ля решения сформулированной индивидуальной задачи о назначении с: елью программы MS Excel создадим в книге Булево программиров;)вый лист и изменим его имя на Задача о назначении. Для решения за; i полним следующие подготовительные действия: Знесем необходимые надписи в ячейки А7:А13, Bl, Gl, B7:G7, какизображено на рис.6. И. Следует отметить, что конкретное содерж;:-тих надписей не оказывает никакого влияния
|







 индивидуального выполнения каждым из потенциальных кандидатов всех рассматриваемых работ. Требуется распределить всех кандидатов по работам так, чтобы общая эффективность выполнения всех работ была наибольшей.
индивидуального выполнения каждым из потенциальных кандидатов всех рассматриваемых работ. Требуется распределить всех кандидатов по работам так, чтобы общая эффективность выполнения всех работ была наибольшей.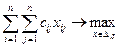
 формируется следующей стстемой ограничений типа неравенств:
формируется следующей стстемой ограничений типа неравенств:
 на замещение должностей кандидатами, связанные с необходимостью их предварительного обучения и стажировки, заданы в форме следующей таблицы:
на замещение должностей кандидатами, связанные с необходимостью их предварительного обучения и стажировки, заданы в форме следующей таблицы: ,
,



