Гармонические колебания. Гармоническиминазываются колебания, при которых изменения колеблющейся величины со временем происходят по закону синуса или косинуса
Г армоническими называются колебания, при которых изменения колеблющейся величины со временем происходят по закону синуса или косинуса. Гармонические колебания происходят под действием возвращающей силы Fвозв ., прямо пропорциональной смещению тела x и направленной к положению равновесия. Fвозв. = -k×x (3.1) Возвращающая сила подобна упругой, т.к. пропорциональна смещению и направлена к положению равновесия. Такие силы, неупругие по природе, но аналогичные по свойствам силам, возникающим при малых деформациях упругих тел, называются квазиупругими. Уравнение гармонических колебаний имеет вид:
Данное уравнение является решением дифференциального уравнения для собственных колебаний, о котором будет сказано позже. Основные кинематические характеристики гармонического колебания: Смещение x характеризует отклонение от положения равновесия в данный момент времени. Амплитуда A – максимальное смещение A= | xmax | Смещение и амплитуда в системе СИ измеряются в метрах. [ A ]=[ x ]=м Период T – время одного полного колебания. T=t/n (3.3), где t – время, за которое совершено n колебаний. Единица измерения периода колебаний – секунда,[ T ]=c Для математического маятника (материальная точка массой m, подвешенная на невесомой и нерастяжимой нити длиной l) период может быть найден из формулы:
При малых отклонениях от положения равновесия в поле силы тяжести эта система будет совершать (без учета сил сопротивления среды) свободные незатухающие колебания. Для пружинного маятника (материальная точка массой m, закрепленная на пружине с жесткостью k) период выражается формулой:
Частота колебаний n показывает число колебаний за единицу времени; является величиной, обратной периоду. n=n/t; n=1/T (3.6) Частота колебаний измеряется в герцах.[n]=Гц=с-1 Циклическая (круговая частота) w0 показывает число колебаний за 2 p сек. w0=2p n f=2p /T (3.7) Скорость V материальной точки, совершающей гармонические колебания, можно получить, дифференцируя выражение для координаты x по времени t:
Ускорение материальной точки при гармонических колебаниях можно получить, дифференцируя выражение для скорости по времени:
Фаза колебания j характеризует положение колеблющейся системы в любой момент времени, начальная фаза j0 – в начальный момент времени. С помощью начальной фазы учитывается различие между моментом начала отсчета времени (t =0) и моментом начала колебаний (x =0), если они не совпадают. j=j0+w0 ×× t (3.10) Зная фазу колебаний, можно определить, какая доля периода прошла от начала колебаний. Так фазе j=p /2 соответствует момент времени t=T /4; фазе j=p соответствует момент времени t=T /2. Фаза колебаний представляет собой аргумент тригонометрической функции и, следовательно, измеряется в радианах. Основные энергетические характеристики гармонического колебания. Используя полученное выражение для скорости, можно записать формулу для кинетической энергии
Формула для потенциальной энергии упругой деформации имеет вид: Подставив в данную формулу выражение для координаты x, можно вычислить потенциальную энергию колебательного движения:
Полная энергия колеблющейся материальной точки равна сумме кинетической и потенциальной энергий:
В процессе колебаний потенциальная энергия превращается в кинетическую энергию и наоборот. При этом полная энергия для незатухающих колебаний остается постоянной. Процесс перехода энергии из одного вида в другой носит периодический характер. В случае, когда присутствуют силы сопротивления среды, кинетическая энергия колеблющейся системы затрачивается на их преодоление, вследствие чего величина полной энергии постепенно уменьшается (случай затухающих колебаний).
|

 (3.2)
(3.2) (3.4)
(3.4) (3.5)
(3.5) (3.8)
(3.8) (3.9)
(3.9)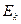 материальной точки, совершающей гармонические колебания:
материальной точки, совершающей гармонические колебания: (3.11)
(3.11)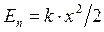 (3.12).
(3.12).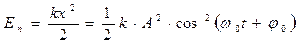 (3.13)
(3.13) (3.14)
(3.14)


