Динамика вращательного движения.

Основные понятия.

Момент силы относительно оси вращения – это векторное призведение радиус-вектора на силу.

(1.14)

Момент силы – это вектор,направление которого определяется по правилу буравчика (правого винта) в зависимости от направления силы, действующей на тело. Момент силы направлен вдоль оси вращения и не имеет конкретной точки приложения.

Численное значение данного вектора определяется по формуле:

M=r×F ×; sina (1.15),

где a - угол между радиус-вектором и направлением действия силы.

Если a=0 или p, момент силы М=0, т.е. сила, проходящяя через ось вращения или совпадающяя с ней, вращения не вызывает.

Наибольший по модулю вращающий момент создается, если сила действует под углом a=p/2 (М > 0) или a=3p/2 (М < 0).

Используя понятие плеча силы (плечо силы d – это перпендикуляр, опущенный из центра вращения на линию действия силы), формула момента силы принимает вид:

, где (1.16)

Правило моментов сил (условие равновесия тела, имеющего неподвижную ось вращения):

Для того, чтобы тело, имеющее неподвижную ось вращения, находилось в равновесии, необходимо, чтобы алгебраическая сумма моментов сил, действующих на данное тело, равнялась нулю.

S М_i =0 (1.17)

Единицей измерения момента силы в системе СИ является [Н×м]

При вращательном движении инертность тела зависит не только от его массы, но и от распределения ее в пространстве относительно оси вращения.

Инертность при вращении характеризуется моментом инерциитела относительно оси вращения J.

Момент инерции материальной точки относительно оси вращения – это величина, равная произведению массы точки на квадрат ее расстояния от оси вращения:

J_i=m_i× r_i² (1.18)

Моментом инерции тела относительно оси называется сумма моментов инерции материальных точек, из которых состоит тело:

J=S m_i× r_i² (1.19)

Момент инерции тела зависит от его массы и формы, а также от выбора оси вращения. Для определения момента инерции тела относительно некоторой оси используется теорема Штейнера-Гюйгенса:

J=J₀+m× d² (1.20),

где J₀ – момент инерции относительно параллельной оси, проходящей через цент масс тела, d – расстояние между двумя параллельными осями. Момент инерции в СИ измеряется в [кг×м²]

Момент инерции при вращательном движении туловища человека определяют опытным путем и рассчитывают приблизительно по формулам для цилиндра, круглого стержня или шара.

Момент инерции человека относительно вертикальной оси вращения, которая проходит через центр масс (центр масс тела человека находится в сагиттальной плоскости немного впереди второго крестцового позвонка), в зависимости от положения человека, имеет следующие значения: при стойке “смирно” – 1,2 кг×м²; при позе «арабеск» – 8 кг×м²; в горизонтальном положении – 17 кг ×;м².

Работа во вращательном движении совершается при вращении тела под действием внешних сил.

Элементарная работа силы во вращательном движении равна произведению момента силы на элементарный угол поворота тела:

dA_i=M_i× dj (1.21)

Если на тело действует несколько сил, то элементарная работа равнодействующей всех приложенных сил определяется по формуле:

dA=M× dj (1.22),

где М – суммарный момент всех внешних сил, действующих на тело.

Кинетическая энергия вращающегося тела W_к зависит от момента инерции тела и угловой скорости его вращения:

(1.23)

Момент импульса (момент количества движения) – величина, численно равная произведению импульса тела на радиус вращения.

L=p× r=m× V× r (1.24).

После соответствующих преобразований можно записать формулу для определения момента импульса в виде:

(1.25).

Момент импульса – вектор, направление которого определяется по правилу правого винта. Единицей измерения момента импульса в СИ является [кг×м²/с]

 

Основные законы динамики вращательного движения.

Основное уравнение динамики вращательного движения:

Угловое ускорение тела, совершающего вращательное движение, прямо пропорционально суммарному моменту всех внешних сил и обратно пропорционально моменту инерции тела.

(1.26).

Данное уравнение играет ту же роль при описании вращательного движения, что и второй закон Ньютона для поступательного движения. Из уравнения видно, что при действии внешних сил угловое ускорение тем больше, чем меньше момент инерции тела.

Второй закон Ньютона для динамики вращательного движения можно записать в ином виде:

(1.27),

т.е. первая производная от момента импульса тела по времени равна суммарному моменту всех внешних сил, действующих на данное тело.

Закон сохранения момента импульса тела:

Если суммарный момент всех внешних сил, действующих на тело, равен нулю, т.е.

S M_i =0, тогда dL/dt=0 (1.28).

 

Из этого следует или (1.29).

 

Это утверждение составляет сущность закона сохранения момента импульса тела, который формулируется следующим образом:

Момент импульса тела остается постоянным, если суммарный момент внешних сил, действующих на вращающееся тело, равен нулю.

Этот закон является справедливым не только для абсолютно твердого тела. Примером является фигурист, который выполняет вращение вокруг вертикальной оси. Прижимая руки, фигурист уменьшает момент инерции и увеличивает угловую скорость. Чтобы затормозить вращения, он, наоборот, широко разводит руки; в результате момент инерции увеличивается, и угловая скорость вращения уменьшается.

В заключение приведем сравнительную таблицу основных величин и законов, характеризующих динамику поступательного и вращательного движений.

 

Таблица 1.4.

 

Поступательное движение	Вращательное движение
Физическая величина	Формула	Физическая величина	Формула
Масса	m	Момент инерции	J=m×r2
Сила	F	Момент силы	M=F×r, если
Импульс тела (количество движения)	p=m×V	Момент импульса тела	L=m×V×r; L=J×w
Кинетическая энергия		Кинетическая энергия
Механическая работа	dA=FdS	Механическая работа	dA=Mdj
Основное уравнение динамики поступательного движения		Основное уравнение динамики вращательного движения	,
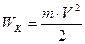
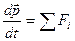
Закон сохранения импульса тела	или если	Закон сохранения момента импульса тела	или SJiwi=const, если