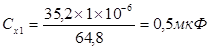Краткое теоретическое введение.

Лабораторная работа 2-02.

Тема: Определение ёмкости конденсаторов измерительным мостиком Соти.

Цель работы: измерение теплоёмкостей двух конденсаторов, проверка закона последовательного и параллельного соединения конденсаторов.

Приборы и принадлежности: осциллограф, звуковой генератор как источник переменного напряжения, конденсатор с известной ёмкостью, два конденсатора с неизвестными ёмкостями, реохорд, соединительные провода.

Для измерений теплоёмкостей используется классическая мостовая схема, называемая мостиком Соти. На рис.1 показана схема простейшего моста Соти.

		К
		M
	C1			C2
		N

Рис.1

A

B

l2

l1

Схема содержит конденсаторы С₁, С₂, омические сопротивления R_1, R₂, осциллограф и звуковой генератор ЗГ для питания схемы.

Пусть Δφ_1, Δφ₂ – мгновенные значения напряжений на обкладках конденсаторов, а

Δφ_AN, Δφ_NB – мгновенные значения напряжений на сопротивлениях R_1, R₂.

Δφ₁=U₁= φ_M- φ_A;

Δφ₂=U₂= φ_M- φ_B;

Обозначим φ_A,φ_B,φ_M,φ_N – мгновенные значения потенциалов в точках A, B, M, N, соответственно. Тогда

Δφ_AN= φ_A- φ_N;

Δφ_NB= φ_B- φ_N;

Так как потенциалы в точках M и N различны, в ветвях MAN, MBN, ATB текут переменные токи. При любых произвольных R₁ и R₂ напряжения Δφ_1, Δφ_2, Δφ_AN и Δφ_NB

отличаются друг от друга, но сопротивления R₁ и R₂ можно подобрать так, что ток в диагонали моста ВТА станет равен нулю. Это имеет место когда потенциалы точек А и В

окажутся одинаковыми. Тогда

Δφ₁= Δφ₂ ;

Δφ_AN= Δφ_BN.

Если ток в диагонали ВТА равен нулю, то ток i₁= Δφ_AN/R₁ заряжает конденсатор С₁, а ток i₁= Δφ_NВ/R₂ заряжает конденсатор С₂.

На обкладках конденсаторов за время Δt накапливаются заряды Δq₁ и Δq₂.

Δq₁= Δφ_AN/R₁ × Δt

Δq₂= Δφ_NВ/R₂× Δt

Электроёмкость проводника измеряется количеством электричества, которое необходимо сообщить проводнику, чтобы изменить его потенциал на единицу потенциала, следовательно, С= Δq / Δφ и поэтому электроёмкости первого и второго конденсаторов определяются соотношениями:

 

С₁= Δφ_AN/R₁ × Δt/ Δφ₁

С₂= Δφ_NВ/R₂× Δt/ Δφ₂

Следовательно:

С₁/С₂=R₂/R₁.

Сопротивления участков струны AN и NB соответственно равны R₁=ρ*l₁/s и

R₁=ρ*l₂/s,

где ρ-удельное сопротивление, s-сечение струны, l₁ и l₂ – длины участков струны AN и BN. Подвижный участок N скользит по струне и изменяет отношение плеч. При произвольном положении контакта N в диагонали моста ATB течёт ток и в телефоне слышен звук. Когда контакт приближается к положению, при котором ток, идущий через телефон, становится исчезающе мал, звук замирает. Если звук в телефоне исчез, то сопротивления R₁ и R₂ оказались такими, что выполняется соотношение:

 

левое плечо:

l C	l’ 1	l’’ 1	l’ ‘’1	l 1ср	l 2	Величина ёмкости, мкФ
Cx1	66.5	66.4	66.6	66.5	33.5	0,5
Cx2	46.6	46.8	46.2	46.5	53.5	0,8
Cx посл	73.4	73.3	73.5	73.4	26.6	0,4
Cx паралл	38.6	38.7	38.8	38.7	61.3	1,6

 

 

правое плечо:

l C	l’ 1	l’’ 1	l’ ‘’1	l 1ср	l 2	Величина ёмкости, мкФ
Cx1	35,1	35,2	35,3	35,2	64,8	0,5
Cx2	52,4	53,4	52,5	52,8	47,2	1,1
Cx посл		29,1	29,2	29,1	70,9	0,4
Cx паралл	61,4	61,5	61,3	61,4	38,6	1,6

 

 

Cx1 ср	Cx2 ср	Cx посл ср	Cx паралл ср
0,5 мкФ	0,95 мкФ	0,4 мкФ	1,6 мкФ

 

 

С_Э=1*10^-6мкФ

 

Подсчёт результатов:

Левое плечо:

Правое плечо:

 

Вывод:

С помощью мостовой схемы, называемой “мостиком Соти” мы измерили электроёмкости 2х конденсаторов, а также проверили законы последовательного и параллельного соединения конденсаторов. На основании данных таблиц нашли средние значения неизвестных ёмкостей C_x1 и C_x2 , а также ёмкости C_{x паралл} и C_{x посл} , которые образуются при последовательном и параллельном соединении конденсаторов.