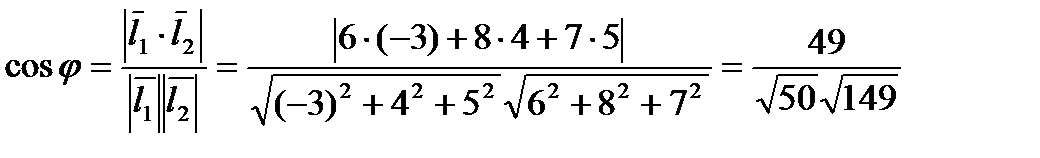АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.
Уравнения плоскости Пусть задан вектор
Рис.8 Вектор
Полученное уравнение – уравнение плоскости, проходящей через точку
Пример. Составить уравнение плоскости, проходящей через точку Решение. Пусть
Вектор
Рис.9
Рассмотрим плоскость, проходящую через три точки, не лежащие на одной прямой:
Рис.10 Три вектора:
лежат в одной плоскости, значит компланарны, и их смешанное произведение равно нулю: Запишем смешанное произведение в координатной форме, получим:
через три точки.
Пример. Найти уравнение плоскости, проходящей через три точки
Рис.11
Решение. Пусть точка Смешанное произведение векторов равно нулю:
Пусть плоскость Расстояние от точки
Рис.12
Пример. Найти расстояние от точки Решение. Воспользуемся формулой расстояния от точки до плоскости, получим:
Угол между плоскостями равен углу Пусть даны две плоскости: плоскость плоскость
Рис.13
Косинус угла между плоскостями вычисляется по формуле:
Пример. Найти угол между плоскостями
Решение. Векторы нормалей имеют координаты:
Уравнения прямой в пространстве
Рассмотрим в пространстве прямую a, проходящую через точку
Рис.14
Пусть точка Эти уравнения - канонические уравнения прямой в пространстве. Если в канонических уравнениях ввести параметр t:
Прямую можно задать как линию пересечения двух плоскостей (рис.15):
Рис.15
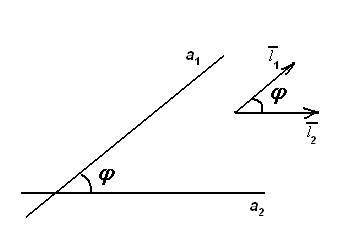
Уравнения прямой, проходящей через две точки Угол между прямыми равен острому углу между их направляющими векторами (рис.16) и вычисляется по формуле:
Рис.16
Пример. Прямая
а) Написать для этой прямой канонические и параметрические уравнения; б) Найти угол между прямой
Решение. а)Выберем одну из точек, через которую пройдет указанная прямая, заданная пересечением плоскостей. Исходная система имеет бесчисленное множество решений, одно из которых получим придавая одной из переменных конкретное значение. Пусть Решением этой системы является пара чисел В результате получим точку
Запишем канонические уравнения прямой Получим из канонических параметрические уравнения прямой: б) Направляющий вектор прямой
|


 , перпендикулярный к плоскости
, перпендикулярный к плоскости  (вектор нормали) и точка
(вектор нормали) и точка 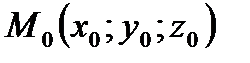 - произвольная фиксированная точка плоскости. Возьмем на плоскости
- произвольная фиксированная точка плоскости. Возьмем на плоскости  произвольную нефиксированную точку
произвольную нефиксированную точку  - (текущая точка) (рис.8).
- (текущая точка) (рис.8).
 , лежащий в плоскости
, лежащий в плоскости  , перпендикулярен вектору нормали
, перпендикулярен вектору нормали 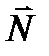 , значит их скалярное произведение
, значит их скалярное произведение  , следовательно
, следовательно
 , перпендикулярно вектору
, перпендикулярно вектору  .
. и перпендикулярно вектору
и перпендикулярно вектору 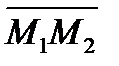 , если
, если  ,
, 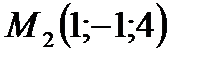 (рис.9).
(рис.9).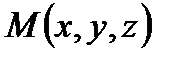 - текущая точка искомой плоскости
- текущая точка искомой плоскости  . Найдем координаты векторов
. Найдем координаты векторов
 .
. принадлежит плоскости
принадлежит плоскости 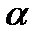 и перпендикулярен вектору
и перпендикулярен вектору 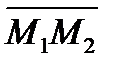 , значит их скалярное произведение
, значит их скалярное произведение 
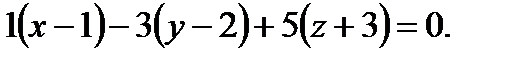
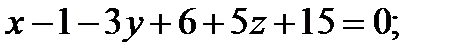
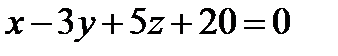 - уравнение плоскости
- уравнение плоскости  .
.
 - (рис.10). Точка
- (рис.10). Точка 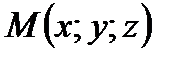 - текущая точка плоскости.
- текущая точка плоскости.
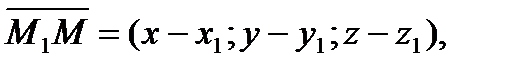 ,
, 
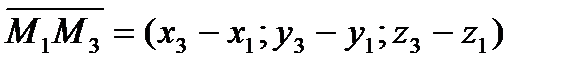

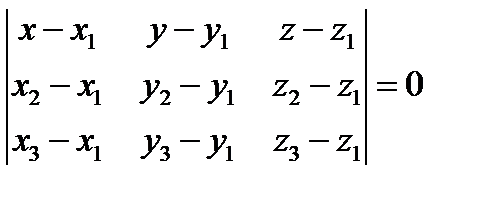 - уравнение плоскости, проходящей
- уравнение плоскости, проходящей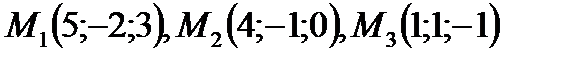 (рис.11).
(рис.11).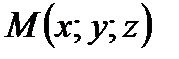 - текущая точка плоскости. Найдем координаты трех компланарных векторов:
- текущая точка плоскости. Найдем координаты трех компланарных векторов:  ,
,  ,
,  .
.
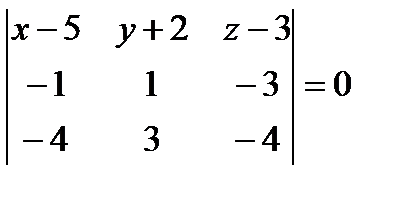
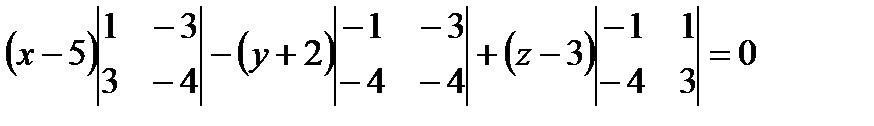
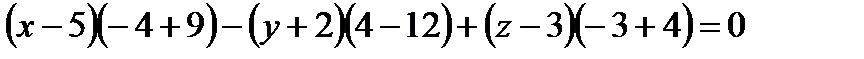
 - уравнение плоскости
- уравнение плоскости 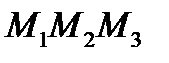 .
. задана общим уравнением
задана общим уравнением 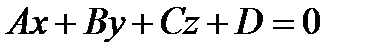 .
. до плоскости
до плоскости  (рис12) вычисляют по формуле
(рис12) вычисляют по формуле 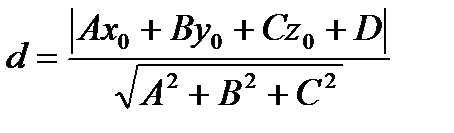 .
.
 до плоскости
до плоскости  .
.  .
.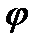 между их векторами нормалей (рис.13).
между их векторами нормалей (рис.13). с нормалью
с нормалью 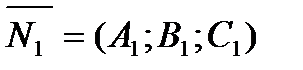
 с нормалью
с нормалью 

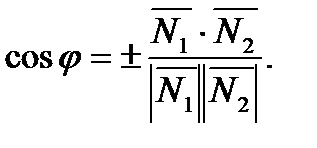
 ;
;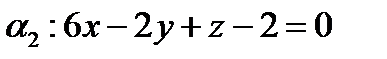 .
.

 Отсюда,
Отсюда,
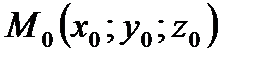 параллельно вектору
параллельно вектору 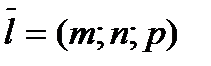 , который называется направляющим вектором прямой а (рис.14).
, который называется направляющим вектором прямой а (рис.14).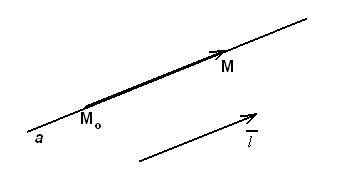
 - текущая точка прямой. Вектор
- текущая точка прямой. Вектор  лежит на прямой и коллинеарен вектору
лежит на прямой и коллинеарен вектору  . Из условия коллинеарности двух векторов, имеем:
. Из условия коллинеарности двух векторов, имеем: 
 , получим параметрические уравнения прямой:
, получим параметрические уравнения прямой: 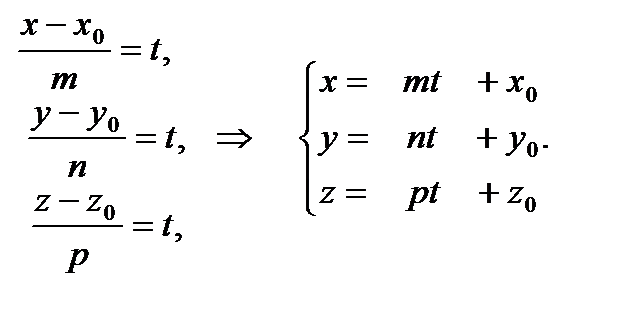
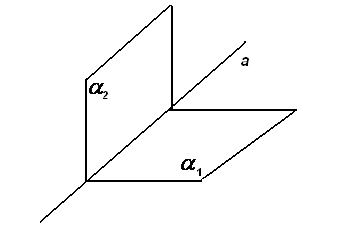
 - общие уравнения прямой в пространстве.
- общие уравнения прямой в пространстве. и
и 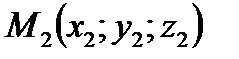 :
: 

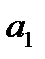 задана общими уравнениями
задана общими уравнениями
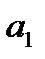 и прямой
и прямой  ,заданной уравнениями
,заданной уравнениями
 , тогда значения других неизвестных находим из системы
, тогда значения других неизвестных находим из системы 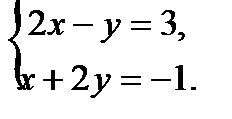
 .
. , через которую проходит искомая прямая. В качестве направляющего вектора прямой можно взять вектор
, через которую проходит искомая прямая. В качестве направляющего вектора прямой можно взять вектор  , где
, где  ,
, 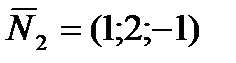 - нормальные векторы плоскостей, линией пересечения которых является прямая. Таким образом,
- нормальные векторы плоскостей, линией пересечения которых является прямая. Таким образом,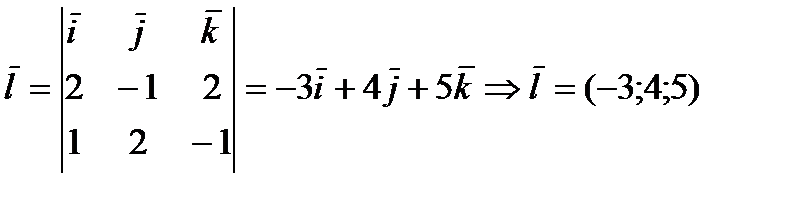 .
.

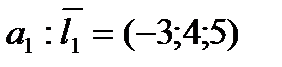 , направляющий вектор прямой
, направляющий вектор прямой 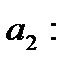
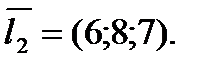 Угол между прямыми
Угол между прямыми  и
и  равен острому углу между их направляющими векторами:
равен острому углу между их направляющими векторами: