Министерство образования и науки
Вычислить: а) C·B ; б) α· Α ;+β· B ; в) А -1
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
21)
22)
23)
24)
25)
26)
27)
28)
29)
30)
Решить систему линейных уравнений по формулам Крамера, матричным методом, методом Гаусса
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30)
Решить системы линейных уравнений методом Гаусса
1) а) б) 2) а) б) 3) а) б) 4) а) б) 5) а) б) 6) а) б) 7) а) б) 8) а) б) 9) а) б) 10) а) б) 11) а) б) 12) а) б) 13) а) б) 14) а) б) 15) а) б) 16) а) б) 17) а) б) 18) а) б) 19) а) б) 20) а) б) 21) а) б) 22) а) б) 23) а) б) 24) а) б) 25) а) б) 26) а) б) 27) а) б) 28) а) б) 29) а) б) 30) а) б)
4 Даны координаты точек
Найти: а) угол между векторами ;
б) площадь треугольника ;
В) высоту треугольника, опущенную из
вершины ;
г) объем пирамиды ;
Д) высоту пирамиды, опущенную из
вершины
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30)
5 Составить уравнение плоскости, проходящей через точку
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30)
6Даны координаты точек
Найти: а) уравнение плоскости, проходящей через
точки ;
б) расстояние от точки ;
В) угол между плоскостью и плоскостью
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) 29) 30)
Прямая a1 задана общими уравнениями .
Найти: а) канонические и параметрические уравнения
прямой a 1 ;
б) найти угол между прямой a 1 2 ,
заданной уравнениями:
1) a1 : 2)a1 : 3) a1 : 4) a1 : 5) a1 : 6) a1 : 7) a1 : 8) a1 : 9) a1 : 10) a1 : 11) a1 : 12) a1 : 13) a1 : 14) a1 : 15) a1 : 16) a1 : 17) a1 : 18) a1 : 19) a1 : 20) a1 : 21) a1 : 22) a1 : 23) a1 : 24) a1 : 25) a1 : 26) a1 : 27) a1 : 28) a1 : 29) a1 : 30) a1 :
Найти угол между прямой и плоскостью ,
Точку пересечения прямой и плоскости
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
21)
22)
23)
24)
25)
26)
27)
28)
29)
30)
9 Даны координаты точек
Найти: а) уравнение медианы ;
б) уравнение высоты ;
в) угол между медианой ;
г) уравнение прямой, проходящей через точку
параллельно прямой
1)
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...
Понятие метода в психологии. Классификация методов психологии и их характеристика Метод – это путь, способ познания, посредством которого познается предмет науки (С...
ЛЕКАРСТВЕННЫЕ ФОРМЫ ДЛЯ ИНЪЕКЦИЙ К лекарственным формам для инъекций относятся водные, спиртовые и масляные растворы, суспензии, эмульсии, новогаленовые препараты, жидкие органопрепараты и жидкие экстракты, а также порошки и таблетки для имплантации...
Тема 5. Организационная структура управления гостиницей 1. Виды организационно – управленческих структур. 2. Организационно – управленческая структура современного ТГК...
Приготовление дезинфицирующего рабочего раствора хлорамина Задача: рассчитать необходимое количество порошка хлорамина для приготовления 5-ти литров 3% раствора...
Дезинфекция предметов ухода, инструментов однократного и многократного использования
Дезинфекция изделий медицинского назначения проводится с целью уничтожения патогенных и условно-патогенных микроорганизмов - вирусов (в т...
Машины и механизмы для нарезки овощей В зависимости от назначения овощерезательные машины подразделяются на две группы: машины для нарезки сырых и вареных овощей...

 α=3; β=5;
α=3; β=5; α=-4; β=6;
α=-4; β=6; α=8; β=-2;
α=8; β=-2; α=2; β=3;
α=2; β=3; α=-2; β=-2;
α=-2; β=-2; α=-3; β=-2;
α=-3; β=-2; α=5; β=-2;
α=5; β=-2; α=-2; β=-3;
α=-2; β=-3; α=-3; β=3;
α=-3; β=3; α=5; β=2;
α=5; β=2; α=-4; β=2;
α=-4; β=2; α=-4; β=-6;
α=-4; β=-6; α=-3; β=2;
α=-3; β=2; α=-3; β=2;
α=-3; β=2; α=-4; β=3;
α=-4; β=3; α=3; β=-4;
α=3; β=-4; α=2; β=5;
α=2; β=5; α=-5; β=-5;
α=-5; β=-5; α=2; β=-3;
α=2; β=-3;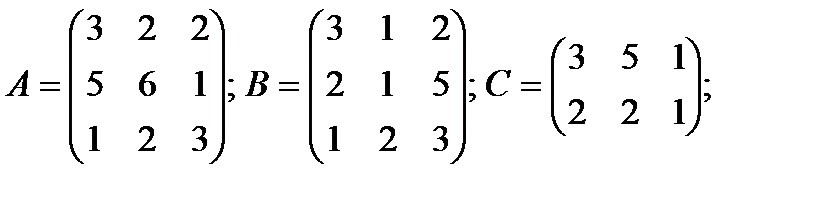 α=3; β=-2;
α=3; β=-2; α=-3; β=4;
α=-3; β=4; α=5; β=4;
α=5; β=4; α=-2; β=-3;
α=-2; β=-3; α=2; β=3;
α=2; β=3; α=-3; β=2;
α=-3; β=2; α=3; β=4;
α=3; β=4;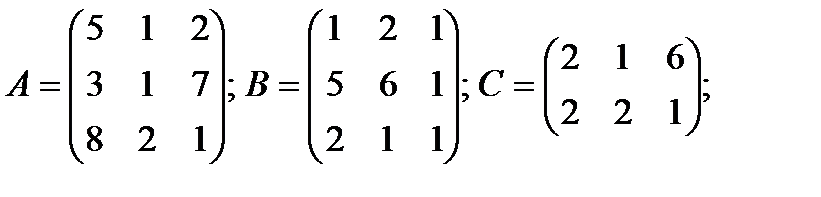 α=-3; β=2;
α=-3; β=2; α=3; β=4;
α=3; β=4; α=-5; β=-2;
α=-5; β=-2; α=-4; β=2.
α=-4; β=2. ;
;
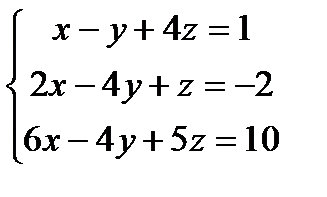 ;
;
 ;
;
 ;
;
 ;
;
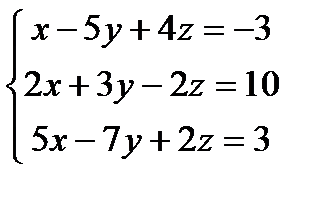 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
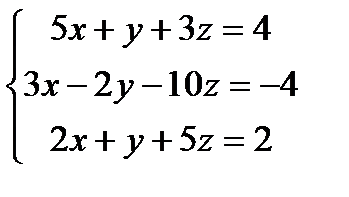 ;
;
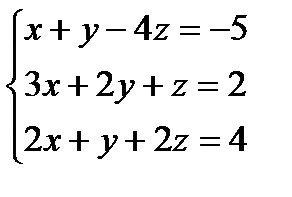 ;
;
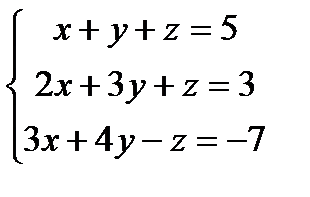 ;
;
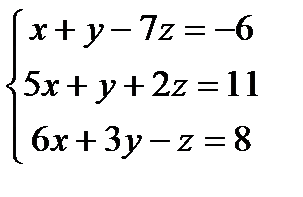 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
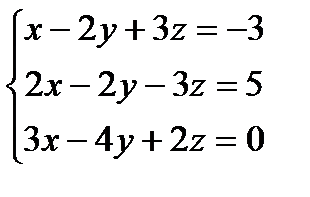 ;
;
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
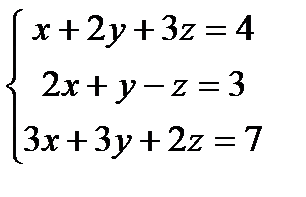 ;
;
 ;
;
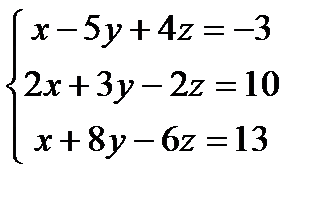 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
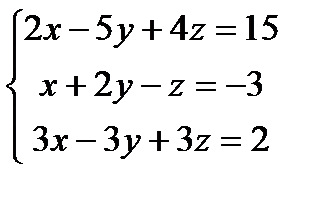 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
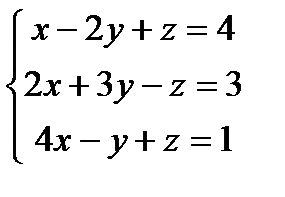 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
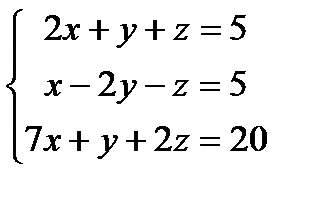 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
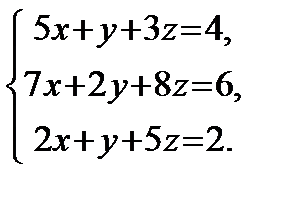 ;
;
 ;
;
 ;
;
 ;
;
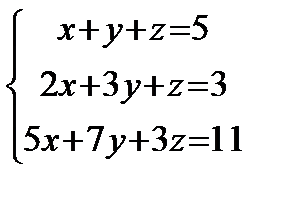 ;
;
 ;
;
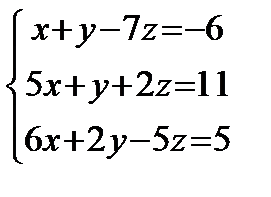 ;
;
 ;
;
 ;
;
 ;
;
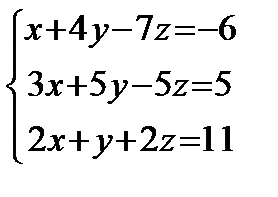 ;
;
 ;
;
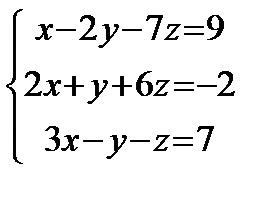 ;
;
 ;
;
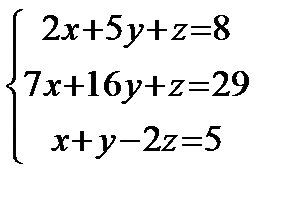 ;
;
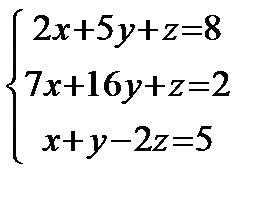 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.

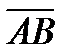 и
и  ;
; ;
;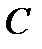 на сторону
на сторону  ;
; ;
;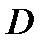 на основание
на основание 
 ;
;
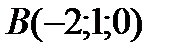 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
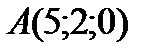 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
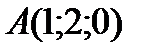 ;
;
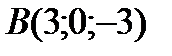 ;
;
 ;
;
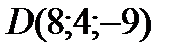 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
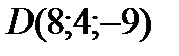 ;
;
 ;
;
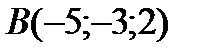 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
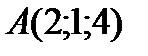 ;
;
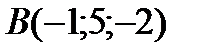 ;
;
 ;
;
 ;
;
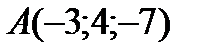 ;
;
 ;
;
 ;
;
 ;
;
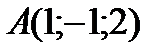 ;
;
 ;
;
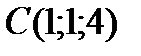 ;
;
 ;
;
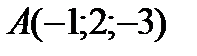 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
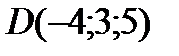 ;
;
 ;
;
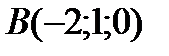 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
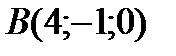 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
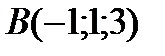 ;
;
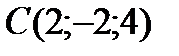 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 и перпендикулярно вектору
и перпендикулярно вектору 
 ;
;
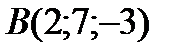 ;
;
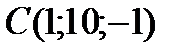 ;
;
 ;
;
 ;
;
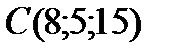 ;
;
 ;
;
 ;
;
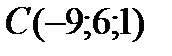 ;
;
 ;
;
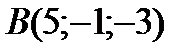 ;
;
 ;
;
 ;
;
 ;
;
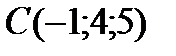 ;
;
 ;
;
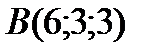 ;
;
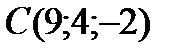 ;
;
 ;
;
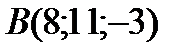 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
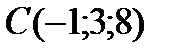 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
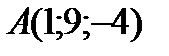 ;
;
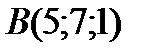 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
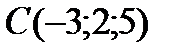 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
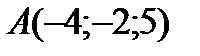 ;
;
 ;
;
 ;
;
 ;
;
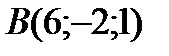 ;
;
 ;
;
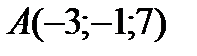 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
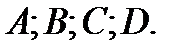
 ;
;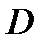 до плоскости
до плоскости 
 ;
;
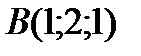 ;
;
 ;
;
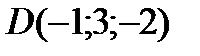 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
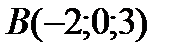 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
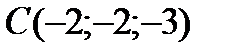 ;
;
 ;
;
 ;
;
 ;
;
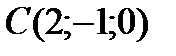 ;
;
 ;
;
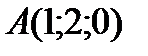 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
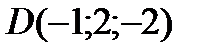 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
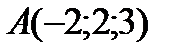 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
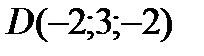 ;
;
 ;
;
 ;
;
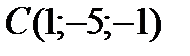 ;
;
 ;
;
 ;
;
 ;
;
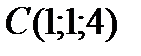 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
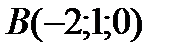 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
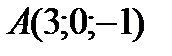 ;
;
 ;
;
 ;
;
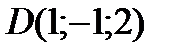 ;
;
 ;
;
 ;
;
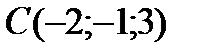 ;
;
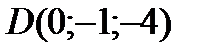 ;
;
 ;
;
 ;
;
 ;
;
 .
.

 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
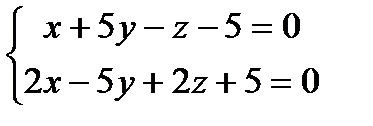 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
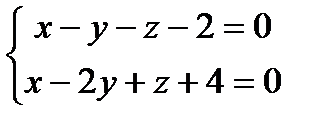 ;
;
 ;
;
 ;
;
 ;
;
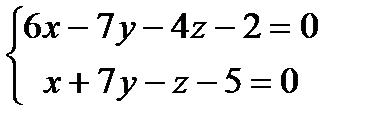 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
;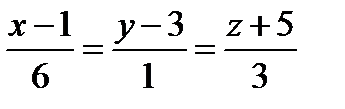 ,
,  ;
;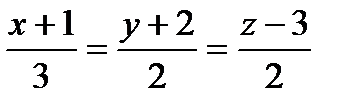 ,
,  ;
; ,
, 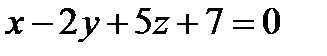 ;
;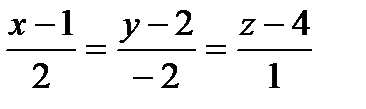 ,
, 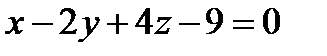 ;
; ,
,  ;
; ,
,  ;
; ,
, 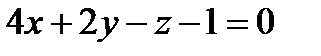 ;
; ,
,  ;
;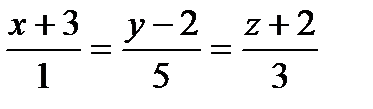 ,
,  ;
; ,
,  ;
;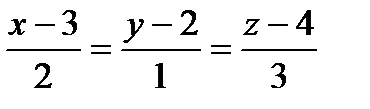 ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
, 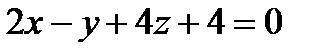 ;
; ,
,  ;
; ,
, 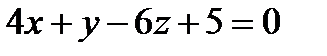 ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
, 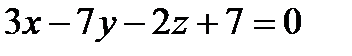 ;
;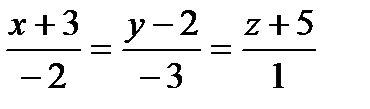 ,
,  .
.
 ;
; ;
;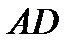 и высотой
и высотой 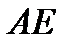 ;
;

 ,
, 



