Обратные матрицы
Квадратная матрица Условием существования матрицы Алгебраическим дополнением имеет следующие алгебраические дополнения:
Если квадратная матрица
Задача. Решить систему уравнений матричным способом:
Решение. Составим матрицы:
Тогда матричная запись рассматриваемой системы уравнений будет иметь вид где обратная матрица Найдем определитель матрицы
Алгебраические дополнения
Обратная матрица Решение матричного уравнения:
Ответ:
Задача. Решить систему уравнений методом Крамера:
Решение. Из предыдущей задачи главный определитель системы Найдём определитель
Найдём определитель
Аналогично:
По формулам Крамера решение системы:
Ответ:
Задача. Решить систему уравнений методом Гаусса:
Решение. Составим расширенную матрицу системы: слева от черты коэффициенты при неизвестных, справа свободные члены. Приведем расширенную матрицу системы с помощью элементарных преобразований со строками к виду: Обозначим строки матрицы через Элементарные преобразования строк следующие: 1.Поменять местами строки 2.Строку разделить или умножить на число 3.Линейная комбинация строк Тогда,
Из третьей строки последней матрицы находим: Из второй строки находим: Из первой строки находим: Ответ:
Задача. Решить систему уравнений методом Гаусса:
Решение. Составим расширенную матрицу системы:
Из третьей строки последней матрицы: Из второй строки имеем Из первой строки находим: Ответ:
Задача. Решить систему уравнений методом Гаусса:
Решение. Составим расширенную матрицу из коэффициентов матрицы:
Из последней строки находим
Ответ: система не имеет решений (несовместная система).
|

 называется обратимой, если существует матрица
называется обратимой, если существует матрица  такая, что
такая, что 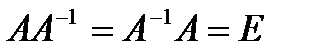 . Эту матрицу называют обратной к матрице
. Эту матрицу называют обратной к матрице 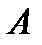 и обозначают
и обозначают  .
.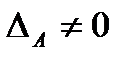 , где
, где  - определитель, составленный из элементов матрицы
- определитель, составленный из элементов матрицы  ).
). элемента матрицы
элемента матрицы  называется произведение числа
называется произведение числа  на минор
на минор 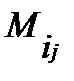 - определитель, получающийся при вычеркиванием
- определитель, получающийся при вычеркиванием  -ой строки и
-ой строки и 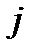 -го столбца. Например, некоторые элементы матрицы
-го столбца. Например, некоторые элементы матрицы 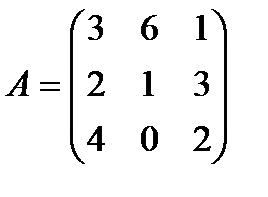
 ;
;  ;
;  ;
; 
 - не вырождена, то обратная матрица
- не вырождена, то обратная матрица  .
.
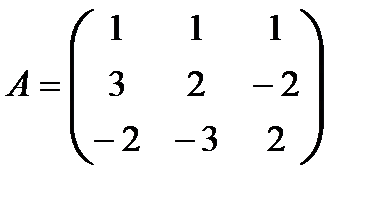 - матрица коэффициентов при неизвестных;
- матрица коэффициентов при неизвестных;  - матрица неизвестных;
- матрица неизвестных; - матрица свободных членов.
- матрица свободных членов.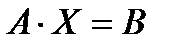 . Решение матричного уравнения
. Решение матричного уравнения 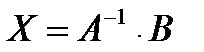 ,
,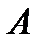 :
: .
.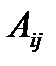 :
: ;
;  ;
;  ;
; ;
;  ;
;  ;
; ;
;  ;
; 
 .
. .
.
 .
. , который получается из определителя
, который получается из определителя  заменой первого столбца столбцом свободных членов.
заменой первого столбца столбцом свободных членов.

 .
.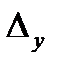 , который получается из определителя
, который получается из определителя  заменой второго столбца столбцом свободных членов, тогда
заменой второго столбца столбцом свободных членов, тогда



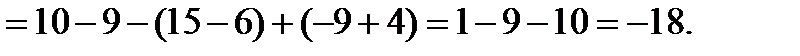
 ,
,  ,
, 



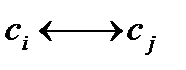 .
.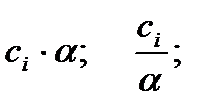

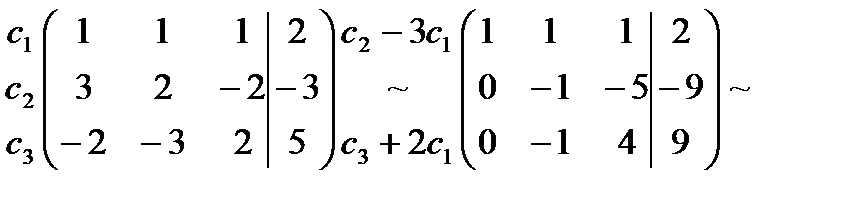


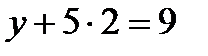 , откуда
, откуда 
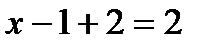 , откуда
, откуда 

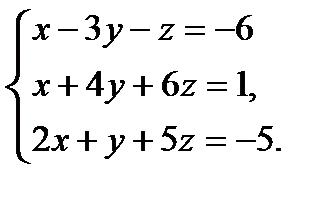


 Откуда,
Откуда, 
 Откуда,
Откуда, 
 Система имеет бесконечное множество решений (совместная неопределенная система).
Система имеет бесконечное множество решений (совместная неопределенная система).
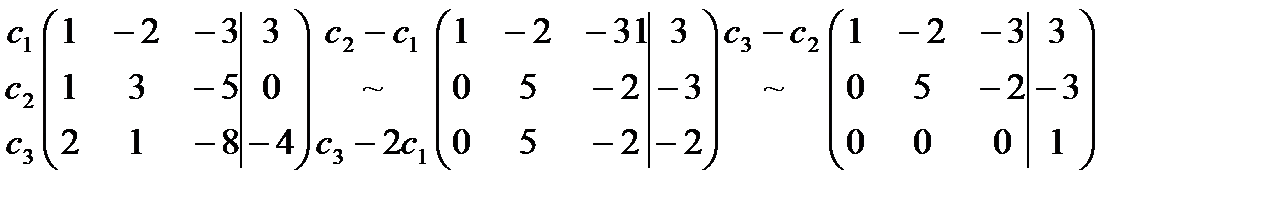
 . Так как деление на ноль невозможно, то данная система не имеет решений.
. Так как деление на ноль невозможно, то данная система не имеет решений.


