Скалярное, векторное и смешанное произведения векторов
Скалярным произведением
Рис.4 Пусть заданы два вектора в координатной форме Скалярное произведение двух ненулевых векторов в координатной форме равно сумме произведений соответствующих координат этих векторов: Косинус угла между векторами вычисляется по формуле: Условием перпендикулярности ненулевых векторов
Векторным произведением двух векторов 1) имеет модуль, численно равный площади параллелограмма, построенного на векторах 2) перпендикулярен к плоскости этого параллелограмма; 3) направлен в такую сторону, с которой кратчайший поворот от
Рис.5
Векторное произведение ненулевых векторов следующим образом: Равенство нулю векторного произведения двух ненулевых векторов является условием их коллинеарности, т.е.
Смешанное произведение трех векторов Смешанное произведение трех векторов вычисляется в координатной форме по формуле:
Равенство нулю смешанного произведения трех ненулевых векторов является условием их компланарности:
Задача. Определить внутренние углы Решение. Внутренний угол
Координаты векторов:
Отсюда, Аналогично, находя предварительно
Отсюда Задача. Вычислить площадь треугольника с вершинами в точках
|

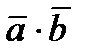 двух ненулевых векторов
двух ненулевых векторов 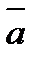 и
и 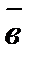 называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними:  , где
, где 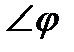 - угол между векторами
- угол между векторами 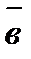 (рис.4).
(рис.4).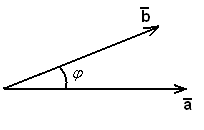
 и
и 
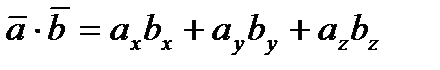 .
. .
.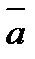 и
и 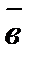 является равенство нулю их скалярного произведения:
является равенство нулю их скалярного произведения: .
.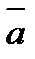 и
и  называется вектор
называется вектор  , который:
, который: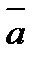 и
и 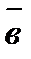 :
: 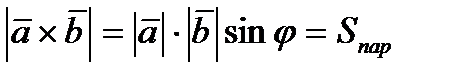 ;
; к
к 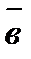 рассматривается совершающимся против часовой стрелки (такое расположение векторов
рассматривается совершающимся против часовой стрелки (такое расположение векторов 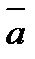 ,
, 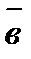 и
и  называется правой тройкой векторов) (рис.5).
называется правой тройкой векторов) (рис.5).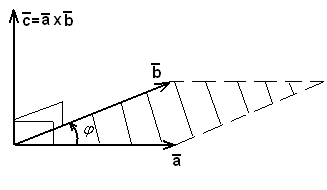
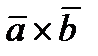 вычисляется через координаты данных векторов
вычисляется через координаты данных векторов 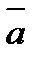 и
и 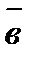

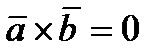

 ½½
½½ 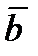 .
.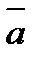 ,
, 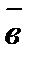 и
и 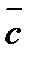 , которое обозначается
, которое обозначается 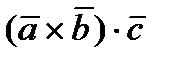 или
или 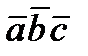 , есть скаляр, абсолютная величина которого равна объему параллелепипеда, построенного на векторах
, есть скаляр, абсолютная величина которого равна объему параллелепипеда, построенного на векторах  ,
, 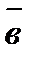 и
и 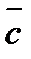 , как на ребрах.
, как на ребрах. .
.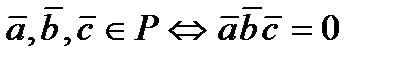 .
. и
и 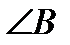 треугольника
треугольника 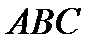 c вершинами в точках
c вершинами в точках 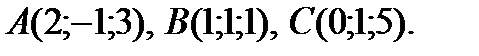
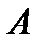 - это угол между векторами
- это угол между векторами 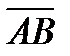 и
и  , который вычисляется через скалярное произведение векторов по формуле:
, который вычисляется через скалярное произведение векторов по формуле: 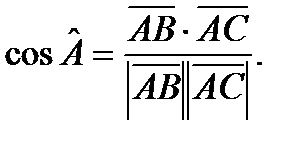
 .
.
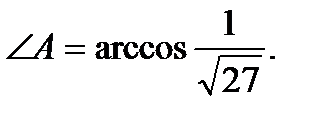
 , получим
, получим

 и высоту
и высоту  (рис.6).
(рис.6).


