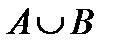Задание №1
Задание №1 Доказать равенство множеств: а) исходя из определения равенства множеств; б) Преобразуя левую (или правую) часть равенства в правую часть (соответственно, в левую); в) используя характеристические функции и представляя множества с помощью булевых векторов.
1.6. (A Решение: а) Пусть Предположим что равенство верно. Тогда Таким образом, заключаем, что равенство неверно.
б) Преобразуем правую часть равенства, используя законы алгебры логики
Следовательно, исходное равенство неверно, так как
в) Построим таблицы истинности для правой и левой частей
Для левой части
Для правой части
Как можно увидеть, последние столбцы в таблицах истинности не совпадают, следовательно, равенство неверно.
|

 B)
B)  (C
(C  . Тогда имеем: либо
. Тогда имеем: либо  , либо
, либо  . Если
. Если 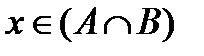 , то
, то  и одновременно
и одновременно  , если же
, если же 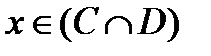 , то
, то  и одновременно
и одновременно 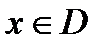 .
. . Это означает, что
. Это означает, что  , либо
, либо  , либо
, либо  , либо
, либо  . Значит x одновременно содержится либо в A и C, либо, B и C, либо A и D, либо B и D. Но исходя из первой части доказательства этого не может быть (x может одновременно содержаться либо в A и B, либо в C и D).
. Значит x одновременно содержится либо в A и C, либо, B и C, либо A и D, либо B и D. Но исходя из первой части доказательства этого не может быть (x может одновременно содержаться либо в A и B, либо в C и D).