Задание №2на множестве А(в каждом варианте А – конкретное множество) задано бинарное отношение
2.6. а) А – множество действительных чисел и для любых x, y б) А – множество положительных действительных чисел и для любых x, y
Решение: а) По определению рациональных чисел имеем:
Исследуем свойства бинарного отношения
Отношение антирефлексивно: поскольку
Отношение симметрично: поскольку Если
Отношение транзитивно: поскольку Поскольку
При сложении двух рациональных чисел получим рациональное число, поэтому
б) Исследуем свойства бинарного отношения
Отношение рефлексивно: поскольку
Отношение антисимметрично: поскольку
Отношение транзитивно: поскольку
|
. Какими из свойств (рефлективность, симметричность, транзитивность и т.д.) оно обладает?
А имеем 
- рациональное число.
.
, 
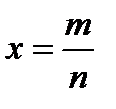, где 
, 
множество целых чисел, 
множество натуральных чисел
, то есть
- целое число
, то есть
- рациональное число, то 
- также рациональное число (только с противоположным знаком)
, то есть
- рациональное число, 
- рациональное число. А, как известно, сумма 2-х рациональных чисел есть число рациональное, то получим:
- рациональное число
, то есть 
(
)
, то есть одновременное выполнение неравенств 
и 
возможно только в случае 
