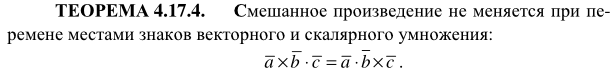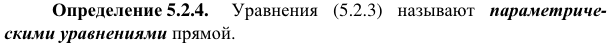Основные свойства непрерывных функций
38. Свойства функции непрерывных на отрезках
Определение производной функции в точке
Дифференциал функции. Правила дифференцирования.
Производная сложной функции. Производная обратной функции.
Таблица производных
Бесконечная производная, односторонние производные.
Производная функции, заданной неявно.
Производная функции, заданной параметрически.
46. Логарифмическая производная
47. Производные высших порядков
48 применение дифференциала в приближ-х вычисл-х 49 инвариантность формы дифференциала. 51,53 некоторые теоремы о дифф-мых ф-ях
54 Применение производной.Правило Лопиталя – Бернулли
55 исследование поведения ф-ции на лок-ный экстремум 56 выпуклость вогнутость. Т перегиба
57 ассимптоты
58 общая схема исследования ф-ции 59 глобальный экстремум ф-ции. Практич-е задачи на оптимизацию. Схема постр-я математич-й модели
Основные понятия векторной алгебры Определение 4.1. 1. Величины, для задания которых достаточно указать только их численное значение, называются скалярными величи- нами. Определение 4.1.2. Величины, для задания которых необходимо указать не только числовое значение, но и направление, называются век - торными величинами Определение 4.1.3. Связным (геометрическим) вектором назы- вают направленный отрезок прямой. Термин «вектор» ввел Гамильтон (около 1845 г.) Определение 4.1.4. Длиной вектора называют расстояние между его началом и концом. Длина вектора называется модулем. Связный вектор полностью определяется: - точкой приложения,- направлением,- длиной. Определение 4.1.5. Направленный отрезок, рассматриваемый с точностью до выбора его начала, называют свободным вектором. Определение 4.1.6. Вектор называется нулевым или нуль - вектором, если его длина равна нулю. Нулевой вектор не имеет определенного на- правления. Определение 4.1.7. Вектор, длина которого равна единице, назы- вается единичным. Определение 4.1.8. Векторы, лежащие на одной или на парал- лельных прямых называют коллинеарными. Определение 4.1.9. Коллинеарные векторы, которые имеют одно и то же направление, называются сонаправленными и обозначаются: a -- b. Коллинеарные векторы, имеющие противоположное направление, называются противонаправленными и обозначаются: a ¯ b. Определение 4.1.10. Единичный вектор, сонаправленный с векто- ром a, называют его ортом a 0. Определение 4.1.11. Векторы называются равными, если они име- ют одинаковую длину и направление. Определение 4.1.12. Вектор - a противоположен вектору a, если он имеет длину вектора a, но противоположное направление. Определение 4.1.13. Векторы, лежащие в одной или параллельных плоскостях, называются компланарными. 64 Линейные операции над векторами
Определение 4.2.2. Суммой векторов называется вектор c, начало которого совпадает с началом первого, а конец – с концом последнего,при условии, что точка приложения каждого последующего вектора совпадает с концом предыдущего. Определение 4.2.3. Разностью векторов a и b называют такой вектор, c равный a - b, который нужно сложить с вектором b, чтобы по- лучить вектор a: c = a - b; c + b = a. 65 прекция вектора на ось
66 линейная зависимость векторов. Базис. Координаты вектора. Определение 4.5.2. Система векторов образует базис некоторого пространства, если:1) система линейно независима;2) любой вектор данного пространства можно представить в виде линейной комбинации векторов данной системы. Определение 4.5.4. Пусть в некотором пространстве задана точка O. Совокупность точки и некоторого базиса называют системой координат. Точку O называют началом координат. Определение 4.5.5. Если длины базисных векторов равны единице, то базис называется нормированным. Определение 4.5.6. Если все векторы базиса взаимно перпендикулярны, то базис называют ортогональным. Определение 4.5.7. Базис, у которого базисные векторы нормированы и ортогональны, называют ортонормированным. Определение 4.5.8. Система координат с ортонормированным базисом называется декартовой прямоугольной системой координат. Сокращенно - ДПСК. ТЕОРЕМА 4.8.1. Два вектора равны тогда и только тогда, когда равны их соответствующие координаты. 67 Скалярное произведение двух векторов и его св-ва
Определение 4.11.1. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. свойства 69. Векторным произведением векторов a и b называется вектор c, удовлетворяющий следующим условиям:
Алгебраические свойства векторного произведения ТЕОРЕМА Векторное произведение антикоммутативно, т.е.
71. Смешанное произведение векторов
73. Собственные значения и собственные векторы матриц
74. алгебраические линии. прямая на пл-ти-линия 1го порядка
75. Способы задания прямой на плоскости (точка и вектор нормали).
76. Способы задания прямой на плоскости (точка и направляющий вектор).
77. Способы задания прямой на плоскости (две точки).
78. Угол между прямыми на плоскости.
79 взаимное расположение прямых на плоскости
80 расстояние от точки до прямой на пл-ти 81 Алгебр-е линии 2го порядка 82 Элипс, Важные хар-ки элипса Ур-е эллипса 83. Гипербола. Канонические ур-я гиперболы Определение 5.6.1. Гиперболой называется геометрическое место точек, модуль разности расстояний от которых до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная (ее обозначают через 2а), причем, эта постоянная меньшая, чем расстояние между фокусами. Определение 5.6.2. Ось, на которой находятся вершины гиперболы называется действительной. Ось, на которой нет вершин, называется мнимой. 84 важные хар-ки
85 парабола. Каноническое ур-е параболы.
86 ур-я пов-ти и линии в пространстве. Плоскость-алгебр-я пов-ть в простр-ве 87 Способы задания плоскости(точка и вектор нормали) (*)88-89 способы задания пл-ти 1(точка и 2напр-х в-ра),2(2точки и напр-й в-р)
91 Уравнение плоскости в отрезках.
92 Взаимное расположение плоскостей. 93Способы задания прямой в пространстве. 95Взаимное расположение прямых в пространстве. 96Взаимное расположение прямой и плоскости в пространстве.
97 поверхности второго порядка. Метод сечений
|